Loading [MathJax]/jax/output/HTML-CSS/jax.js
+ - 0:00:00
Notes for current slide
Notes for next slide

1.3 — Sequential Games

ECON 316 • Game Theory • Fall 2021

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/gameF21
gameF21.classes.ryansafner.com

Outline

Games in Extensive Form

Mover Advantages

How Reasonable is Rollback Thinking?

The Century Mark Game

Rules: Two (teams of) players alternating turns

  • The count starts at 0
    1. Team 1 adds a number 1-10 to the tally
    2. Team 2 adds a number 1-10 to the tally
  • The first team to bring the tally to 100 wins

Sequential Games with Perfect Information

  • Strict order of play

  • Perfect information

    • No external uncertainty: nature/probability does not interfere between choices → outcomes
    • No strategic uncertainty: each player observes the history of other players’ moves

  • Can be represented in extensive form, i.e. a game tree

Games in Extensive Form

Games in Extensive Form

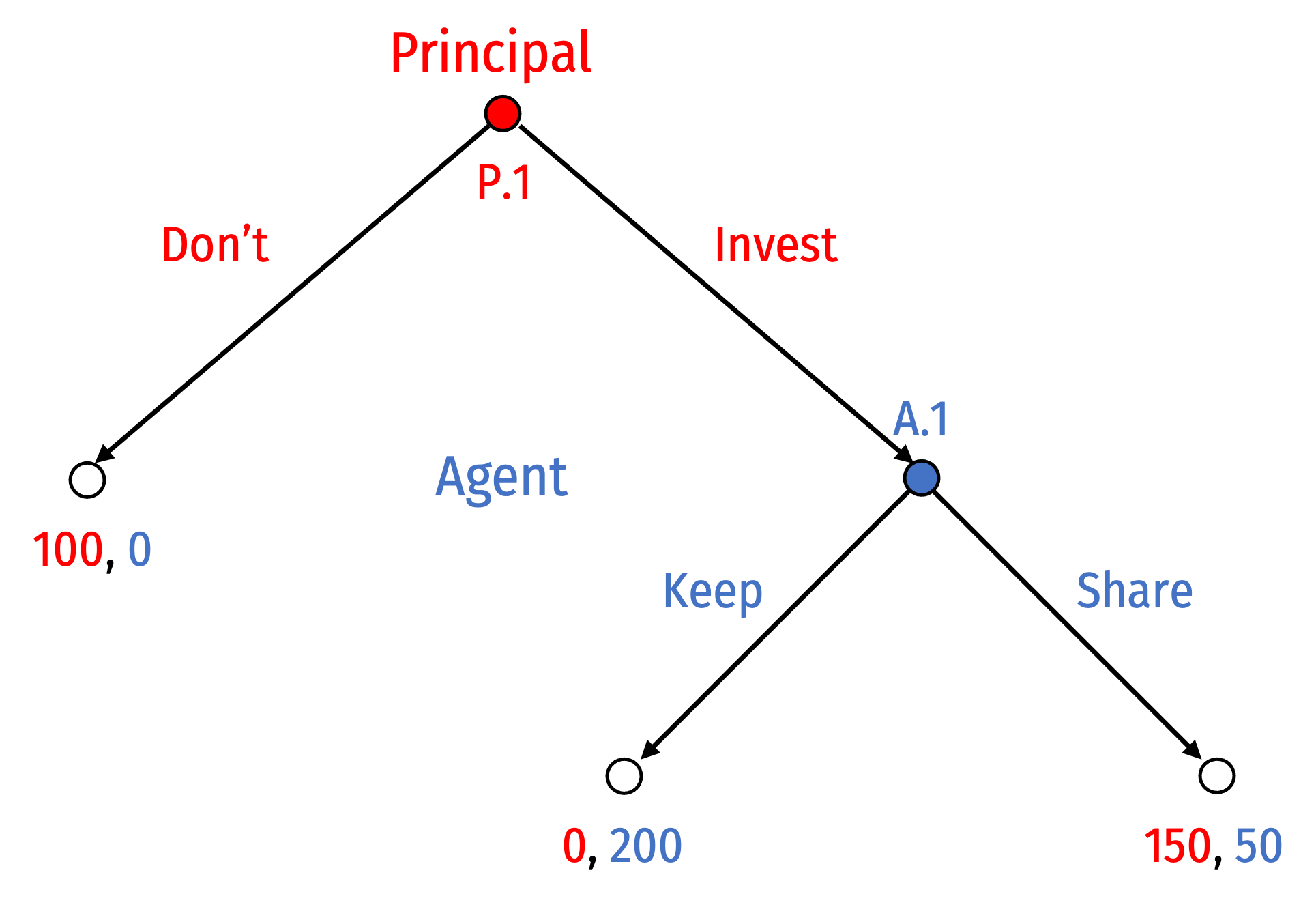
  • Example: “trust” game

  • Principal starts with $100. If they invest, with Agent, it doubles to $200

  • Agent then decides whether to share or keep it

Games in Extensive Form

  • Example: “trust” game

  1. Principal (Player 1) moves first.

  2. Agent (Player 2) moves second (but only if Principal has played Invest).

  • The game ends.

Games in Extensive Form

  • Designing a game tree:

  • Decision nodes: decision point for each player

    • Solid nodes, I've labeled and color-coded by player (P.1, A.1)

  • Terminal nodes: outcome of game, with payoff for each player

    • Hollow nodes, no further choices

Games in Extensive Form: Outcomes

  • Three possible outcomes:
  1. (Don't): 100, 0
  2. (Invest, Keep): 0, 200
  3. (Invest, Share): 150, 50

Strategies

  • (“Pure”) strategy: a player’s complete plan of action for every possible contingency

    • i.e. what player will choose at every possible decision node, even if it’s never reached

  • Think of a strategy like an algorithm:

If we reach node 1, then I will play X; if we reach node 2, then I will play Y; if...

Trust Game: Strategies

  • Principal has 2 possible strategies:

    1. Don't at P.1
    2. Invest at P.1

  • Agent has 2 possible strategies:

    1. Keep at A.1
    2. Share at A.1

  • Note Agent's strategy only comes into play if Principal plays Invest and the game reaches node A.1

Solving the Game: Backward Induction

  • Solve a sequential game by “backward induction” or “rollback”

  • To determine the outcome of the game, start with the last-mover (i.e. decision nodes just before terminal nodes) and work to the beginning

  • A process of considering “sequential rationality”:

“If I play X, my opponent will respond with Y; given their response, do I really want to play X?”

  • What is that mover's best choice to maximize their payoff?

Solving the Game: Backward Induction

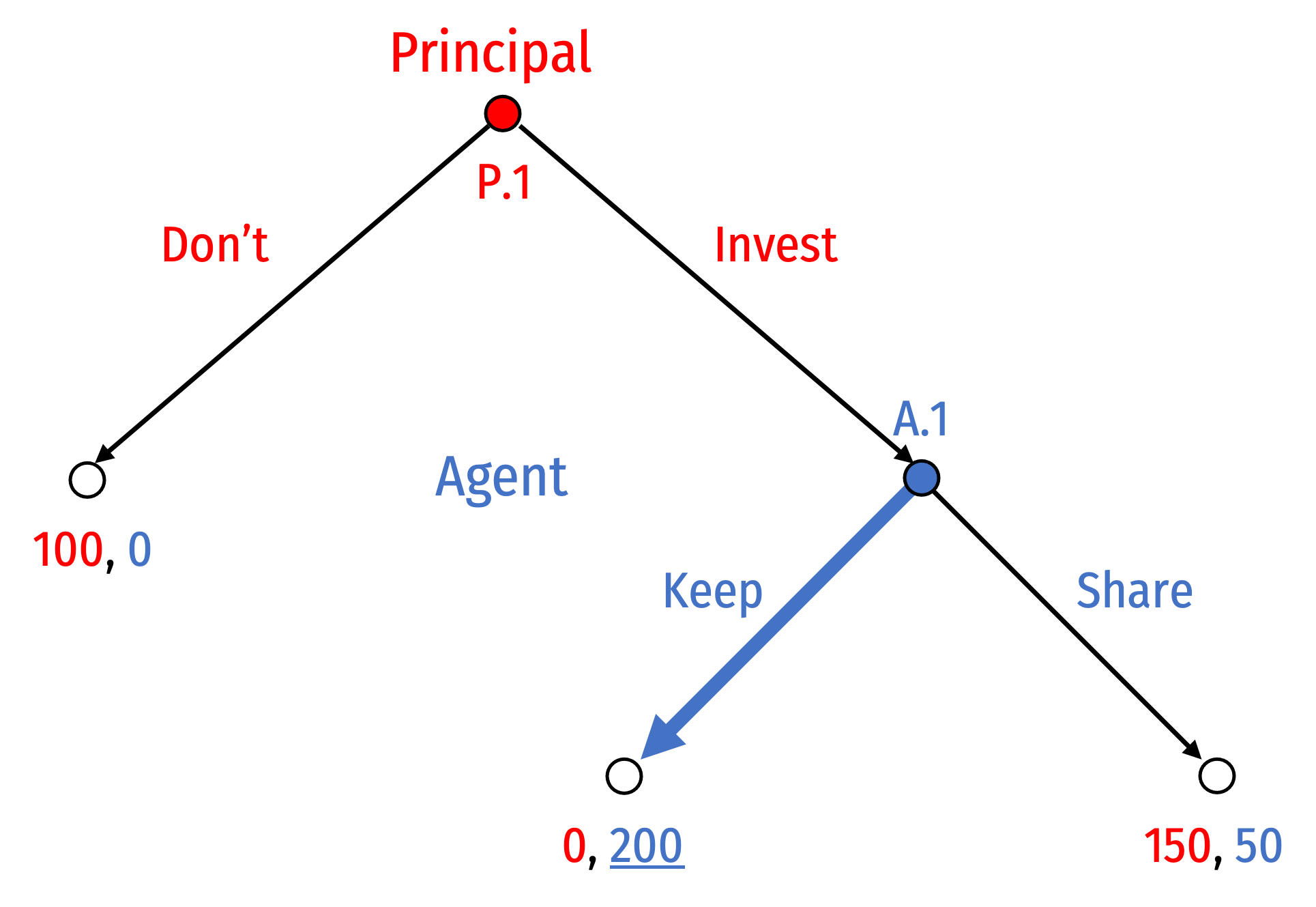
  • We start at A.1 where Agent can:
    • Keep to yield outcome (0, 200)
    • Share to yield outcome (150, 50)

Solving the Game: Backward Induction

  • We start at A.1 where Agent can:

    • Keep to yield outcome (0, 200)
    • Share to yield outcome (150, 50)

  • Agent only considers their own payoff

    • (Invest, Keep) ≻ (Invest, Share)
    • 200 ≻ 50

Solving the Game: Backward Induction

  • Agent will Keep if the game reaches node A.1

  • Recognizing this, what will Principal do?

Solving the Game: Backward Induction

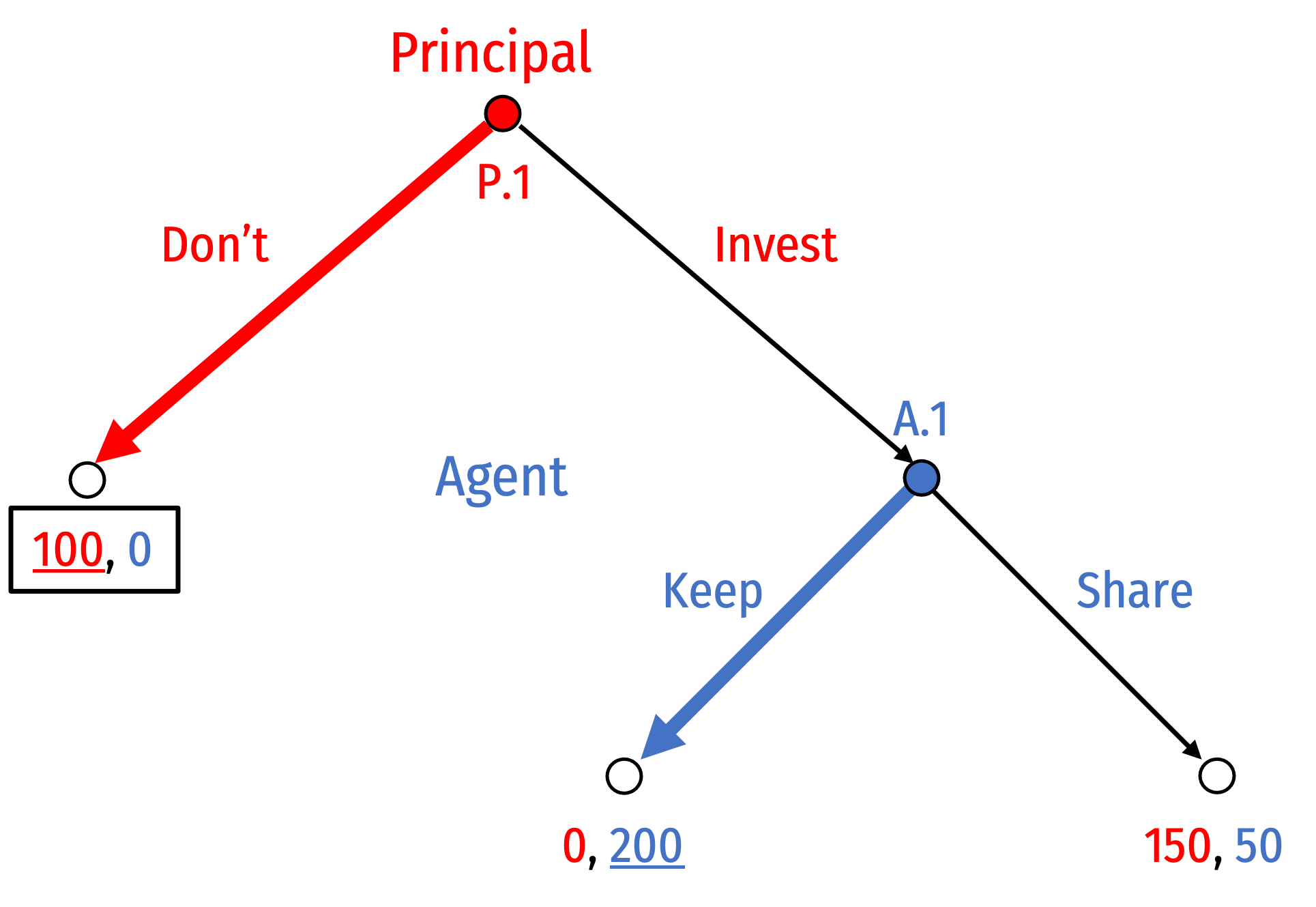
  • Work our way up to P.1 where Principal can:

    • Don't to yield outcome (100, 0)
    • Invest, knowing Agent will Keep, to yield outcome (0, 200)

  • Principal only considers their own payoff

    • (Don't) ≻ (Invest, Keep)
    • 100 ≻ 0

Solving the Game: Backward Induction

  • Equilibrium: (Don't, Keep)
    • Defined by the strategy played by each player

Solving the Game: Pruning the Tree

  • As we work backwards, we can prune the branches of the game tree

    • Highlight branches that players will choose
    • Cross out branches that players will not choose

  • Equilibrium path of play is highlighted from the root to one terminal node

    • (Don't)
    • All other paths are not taken

Another Example: Senate Race

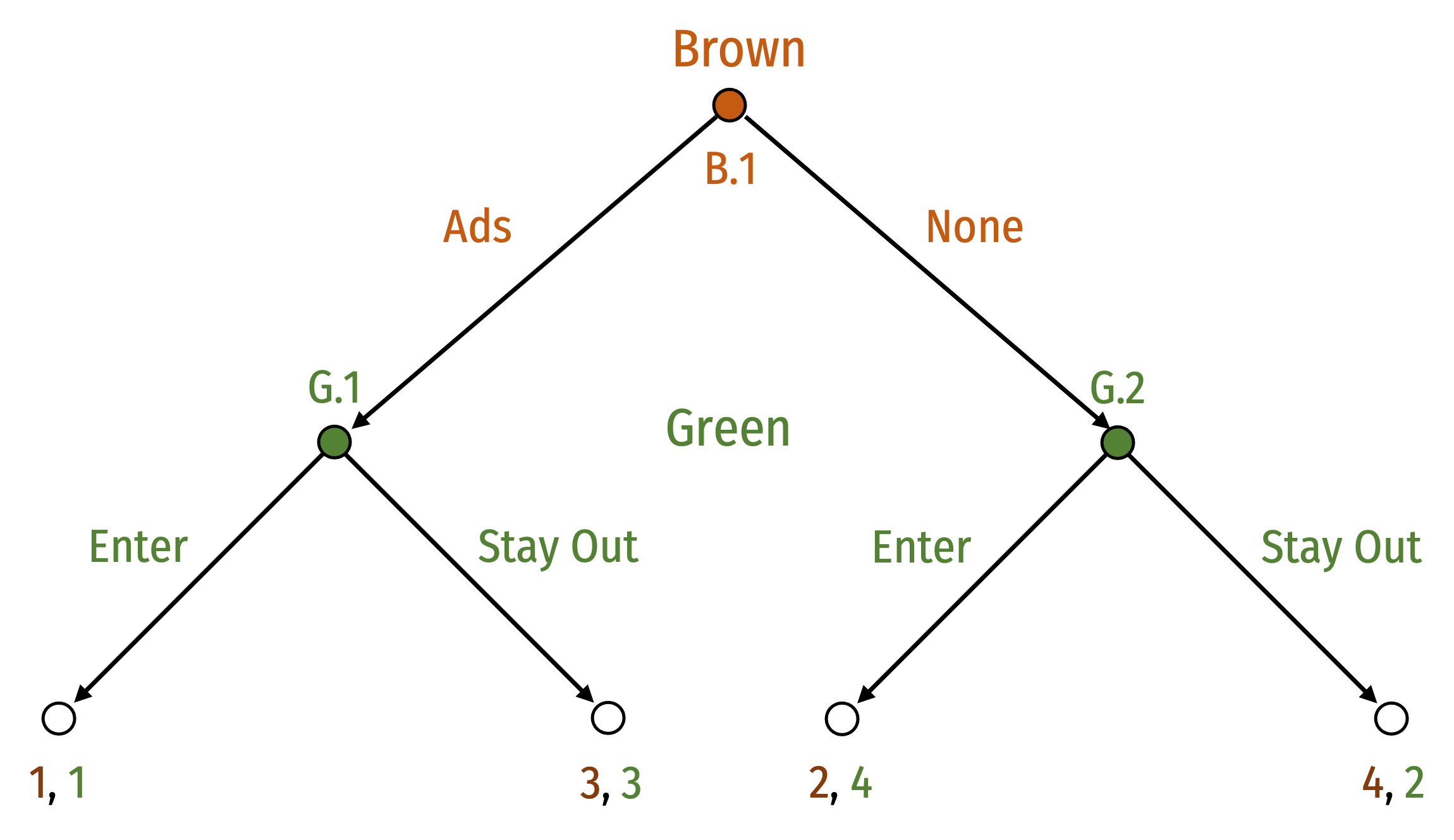
  • Incumbent Senator Brown runs for reelection

  • Challenger is Congresswoman Green

  • Brown moves first, must decide early-on to Run Ads or No Ads

  • Green moves second, must decide to Enter or Stay Out

Another Example: Senate Race

  • Payoff considerations:

    • Ads are costly, Brown would prefer to not run ads
    • Green will fare better if Brown does not run ads

  • Use 1,2,3,4 for simple rankings

Senate Race Game: Strategies

  • Brown has 2 strategies:
    1. Ads at B.1
    2. None at B.1

Senate Race Game: Strategies

  • Green has 4 strategies:

  • Two decision nodes, two strategies at each node, hence 22=4

    1. Enter at G.1; Enter at G.2
    2. Enter at G.1; Stay Out at G.2
    3. Stay Out at G.1; Enter at G.2
    4. Stay Out at G.1; Stay Out at G.2

Senate Race Game: Strategies

  • Remember, think about a strategy like an algorithm
    1. If Ads then Enter; if None then Enter (always Enter)
    2. If Ads then Enter; if None then Stay Out
    3. If Ads then Stay Out; if None then Enter
    4. If Ads then Stay Out; if Stay Out then Stay Out (always Stay Out)

Senate Race Game: Solution

  • To apply backward induction, begin with the last-mover
  1. What will Green choose...
    • If Brown were to run Ads?
    • If Brown were to run None?

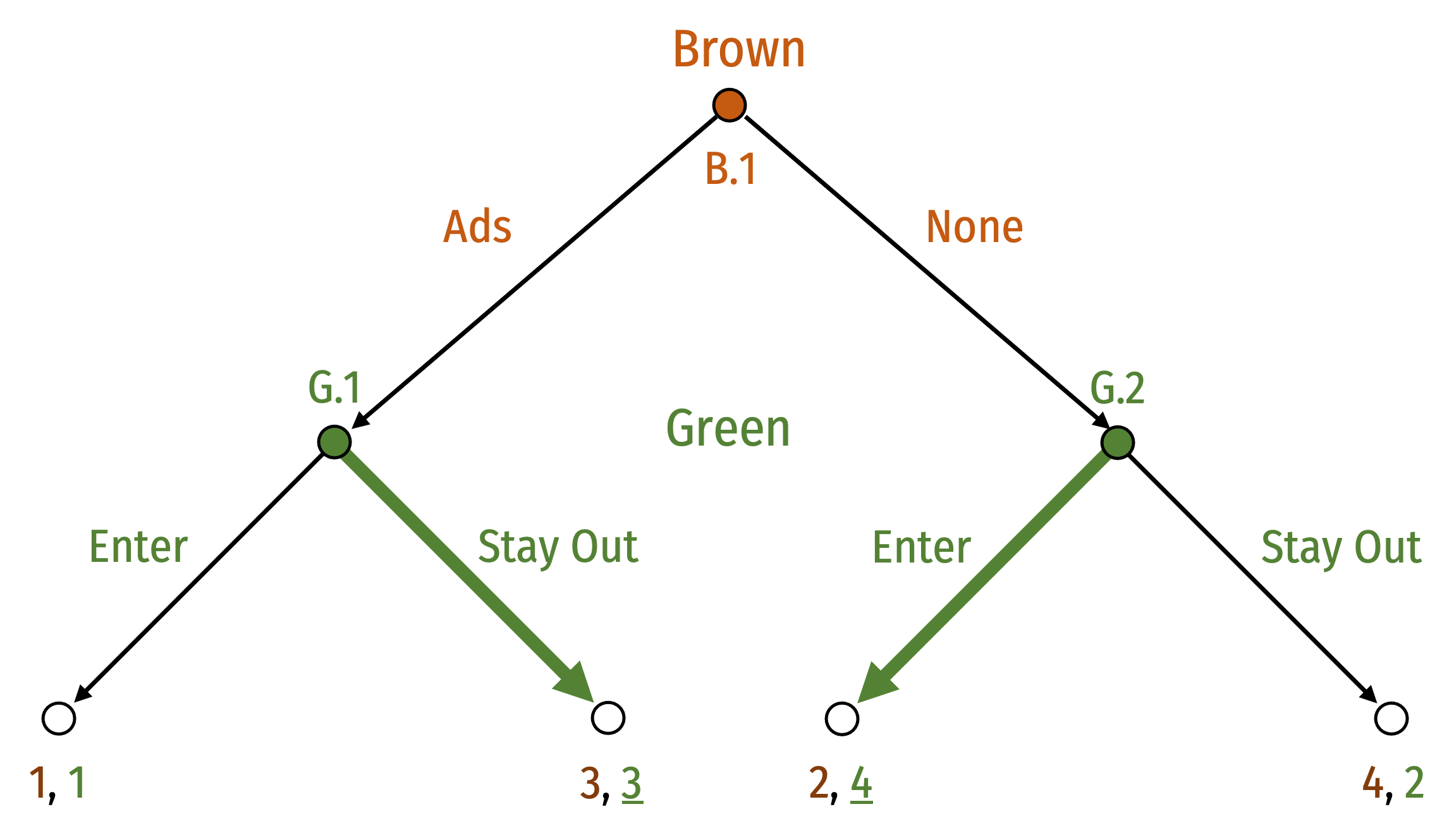
Senate Race Game: Solution

  • To apply backward induction, begin with the last-mover

  1. What will Green choose...

    • If Ads then Stay Out (at B.1)
    • If None then Enter (at B.2)

  2. Given this, what will Brown choose?

Senate Race Game: Solution

  • To apply backward induction, begin with the last-mover

  1. What will Green choose...

    • If Ads then Stay Out (at B.1)
    • If None then Enter (at B.2)

  2. Given this, what will Brown choose?

    • (Ads, Stay Out) ≻ (None, Enter)
    • (3) ≻ (2)

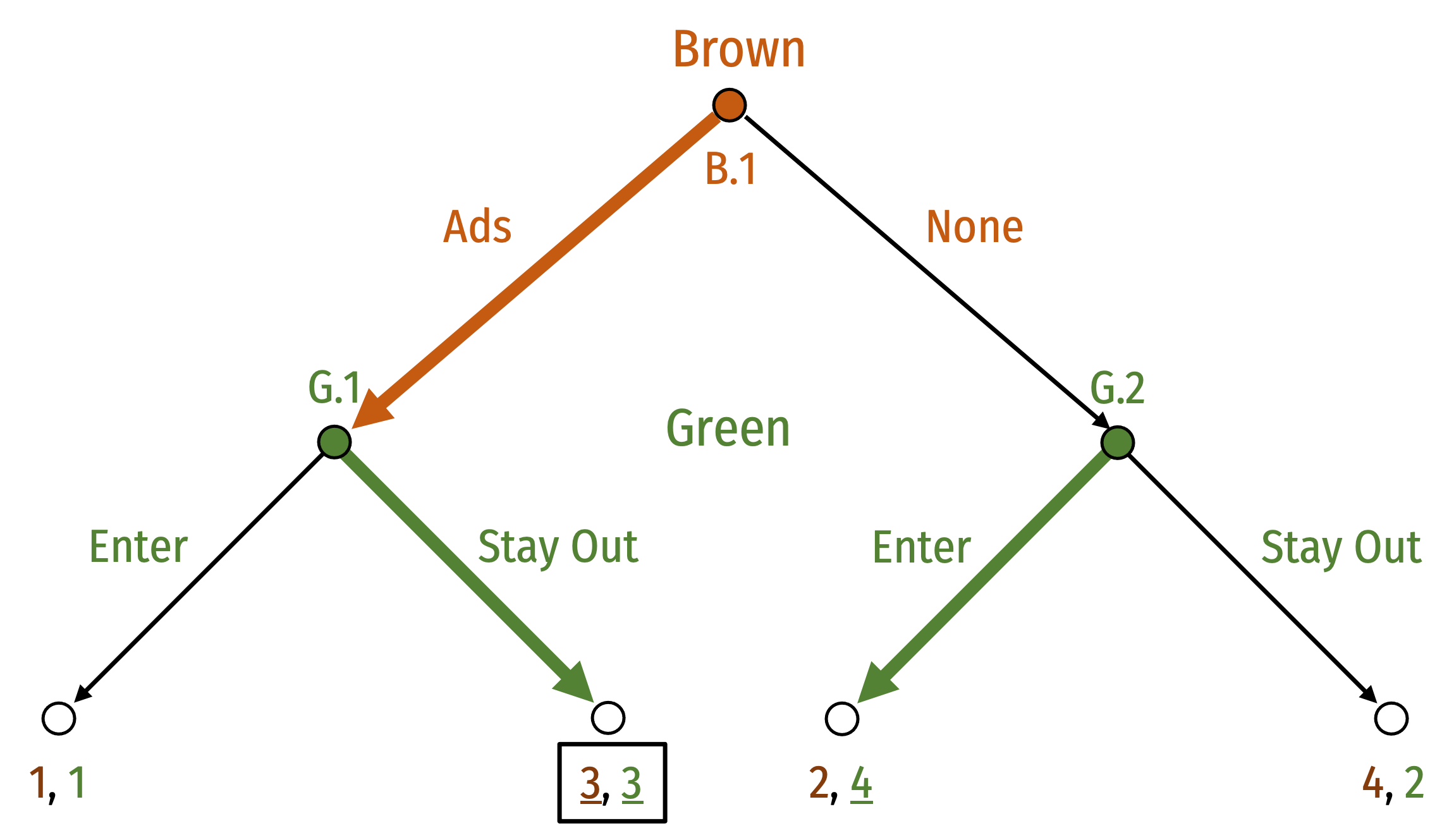
Senate Race Game: Solution

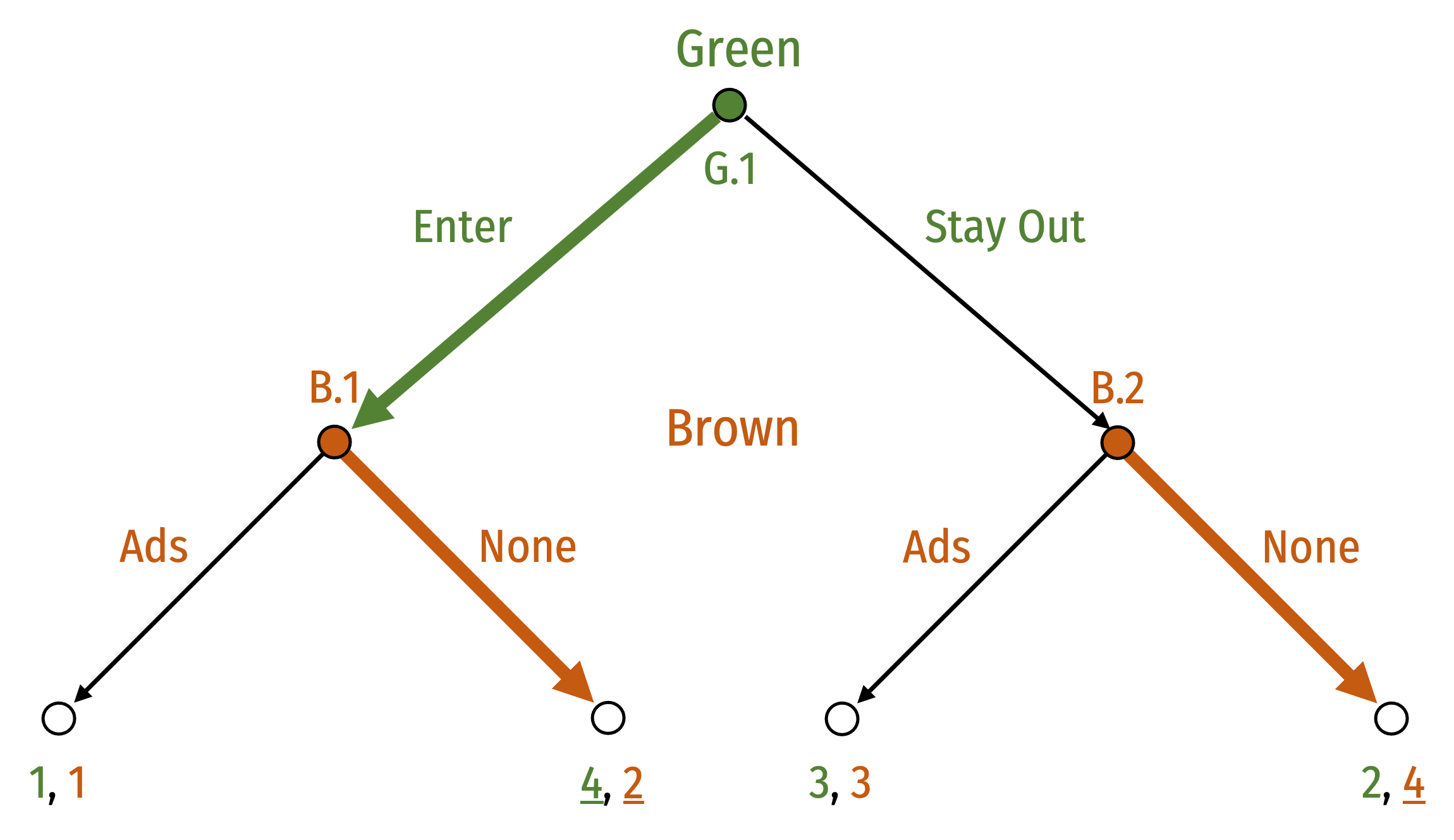
  • Equilibrium: (Ads, (Stay Out, Enter))

  • Notation:

    • Brown's strategy shows his decision at B.1 only
    • Green's strategy shows her decisions at (G.1,G.2)

Mover Advantages

Mover Advantage: Senate Race Game

  • Is there an order advantage to the Senate Race game?

  • We saw what happens when Brown moves first

  • Change the rules so that Green moves first and see what changes

    • Be careful how you write the payoffs!

Mover Advantage: Senate Race Game

  • Is there an order advantage to the Senate Race game?

  • We saw what happens when Brown moves first

  • Change the rules so that Green moves first and see what changes

    • Be careful how you write the payoffs!

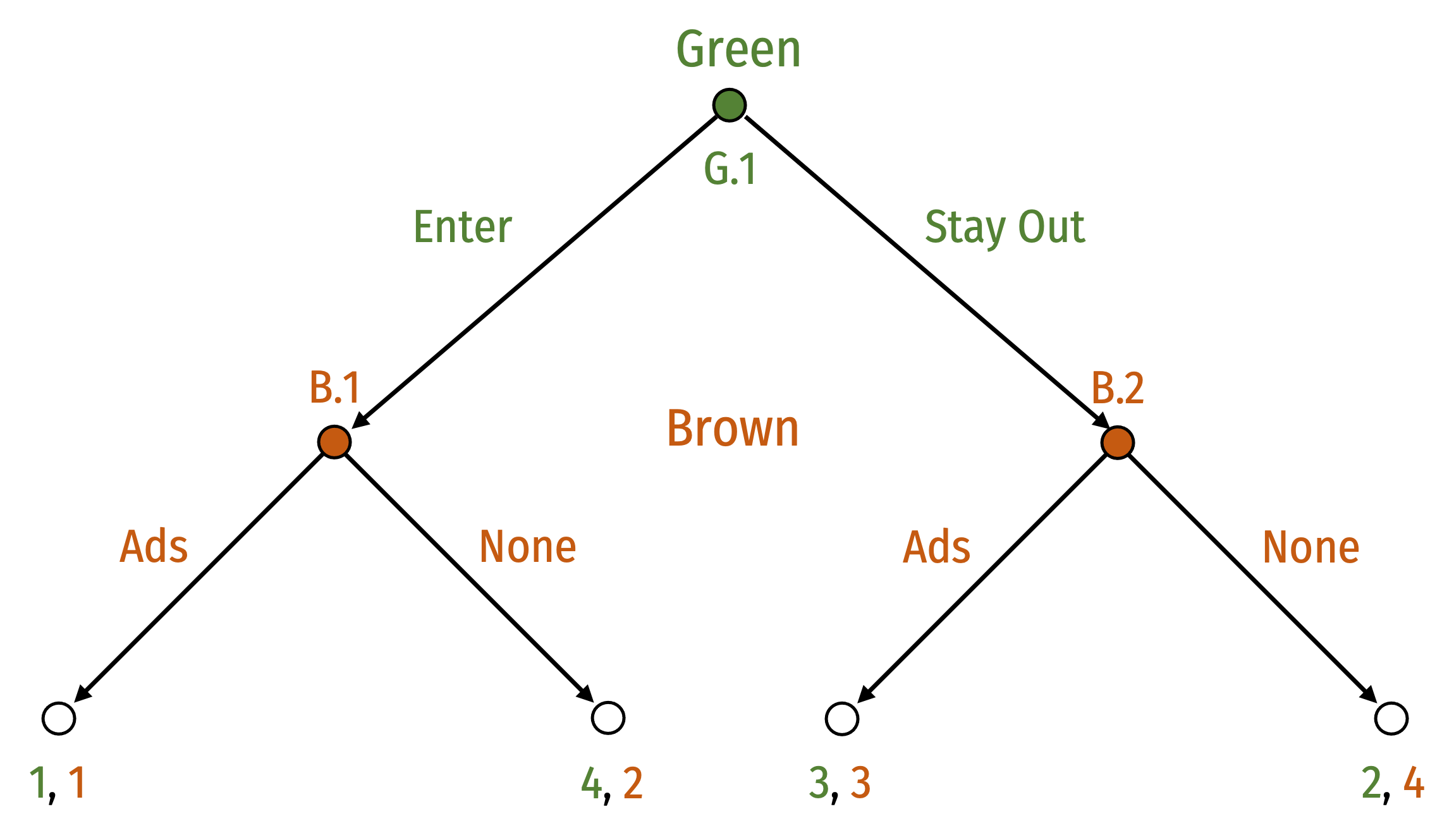
Mover Advantage: Senate Race Game

  • Green has 2 strategies:
    1. Enter at G.1
    2. Stay Out at G.1

Mover Advantage: Senate Race Game

  • Green has 2 strategies:

    1. Enter at G.1
    2. Stay Out at G.1

  • Brown has 4 strategies:

    1. Ads at B.1; Ads at B.2
    2. Ads at B.1; None at B.2
    3. None at B.1; Ads at B.2
    4. None at B.1; None at B.2

Mover Advantage: Senate Race Game

  • Apply backwards induction
  1. What will Brown choose
    • If Green were to Enter?
    • If Green were to Stay Out?

Mover Advantage: Senate Race Game

  • Apply backwards induction
  1. What will Brown choose
    • If Enter then None
    • If Stay Out then None
  • Note None becomes a dominant strategy for Brown!
  1. Given this, what will Green choose?

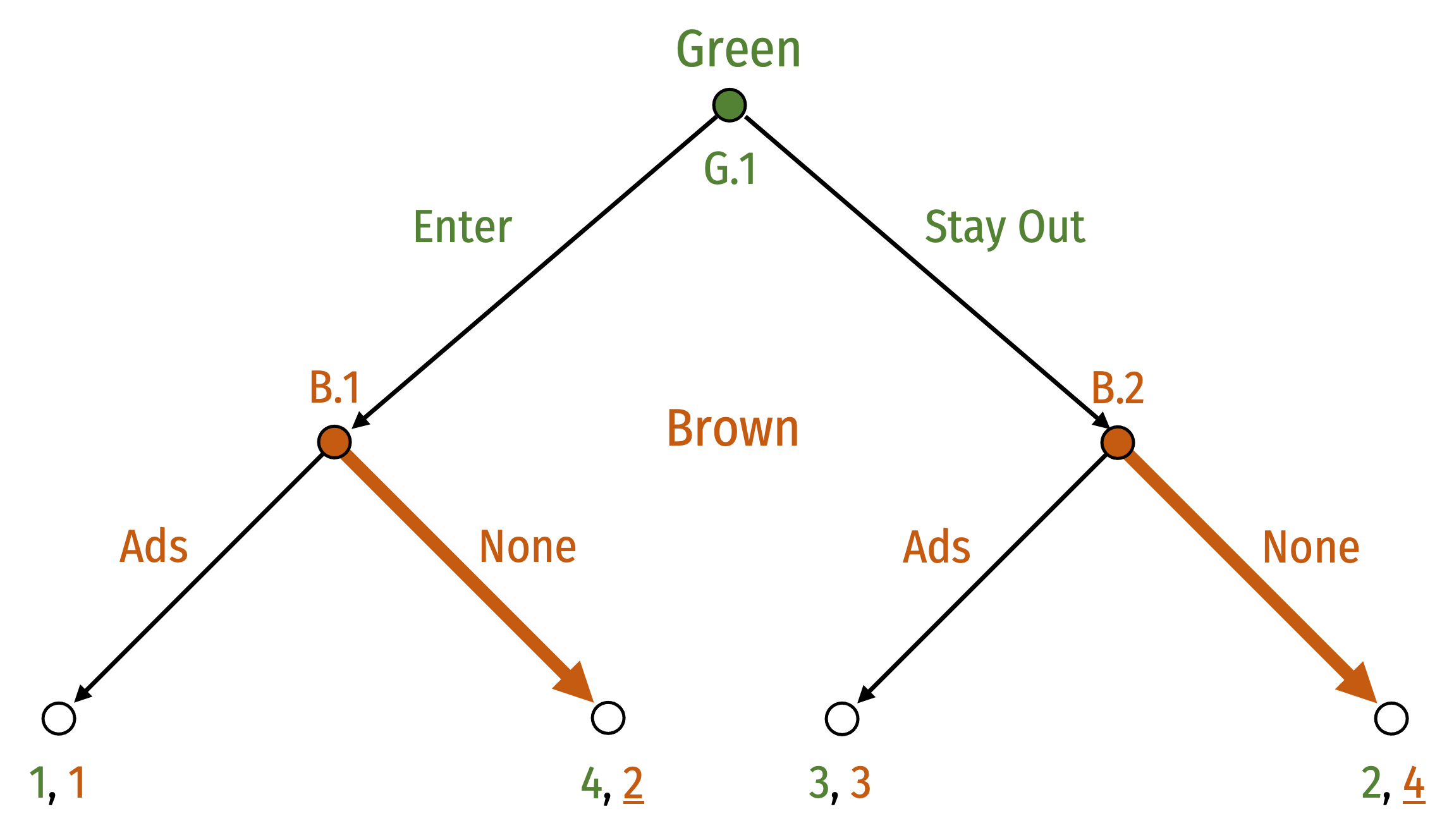
Mover Advantage: Senate Race Game

  • Equilibrium: (Enter, (None, None))

    • Payoffs of (4, 2)

  • Recall original outcome (Ads, (Stay Out, Enter))

    • Payoffs of (3, 3)

  • Brown is worse-off moving second vs. first; Green is better off moving first vs. second

    • A first-mover advantage for either player

When Order Matters

  • In general, to see if order matters, reverse sequence of moves and see if outcomes differ

  • Games with first-mover advantage:

    • Century Mark
    • Tic-tac-toe
    • Chess? Checkers?

  • Games with second-mover advantage:

    • Free riders
    • Business?

When Order Matters

Clayton Christensen

“When you look across the sweep of business history, most companies that once seemed successful—the best practitioners of best practice—were in the middle of the pack (or, worse, the back of it) a decade or two later...What often causes this lagging behind are two principles of good management taught in business schools: that you should always listen to and respond to the needs of your best customers, and that you should focus investments on those innovations that promise the highest returns. But these two principles, in practice, actually sow the seeds of every successful company's ultimate demise,” (ix-x).

Christensen, Clayton, 2016[1997], The Innovator's Dilemma: When New Technologies Cause Great Firms to Fail

When Order Matters

Peter Thiel

“You've probably heard about 'first mover advantage': if you're the first entrant into a market, you can capture significant market share while competitors scramble to get started. But moving first is a tactic, not a goal...[B]eing the first mover doesn't do you any good if someone comes along and unseats you. It's much better to be the last mover—that is, to make the last great development in a specific market and enjoy years or even decades of monopoly profits.,” (57-58).

Thiel, Peter, 2014, Zero to One: Notes on Startups or How to Build the Future

Adding Players

Adding Players

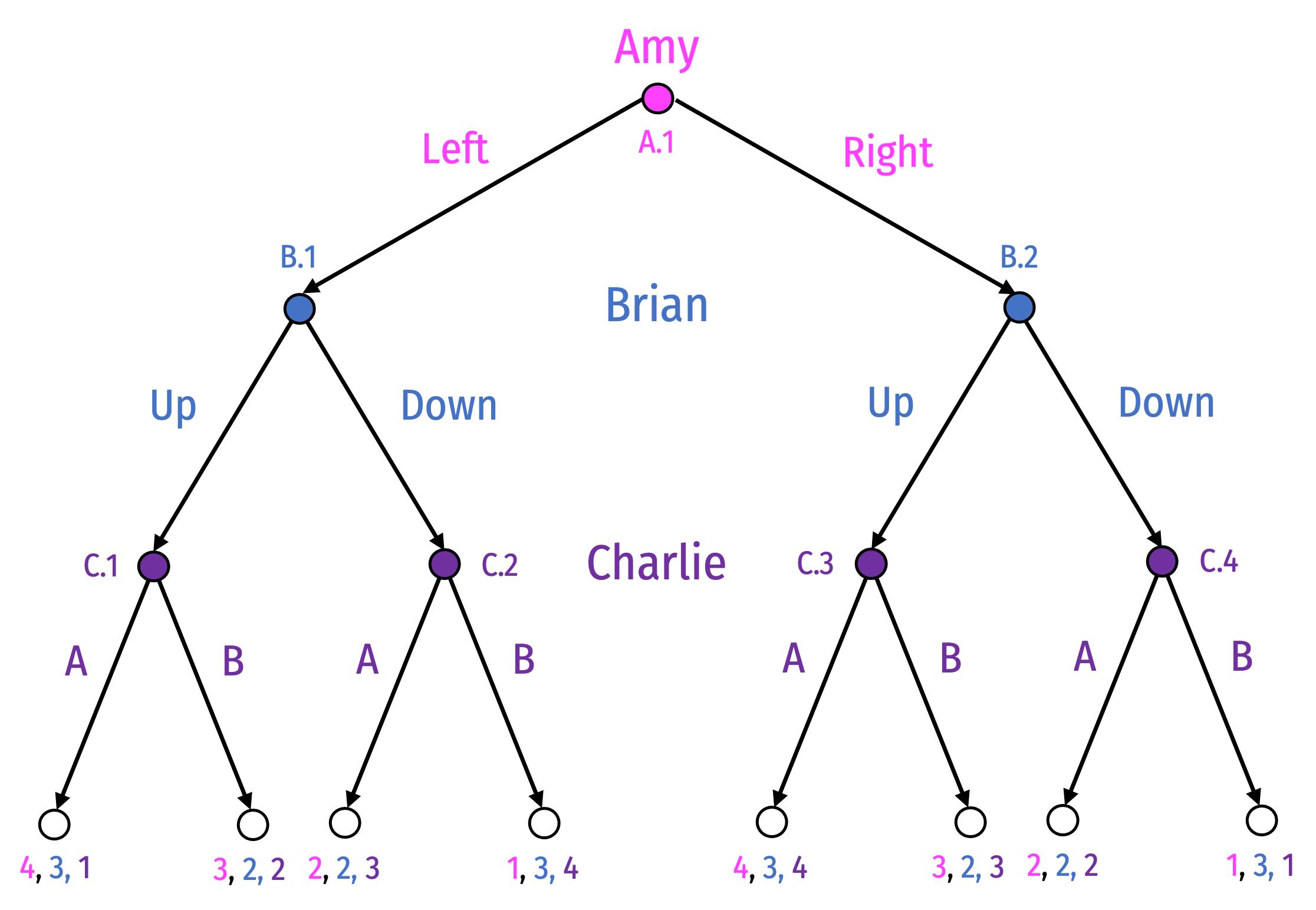
Adding Players

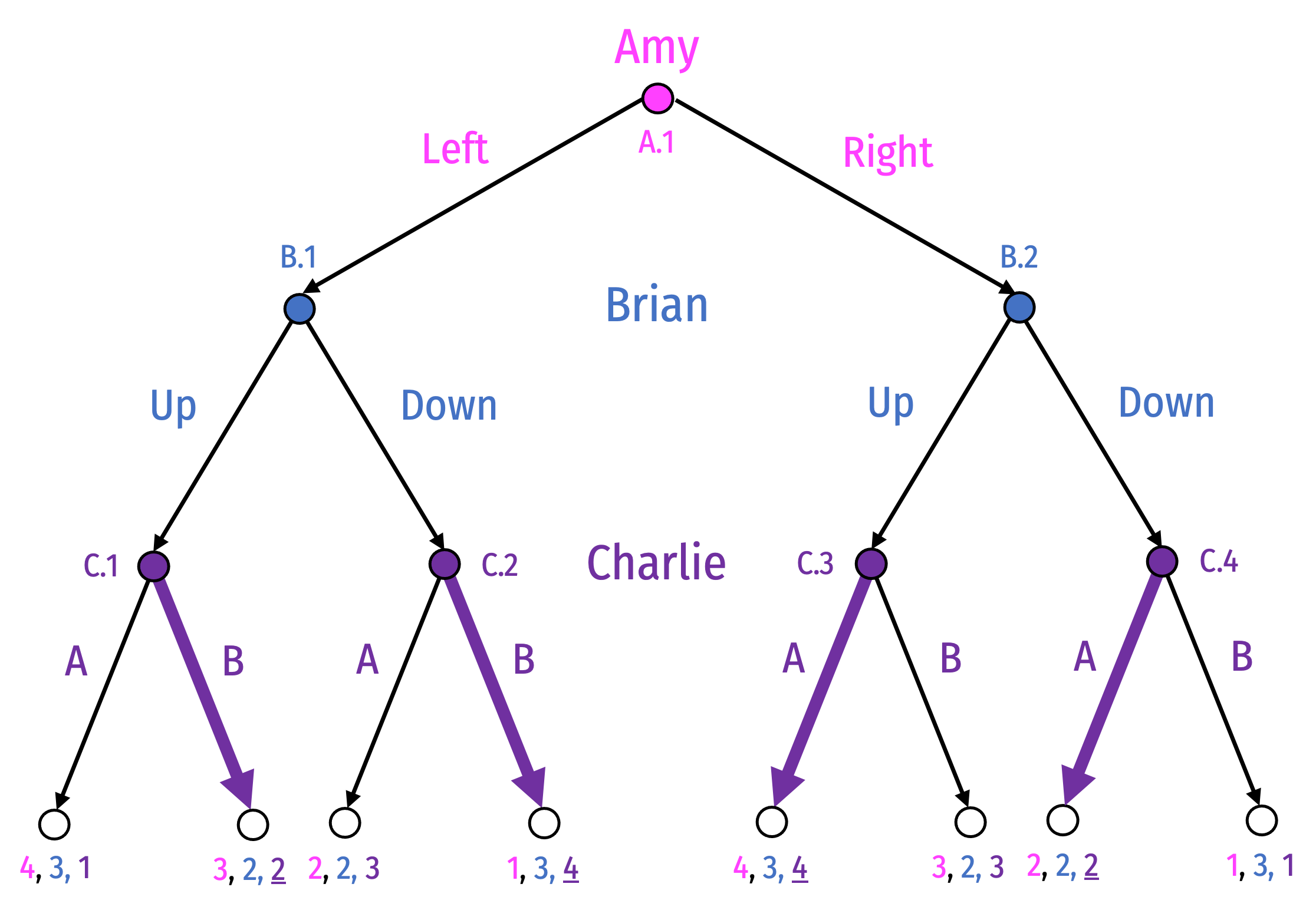
Adding Players

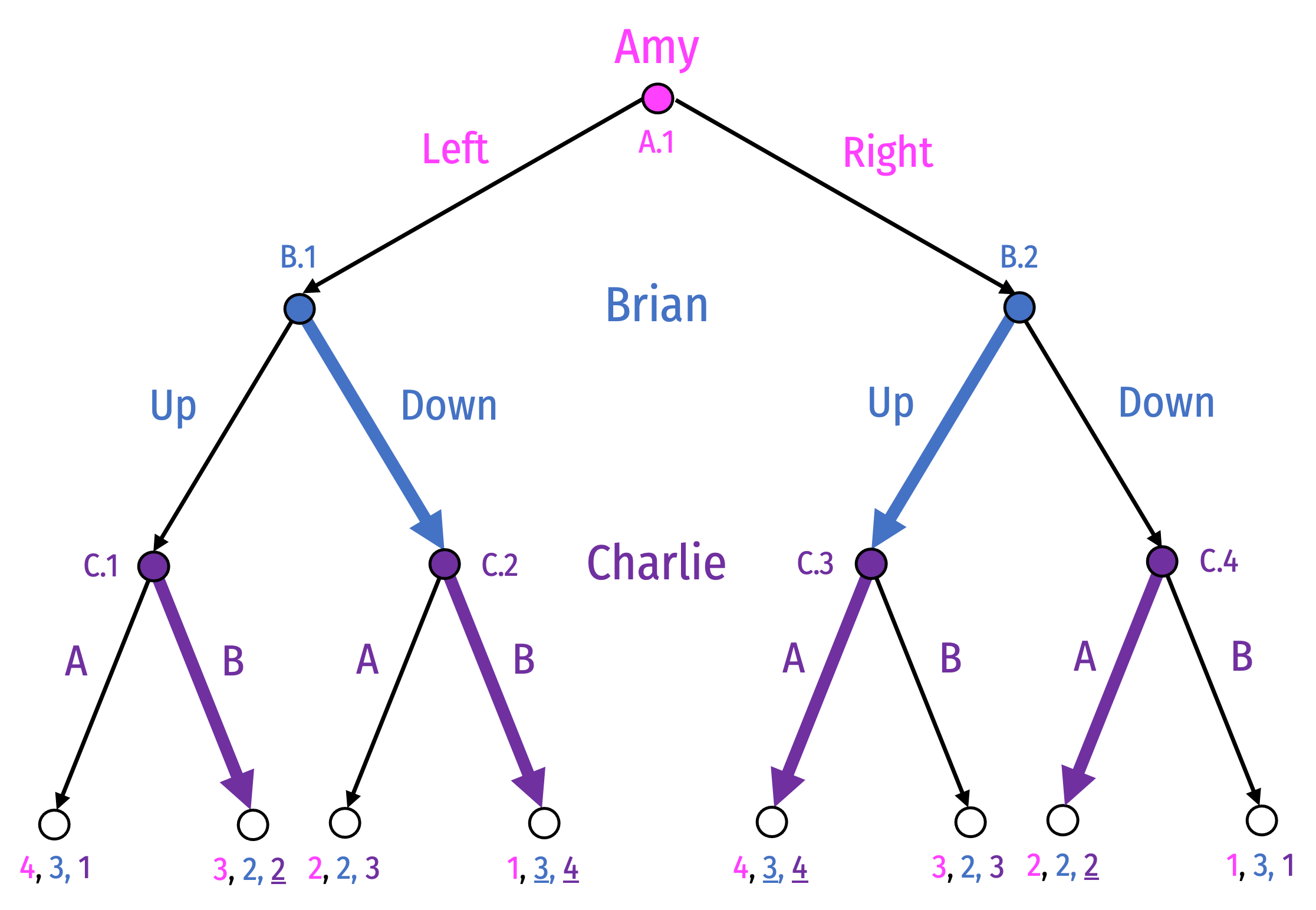
Adding Players

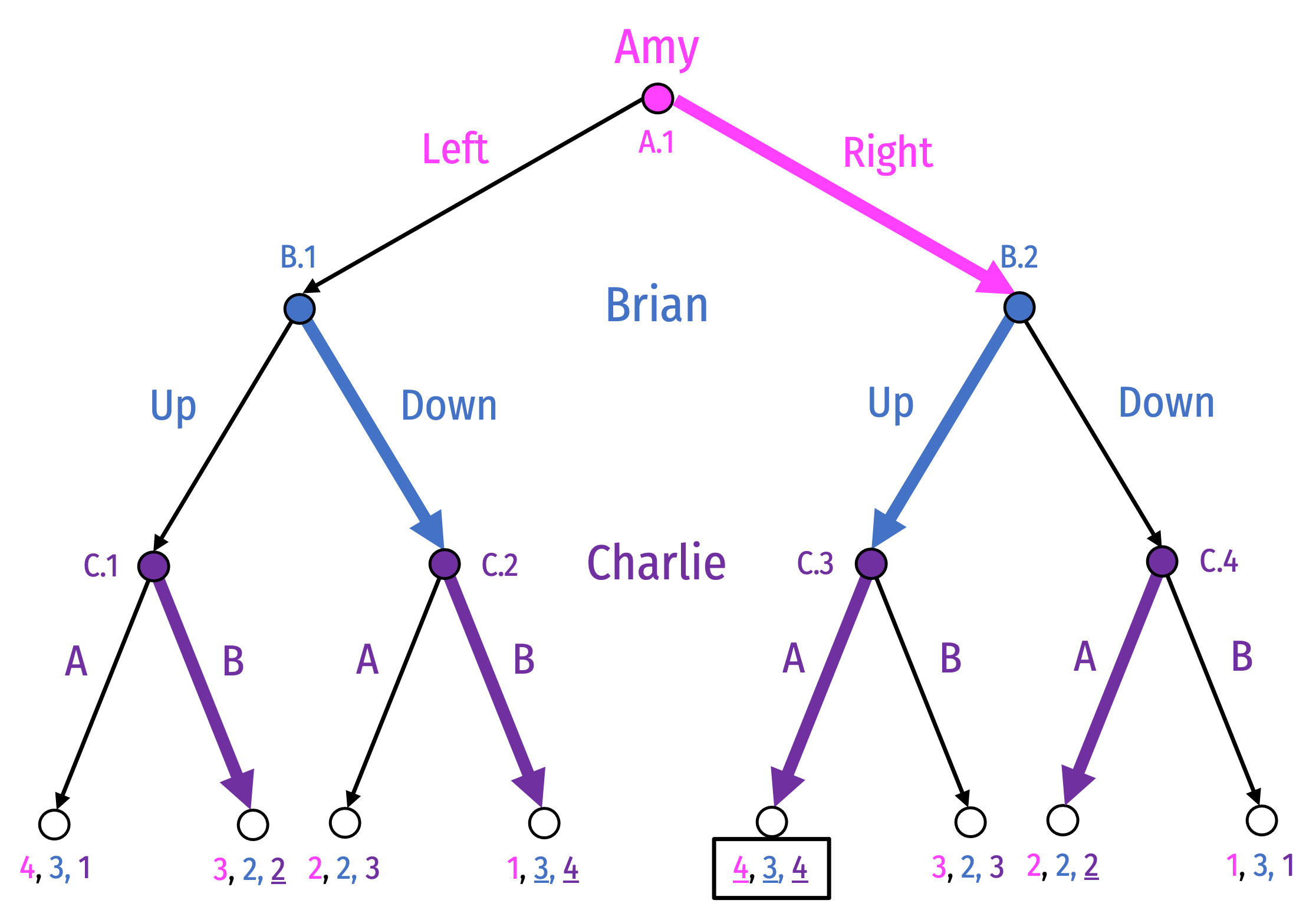
Adding Players

Equilibrium: {R, (D,U), (B,B,A,A) }

How About If We Change it to This

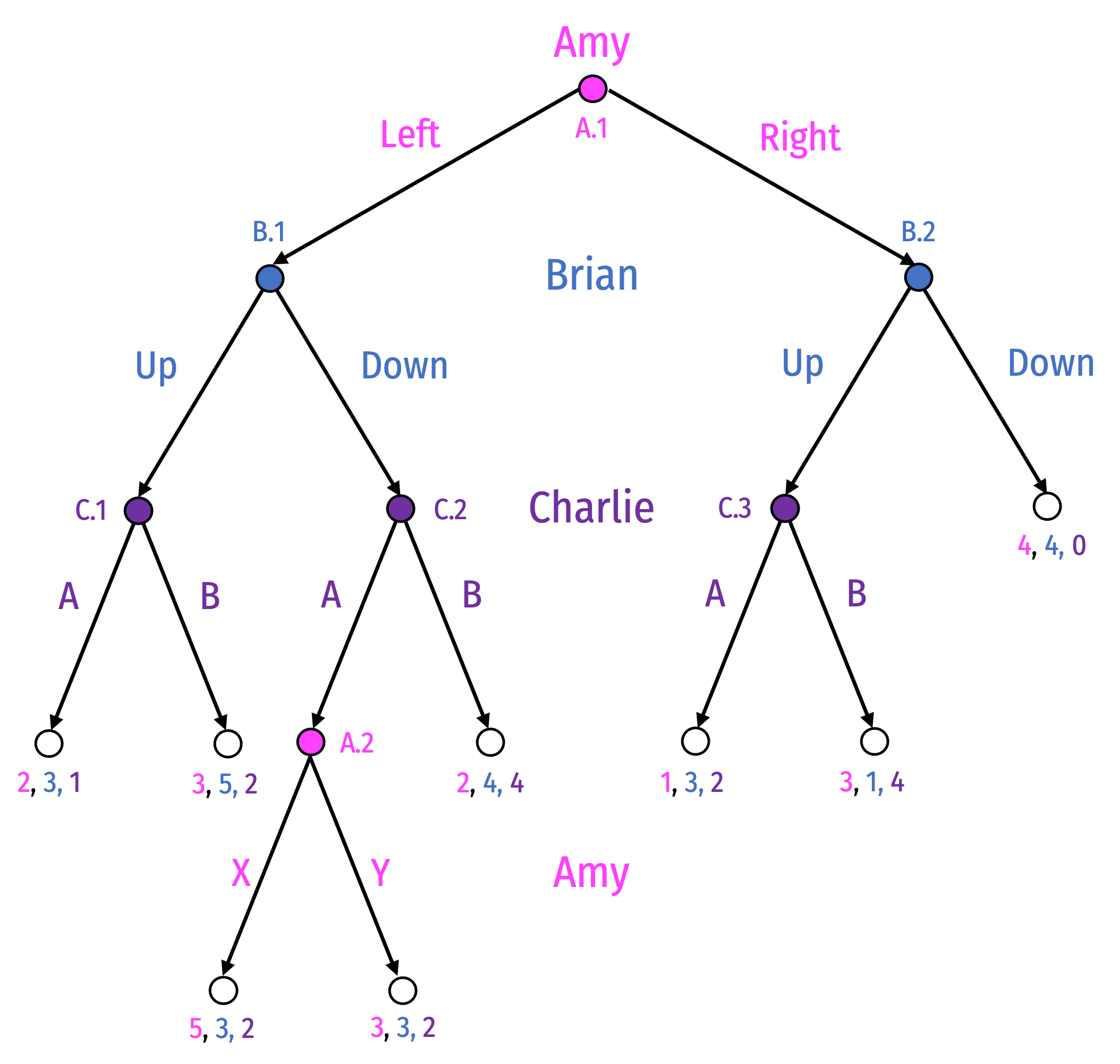
How About If We Change it to This

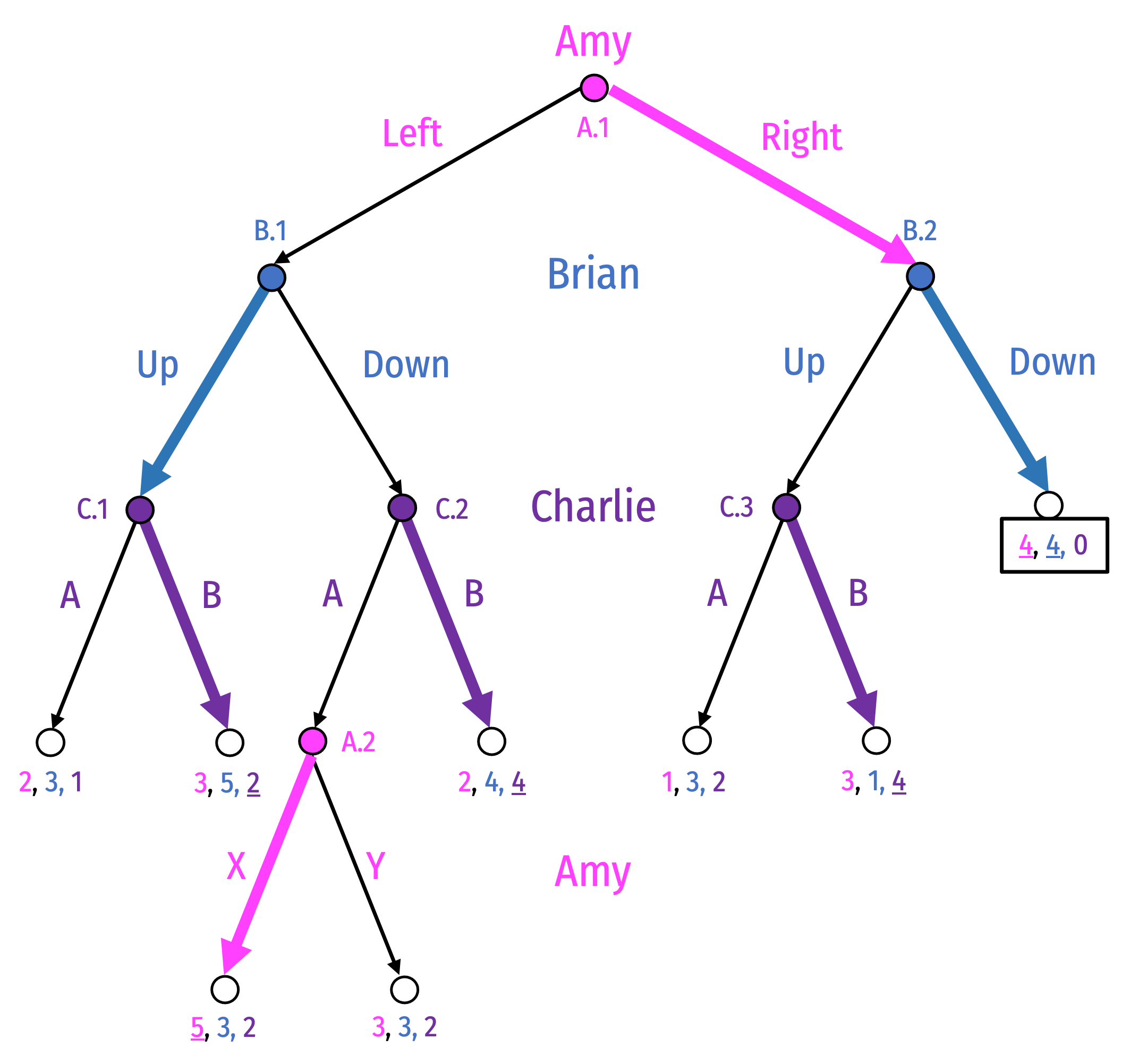
Equilibrium: {(R,X), (U,D), (B,B,B) }

Summary

  1. Construct a game tree
    • Place players in proper order
    • Specify which decisions are available to each player at each decision node
    • Specify payoffs to all players in terminal noides

Summary

  1. Construct a game tree

    • Place players in proper order
    • Specify which decisions are available to each player at each decision node
    • Specify payoffs to all players in terminal noides

  2. Solve for rollback equilibrium

    • Start with last-mover, identify best response, prune all other branches
    • Work successively backwards to the root
    • Highlight equilibrium path of play
    • Equilibrium = set of (complete!) strategies all players are playing

How Reasonable is Rollback Thinking?

How Reasonable is Rollback Thinking?

  • Useful for simple games with few players & moves

  • More difficult for complex games (more moves and/or players)

    • Tic-tac-toe has 9! or 362,880 possible moves

How Reasonable is Rollback Thinking?

  • Chess estimated to have 10120 possible moves

  • Players need rules to assign “payoffs” to non-terminal nodes, an “intermediate value function”

    • Humans < computers at anticipating future moves
    • Humans > computers at mid-game intuition and experience

Garry Kasparov vs. IBM's Deep Blue

How Reasonable is Rollback Thinking?

How Reasonable is Rollback Thinking?

How Richard Hatch won the first Survivor

How Reasonable is Rollback Thinking?

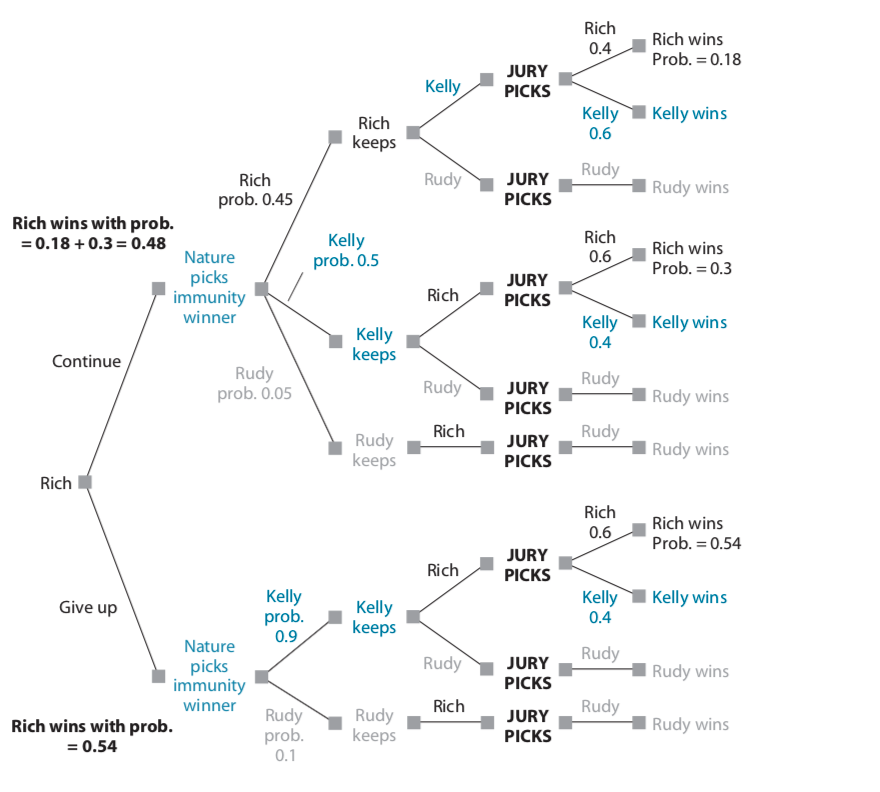
Games on Moblab

Split the Pie

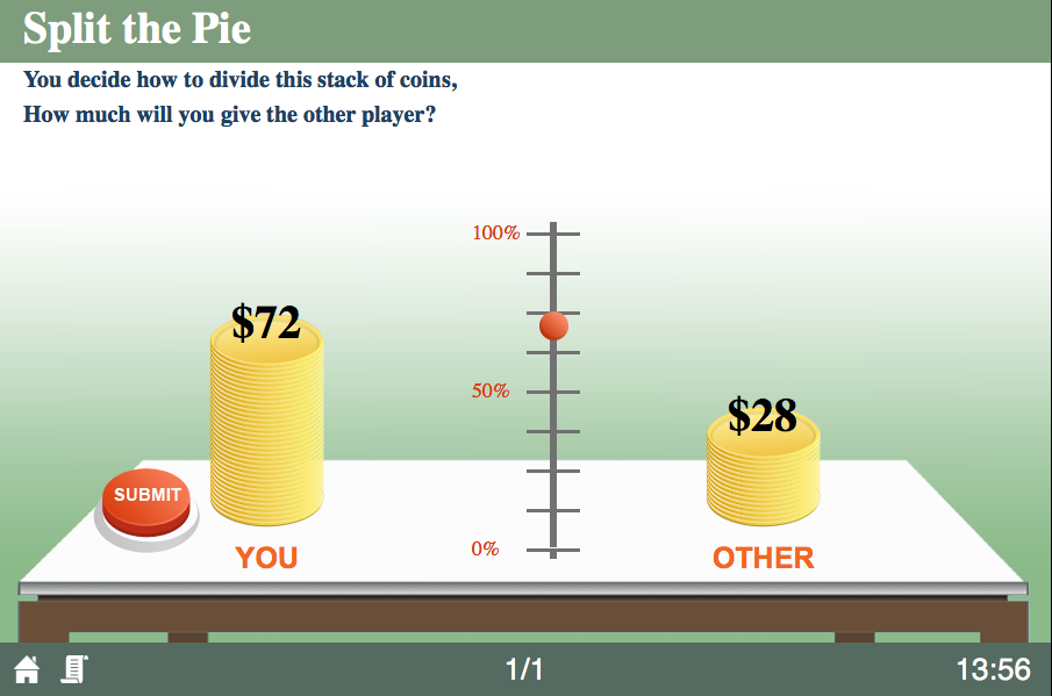
The Dictator Game

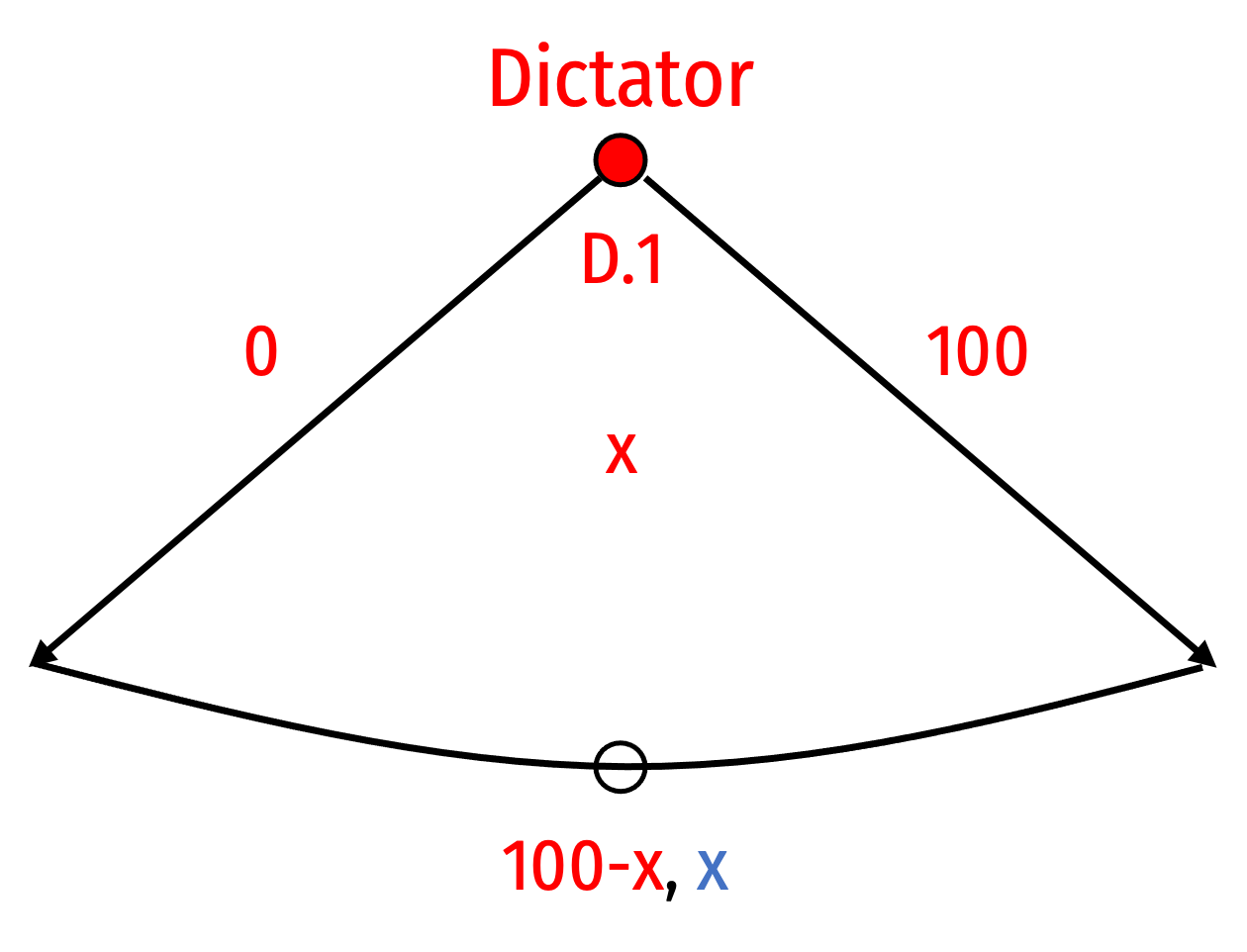
  • Famously called “The Dictator Game”

    • Player 1 is given money (e.g. $100) and decides how much of that (x) to give to Player 2

  • Used in experiments to measure altruism in societies

  • What’s the rollback equilibrium?

  • What do we see in the real world?

Split the Pie, Modified

Split the Pie, Modified

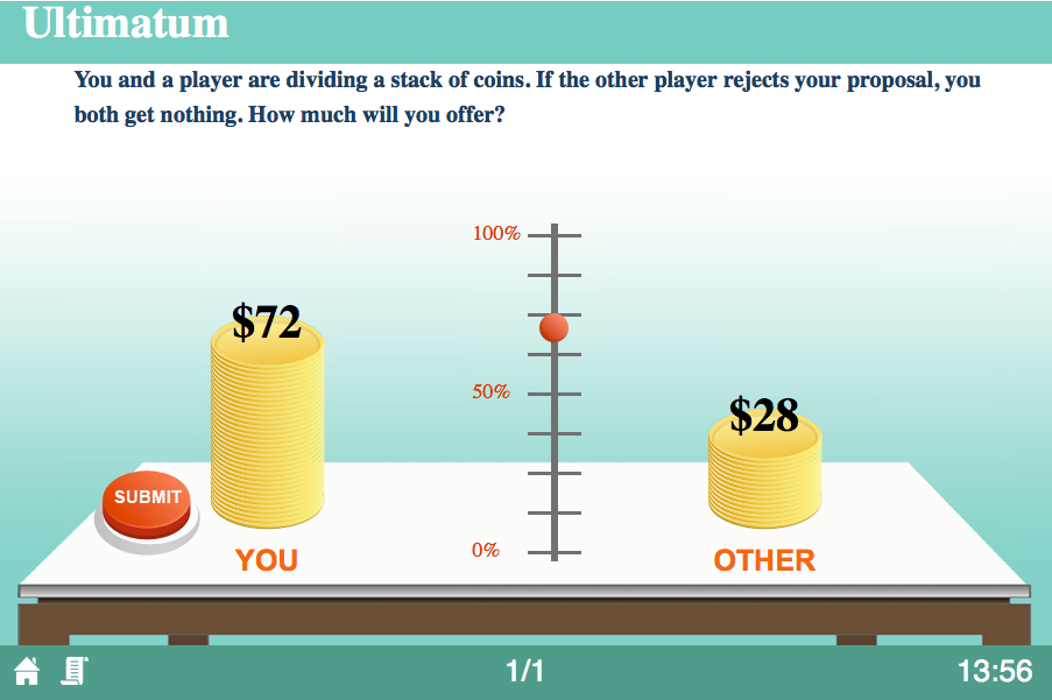
Ultimatum Game

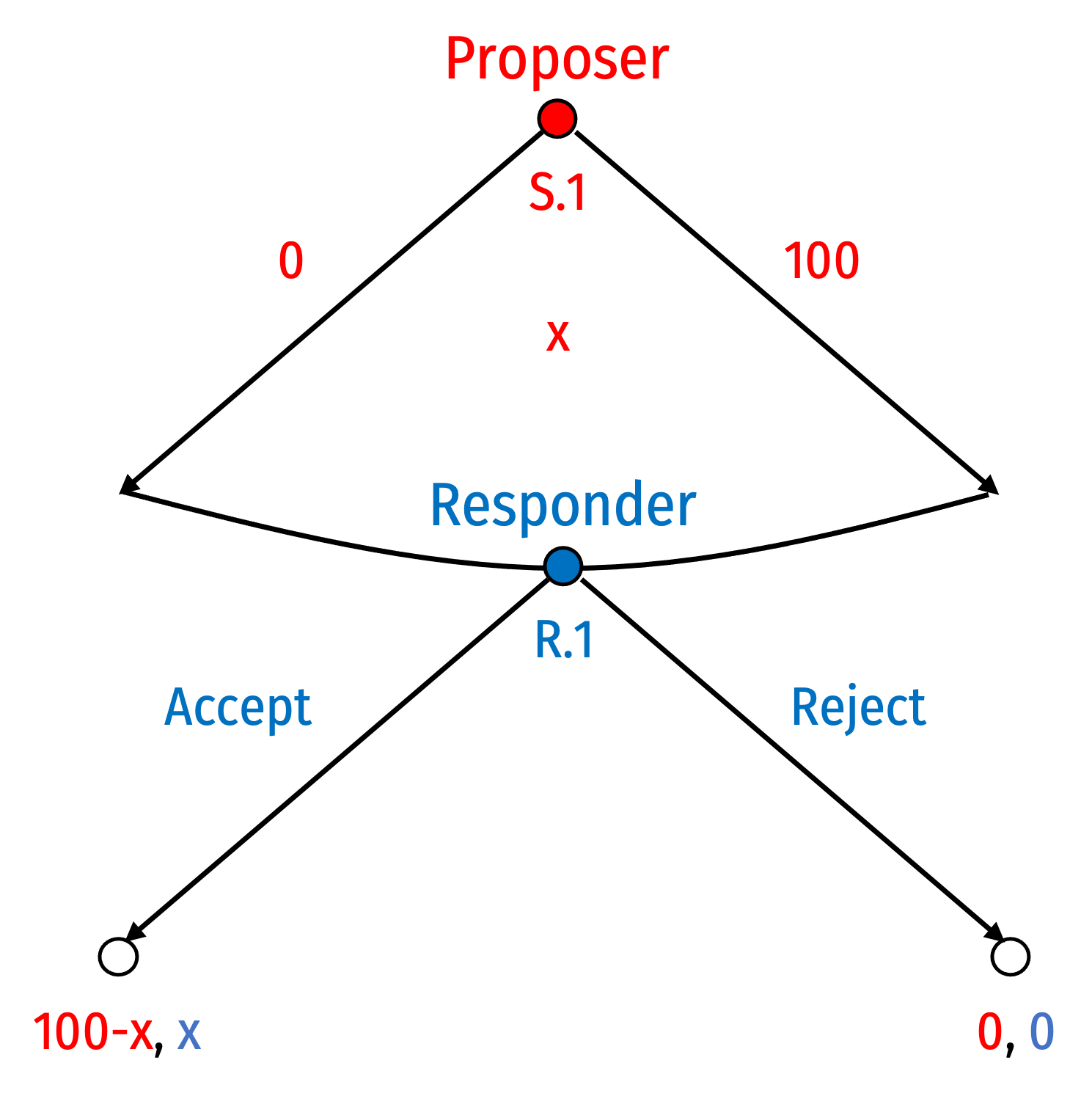
  • Equally famous game used in experiments, the Ultimatum game

    • After Player 1 decides how much (x) to give to Player 2, Player 2 can Accept or Reject (where nobody gets anything)

  • What’s the rollback equilibrium?

  • What do we see in the real world?

Pass the Pumpkin

Pass the Pumpkin

Centipede Game

  • Called the Centipede game

    • Players take turns deciding between taking money out of a pot vs. passing; after each pass, the money in the pot grows, until a set final turn

  • What's the rollback equilibrium?

  • What do we see in the real world?

Centipede Game

Outline

Games in Extensive Form

Mover Advantages

How Reasonable is Rollback Thinking?

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
oTile View: Overview of Slides
Esc Back to slideshow