+ - 0:00:00
Notes for current slide
Notes for next slide

1.4 — Simultaneous Games & Normal Form

ECON 316 • Game Theory • Fall 2021

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/gameF21
gameF21.classes.ryansafner.com

Outline

Games in Normal Form

Dominance-Solvability

Best-Response

Depicting Three Player Games

Simultaneous Games

Simultaneous Games

  • Players must make choices simultaneously, but under strategic uncertainty

    • Don't know which strategies other players are playing before you choose yours

  • Possible strategic choices and payoffs of each outcome to each player are known by all players

  • Must think not only about own best strategic choice, but also the best strategic choice of other player(s)

Flat Tire Story

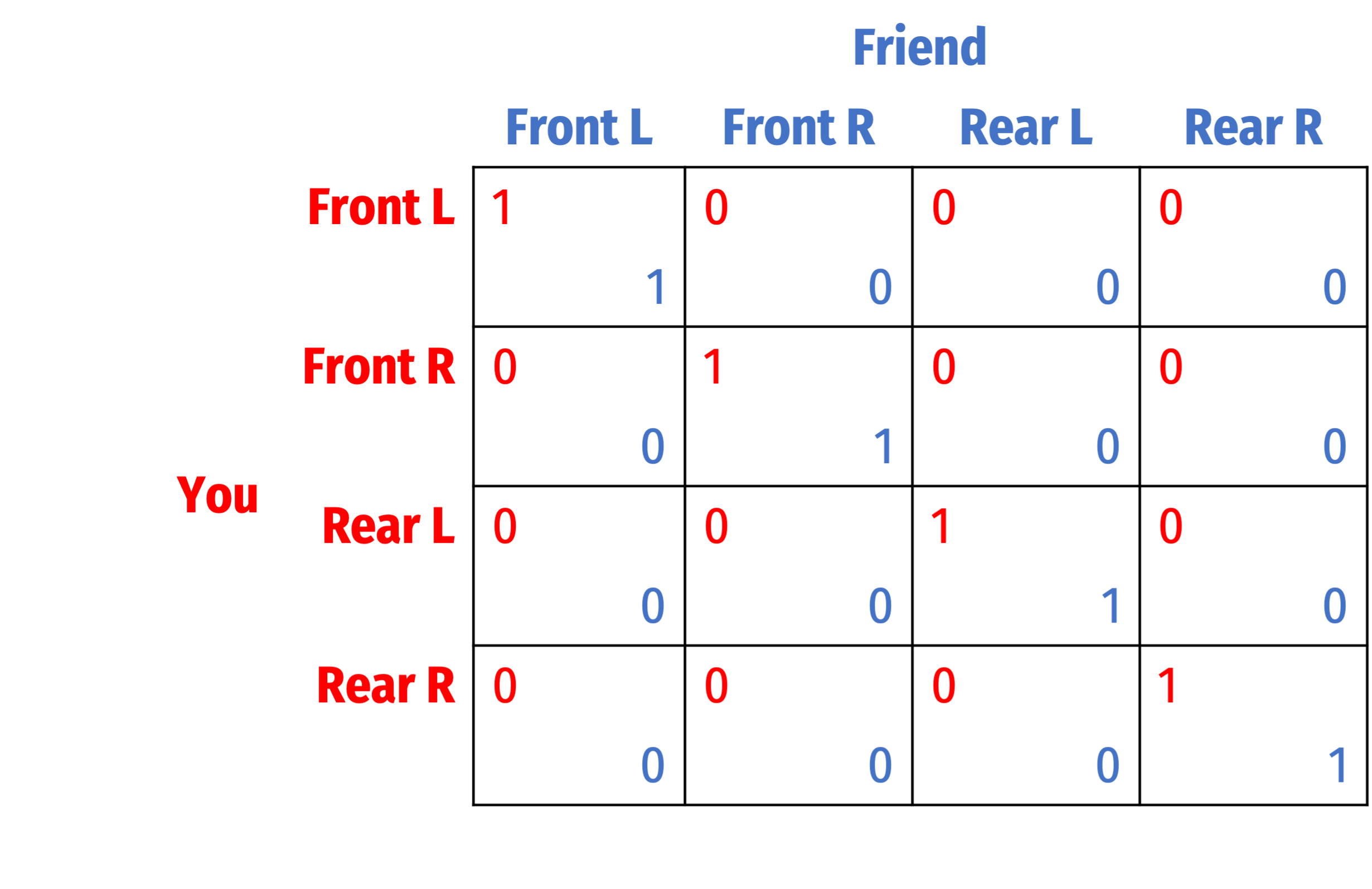
Games in Normal Form

  • Normal or strategic form

  • By convention Row Player is Player 1, Column player is Player 2

    • First payoff in a cell goes to Row, second to Column
    • But order doesn’t matter (!)

  • Dimensions of matrix

    • Rows: possible strategies available to Row
    • Columns: possible strategies available to Column

  • For now, we only look at discrete strategies (and a single decision per player)

Nash Equilibrium, Again

  • Again, in a Nash equilibrium, no player wants to change strategies given the strategies played by all other players

    • Equivalently, each player is playing a best response to other players' strategies

  • Today we will learn several methods to search for Nash equilibria in simultaneous games

Cell-by-Cell Inspection

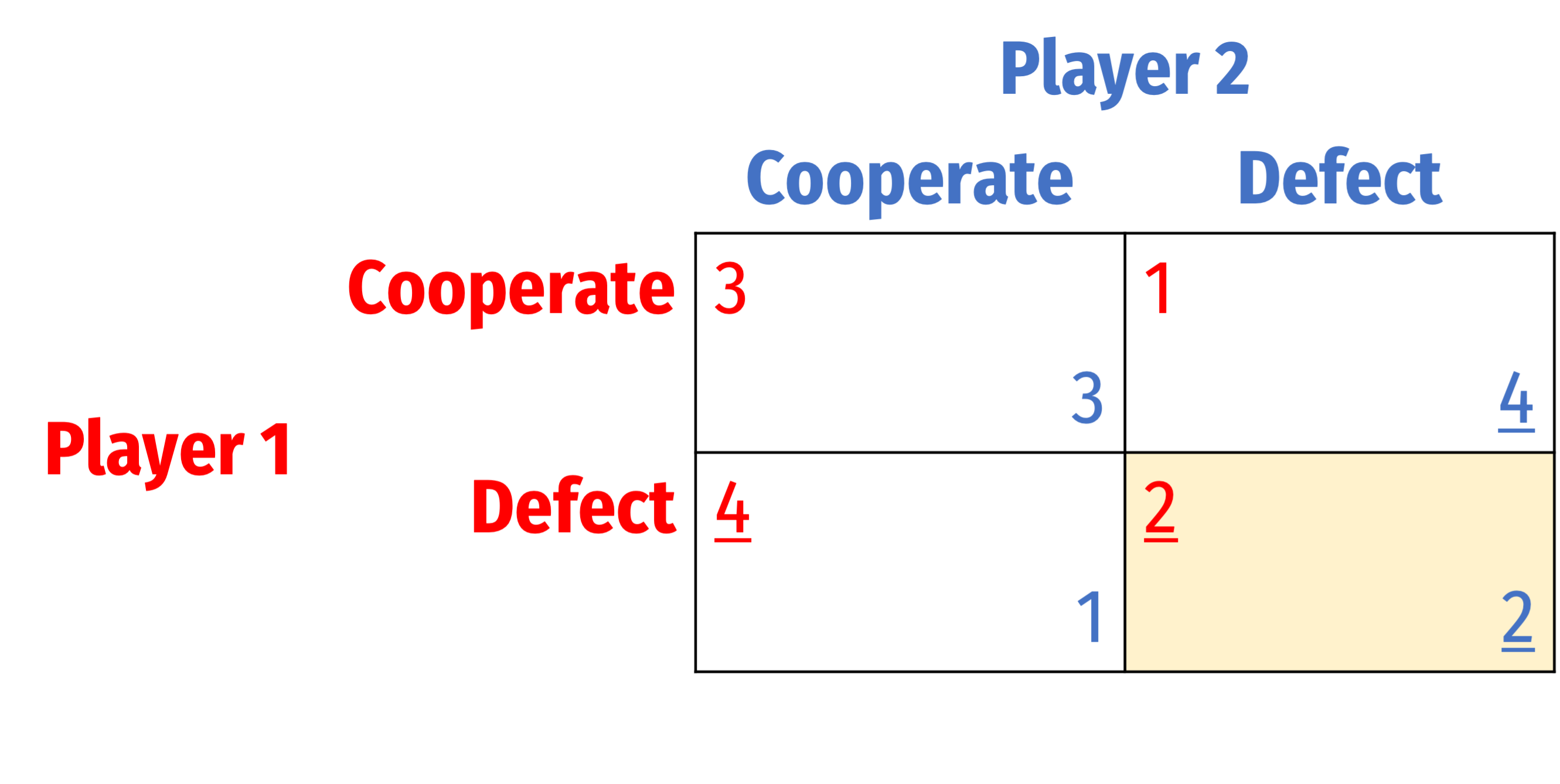
  • Consider again the prisoners' dilemma

  • Consider each outcome and ask, does any player want to change strategies, given what the other player is doing?

    1. (C, C)
    2. (C, D)
    3. (D, C)
    4. (D, D)

Cell-by-Cell Inspection

  • Consider again the prisoners' dilemma

  • Consider each outcome and ask, does any player want to change strategies, given what the other player is doing?

    1. (C, C) ✅
    2. (C, D) ✅
    3. (D, C) ✅
    4. (D, D) ❌

  • If no player wants to switch strategies (given the others’), that outcome is a Nash equilibrium: (D, D)

Dominance Solvability

Dominance Solvability

  • One efficient (but not foolproof) method for finding solution: search for dominated strategies and eliminate them
    • like pruning branches of a sequential game tree

Dominance Solvability

  • A player has a dominant strategy when it yields a higher payoff than all other strategies available, regardless of what strategy the other player is playing
  • A player has a dominated strategy when it yields a lower payoff than all other strategies available, regardless of what strategy the other player is playing

Dominance Solvability

  • Consider the prisoners' dilemma

Dominance Solvability

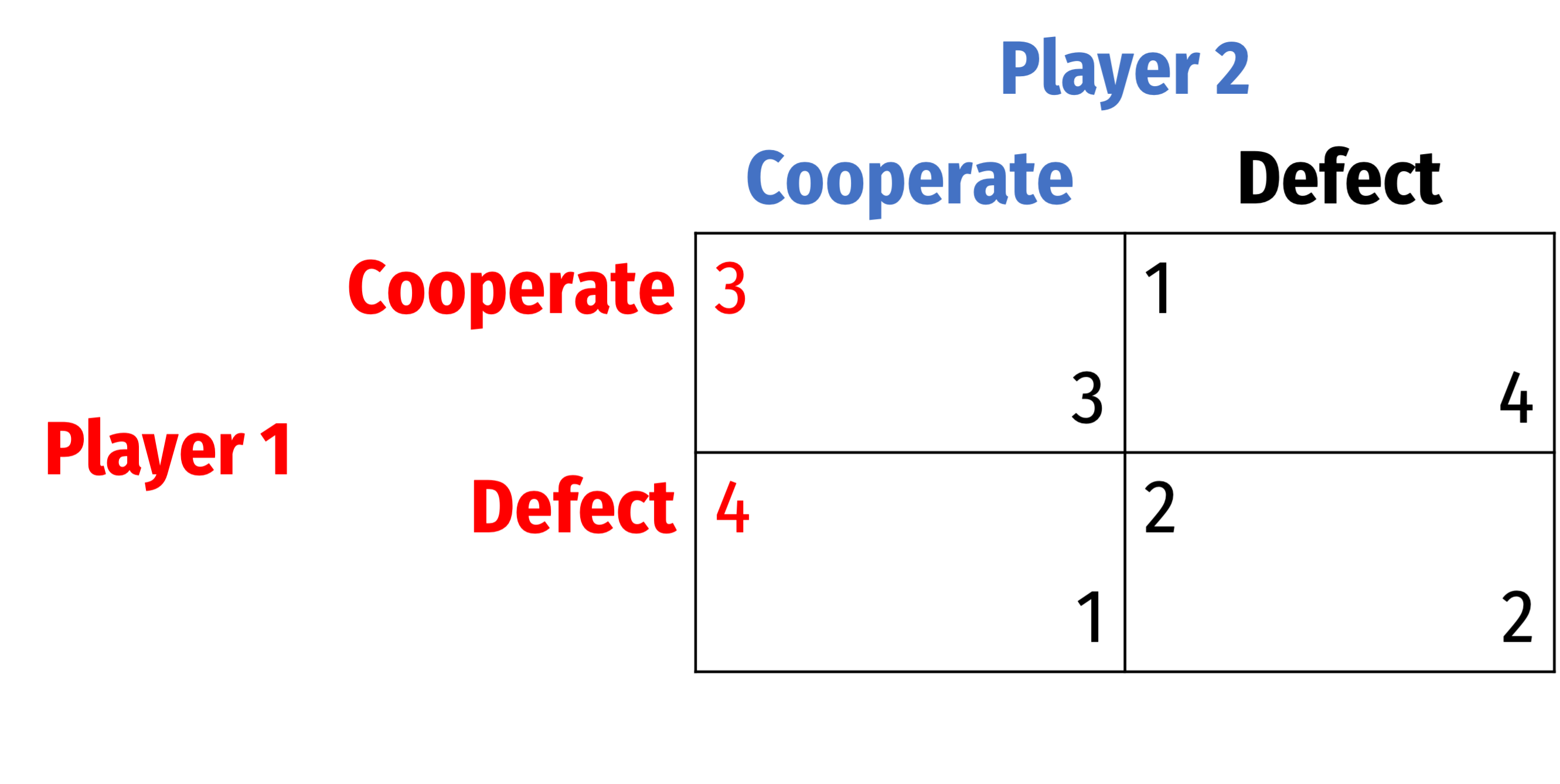
  • Consider the prisoners' dilemma

  • For Player 1...

Dominance Solvability

  • Consider the prisoners' dilemma

  • For Player 1...

Dominance Solvability

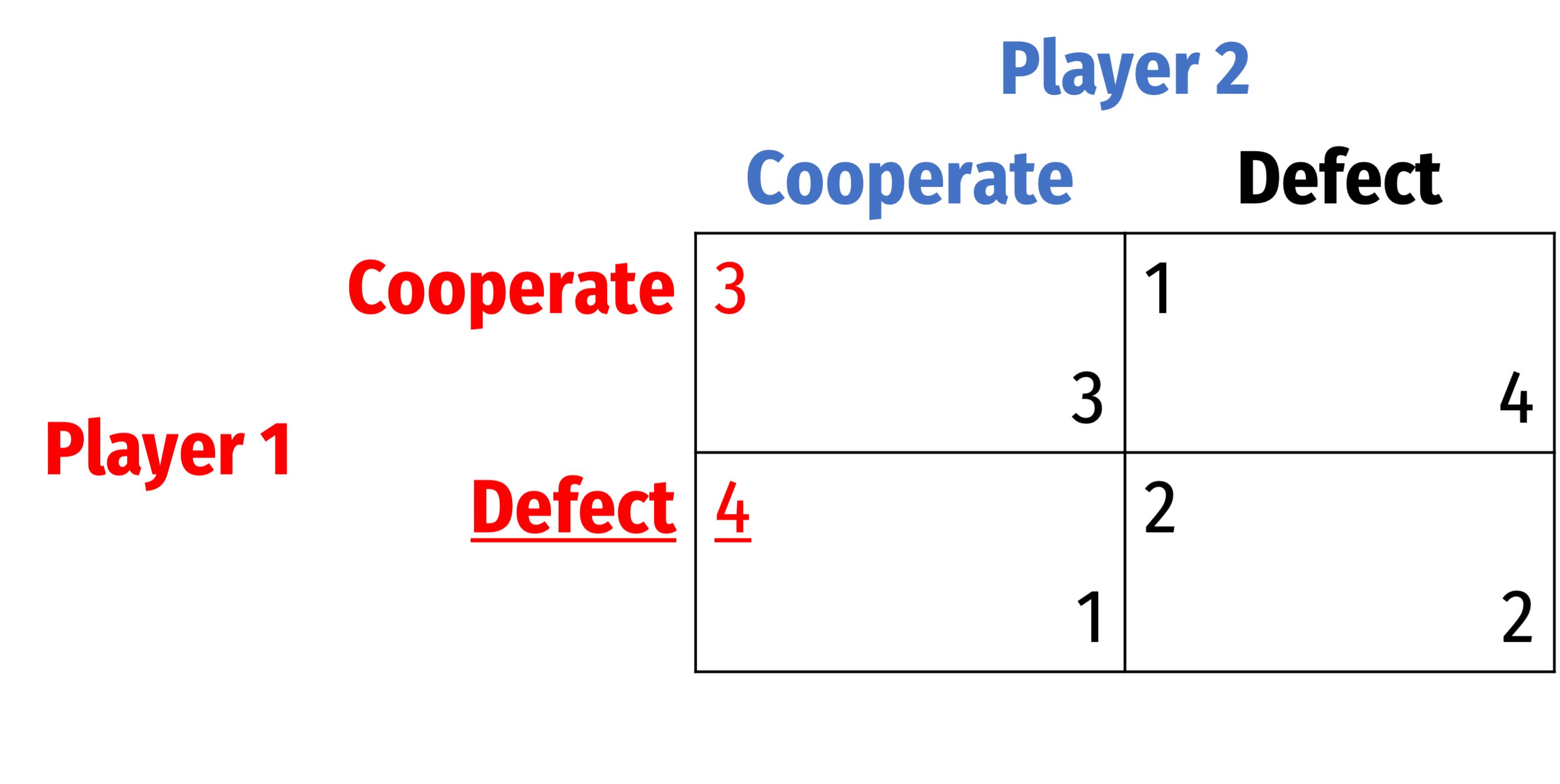
  • Consider the prisoners' dilemma

  • For Player 1...

Dominance Solvability

  • Consider the prisoners' dilemma

  • For Player 1...

Dominance Solvability

  • Consider the prisoners' dilemma

  • For Player 1: Cooperate is dominated by Defect

    • u1(D,C)≻u1(C,C)
    • u1(D,D)≻u1(C,D)

Dominance Solvability

  • Consider the prisoners' dilemma

  • For Player 1: Cooperate is dominated by Defect

    • u1(D,C)≻u1(C,C)
    • u1(D,D)≻u1(C,D)

  • Knowing Player 1 will never play Cooperate, we can delete that entire row from the game

Dominance Solvability

  • Consider the prisoners' dilemma

  • For Player 1: Cooperate is dominated by Defect

    • u1(D,C)≻u1(C,C)
    • u1(D,D)≻u1(C,D)

  • Knowing Player 1 will never play Cooperate, we can delete that entire row from the game

    • Player 2’s best response to Defect is to Defect

Dominance Solvability

  • Alternatively, we could consider Player 2

Dominance Solvability

  • Alternatively, we could consider Player 2

  • For Player 2...

Dominance Solvability

  • Alternatively, we could consider Player 2

  • For Player 2...

Dominance Solvability

  • Alternatively, we could consider Player 2

  • For Player 2...

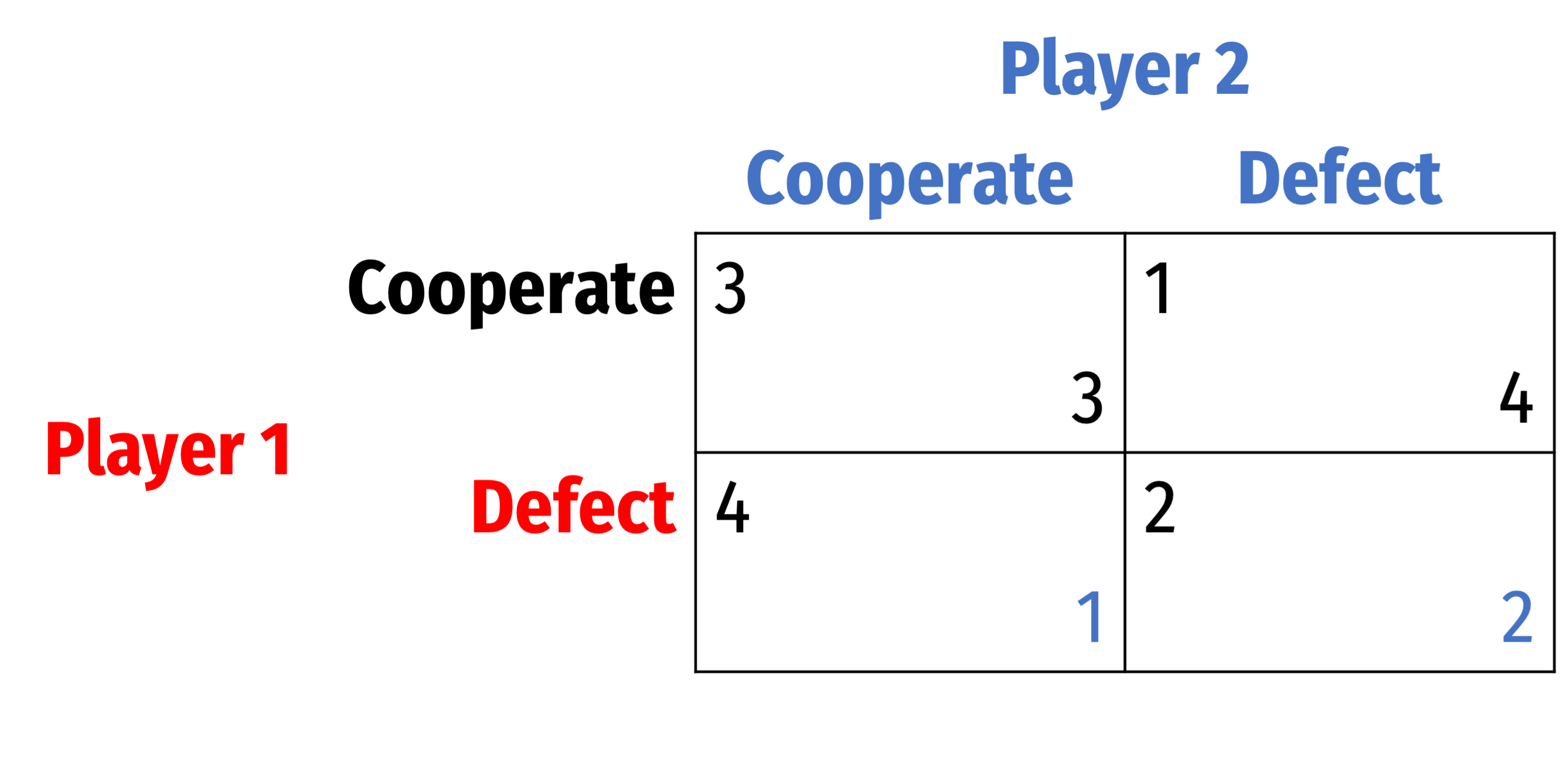
Dominance Solvability

  • Alternatively, we could consider Player 2

  • For Player 2...

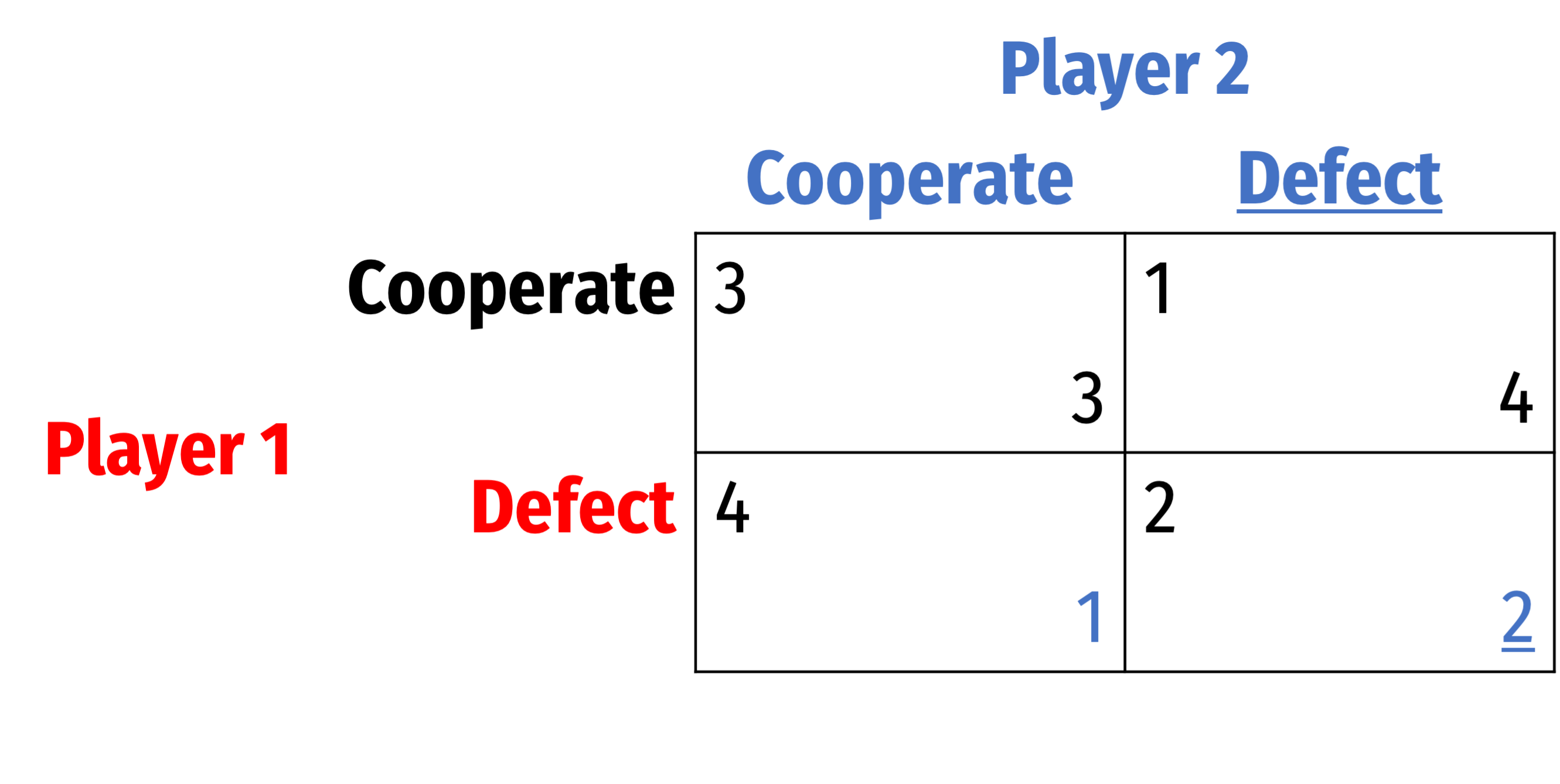
Dominance Solvability

  • Alternatively, we could consider Player 2

  • For Player 2: Cooperate is dominated by Defect

    • u2(C,D)≻u2(C,C)
    • u2(D,D)≻u2(D,C)

Dominance Solvability

  • Alternatively, we could consider Player 2

  • For Player 2: Cooperate is dominated by Defect

    • u2(C,D)≻u2(C,C)
    • u2(D,D)≻u2(D,C)

  • Knowing Player 2 will never play Cooperate, we can delete that entire column from the game

Dominance Solvability

  • Alternatively, we could consider Player 2

  • For Player 2: Cooperate is dominated by Defect

    • u2(C,D)≻u2(C,C)
    • u2(D,D)≻u2(D,C)

  • Knowing Player 2 will never play Cooperate, we can delete that entire column from the game

    • Player 1’s best response to Defect is to Defect

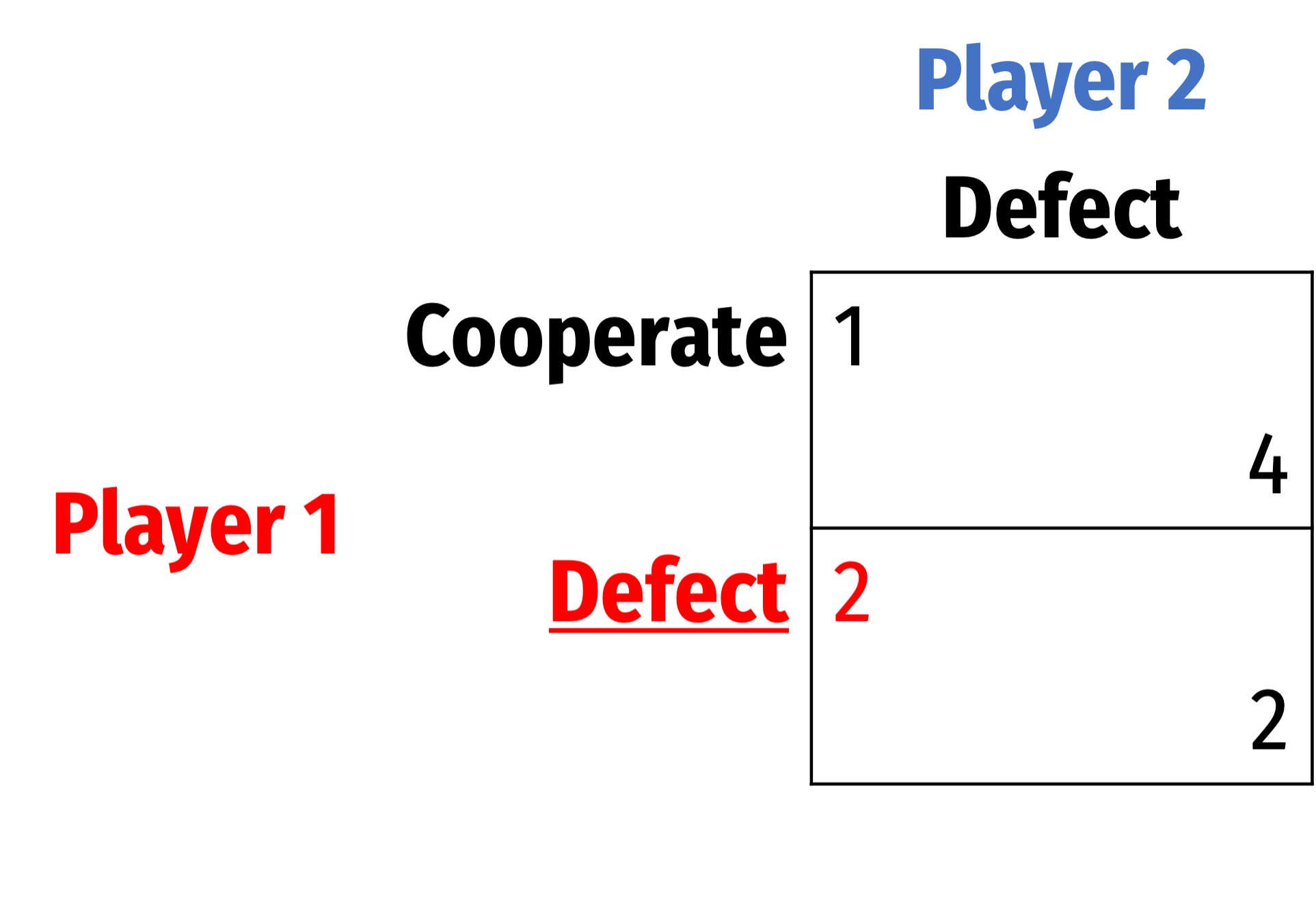
Dominance Solvability

  • Take the prisoners’ dilemma

  • Nash Equilibrium: (Defect, Defect)

    • neither player has an incentive to change strategy, given the other's strategy

  • Why can’t they both cooperate?

    • A clear Pareto improvement!

Pareto Efficiency and Games

  • Main feature of prisoners’ dilemma: the Nash equilibrium is Pareto inferior to another outcome (Cooperate, Cooperate)!

    • But that outcome is not a Nash equilibrium!
    • Dominant strategies to Defect

  • How can we ever get rational cooperation?

When One Player Has a Dominant Strategy

  • Congress determines fiscal policy

  • Can tax & spend to Balance Budget

  • Can tax & spend to run a Budget Deficit

  • Constant political pressure to spend more & tax less

    • May raise possibility of inflation

When One Player Has a Dominant Strategy

  • Federal Reserve determines monetary policy

  • Can target Low Interest Rates

  • Can target High Interest Rates

  • Generally wants to avoid inflation

    • Likes keeping interest rates low to stimulate Demand (if no threat of inflation)

When One Player Has a Dominant Strategy

  • Both players choose policy simultaneously and independently of each other

  • How to find the equilibrium of this game?

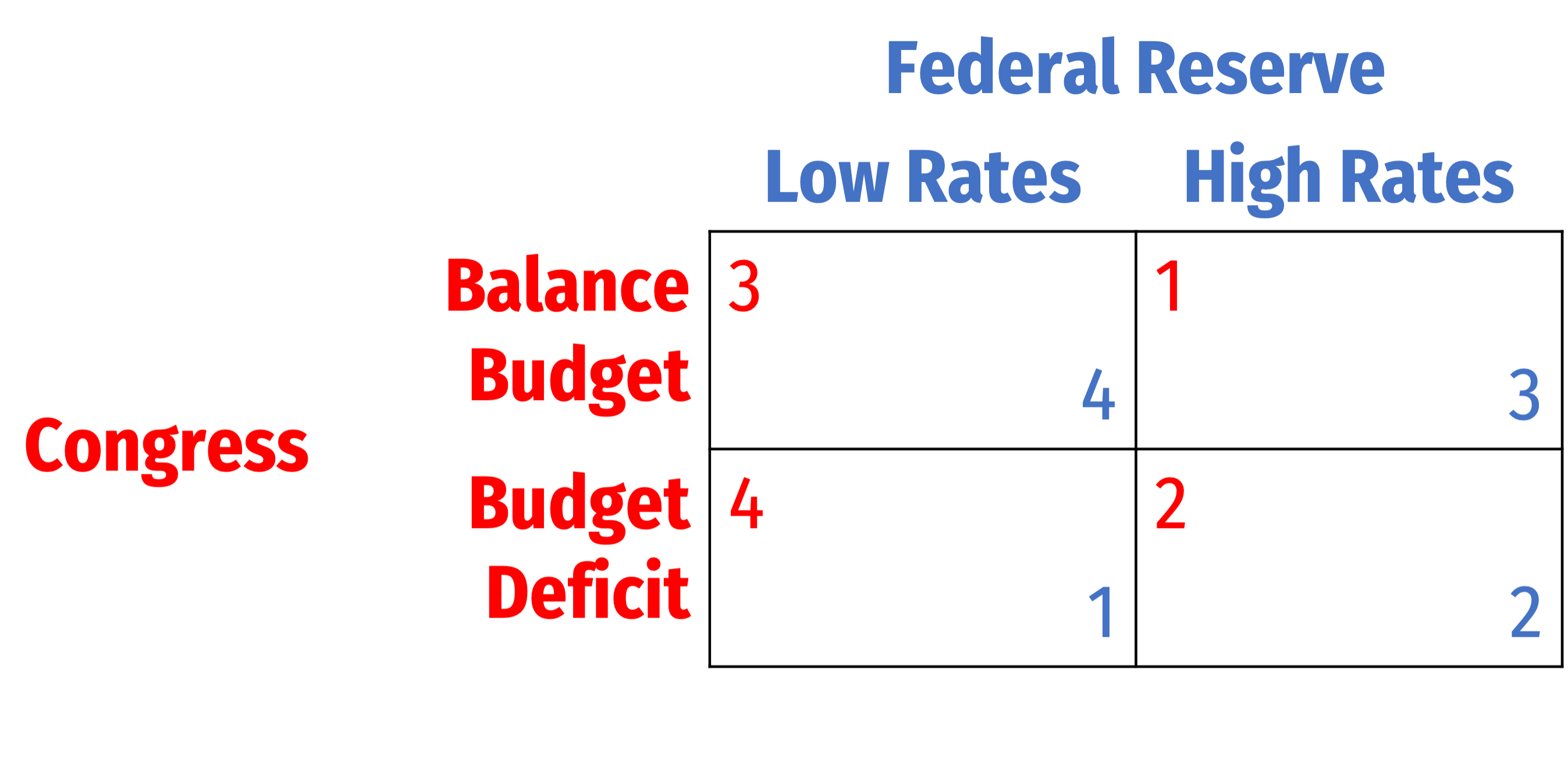
When One Player Has a Dominant Strategy

  • Both players choose policy simultaneously and independently of each other

  • How to find the equilibrium of this game?

    • Does the Fed have a dominant strategy?

When One Player Has a Dominant Strategy

  • Both players choose policy simultaneously and independently of each other

  • How to find the equilibrium of this game?

    • Does the Fed have a dominant strategy?
    • Does Congress?

When One Player Has a Dominant Strategy

  • Both players choose policy simultaneously and independently of each other

  • How to find the equilibrium of this game?

    • Does the Fed have a dominant strategy?
    • Does Congress?
    • Given this, how will Fed choose?

Successive Elimination of Dominated Strategies

  • What about the following game?

Successive Elimination of Dominated Strategies

  • What about the following game?

  • Hint: Do any of Row's strategies always yield a lower payoff than another strategy?

Successive Elimination of Dominated Strategies

  • What about the following game?

  • Hint: Do any of Row's strategies always yield a lower payoff than another strategy?

    • Down is dominated by Right

Successive Elimination of Dominated Strategies

  • What about the following game?

  • Hint: Do any of Row's strategies always yield a lower payoff than another strategy?

    • Down is dominated by Right
    • Remove this row, since Row will never play Down

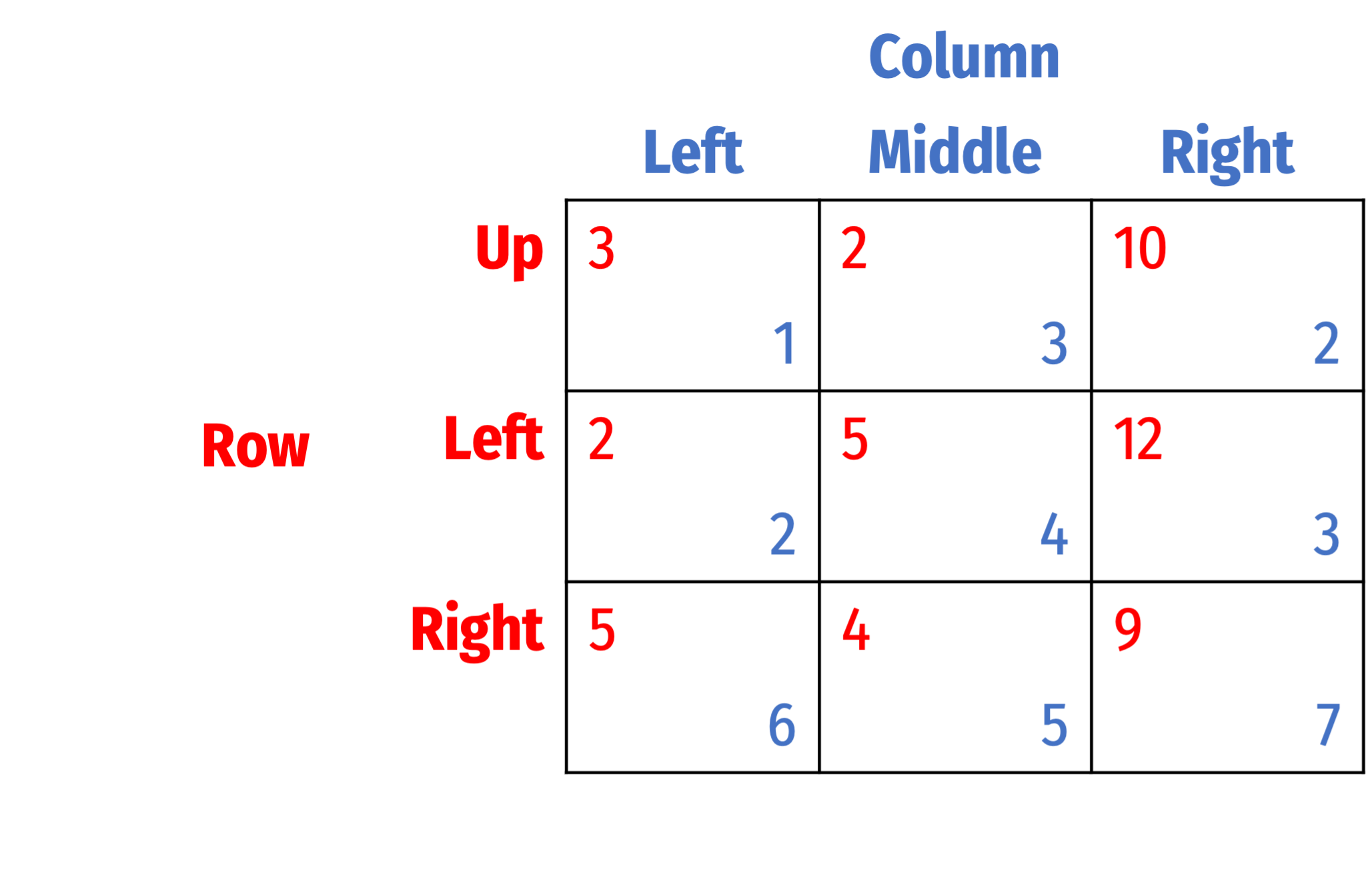
Successive Elimination of Dominated Strategies

  • Keep searching for dominated strategies...

  • Hint: Do any of Column's strategies always yield a lower payoff than another strategy?

Successive Elimination of Dominated Strategies

  • Keep searching for dominated strategies...

  • Hint: Do any of Column's strategies always yield a lower payoff than another strategy?

    • Left is dominated by Right
    • Remove this column, since Column will never play Left

Successive Elimination of Dominated Strategies

  • Keep searching for dominated strategies...

Successive Elimination of Dominated Strategies

  • Keep searching for dominated strategies...

  • For Row, Left dominates both Up and Right

    • Delete both Up and Right since Row will never play them

Successive Elimination of Dominated Strategies

  • Keep searching for dominated strategies...

  • Since Row will play Left, Column's best response is to play Middle

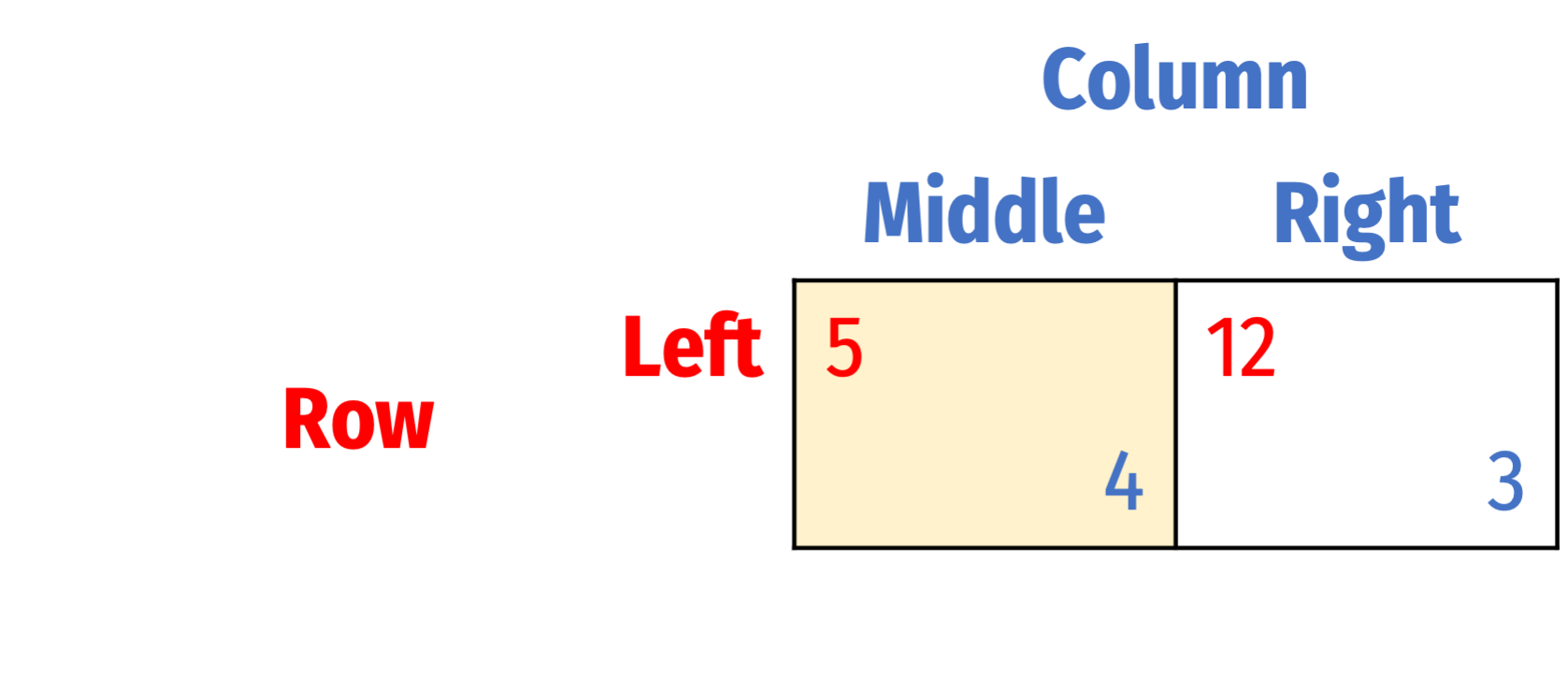
Successive Elimination of Dominated Strategies

  • We've found the Nash Equilibrium: (Left, Middle)

  • Check that it's truly an equilibrium

    • Does Row want to change from Left, given Column is playing Middle?
    • Does Column want to change from Middle, given Row is playing Left?

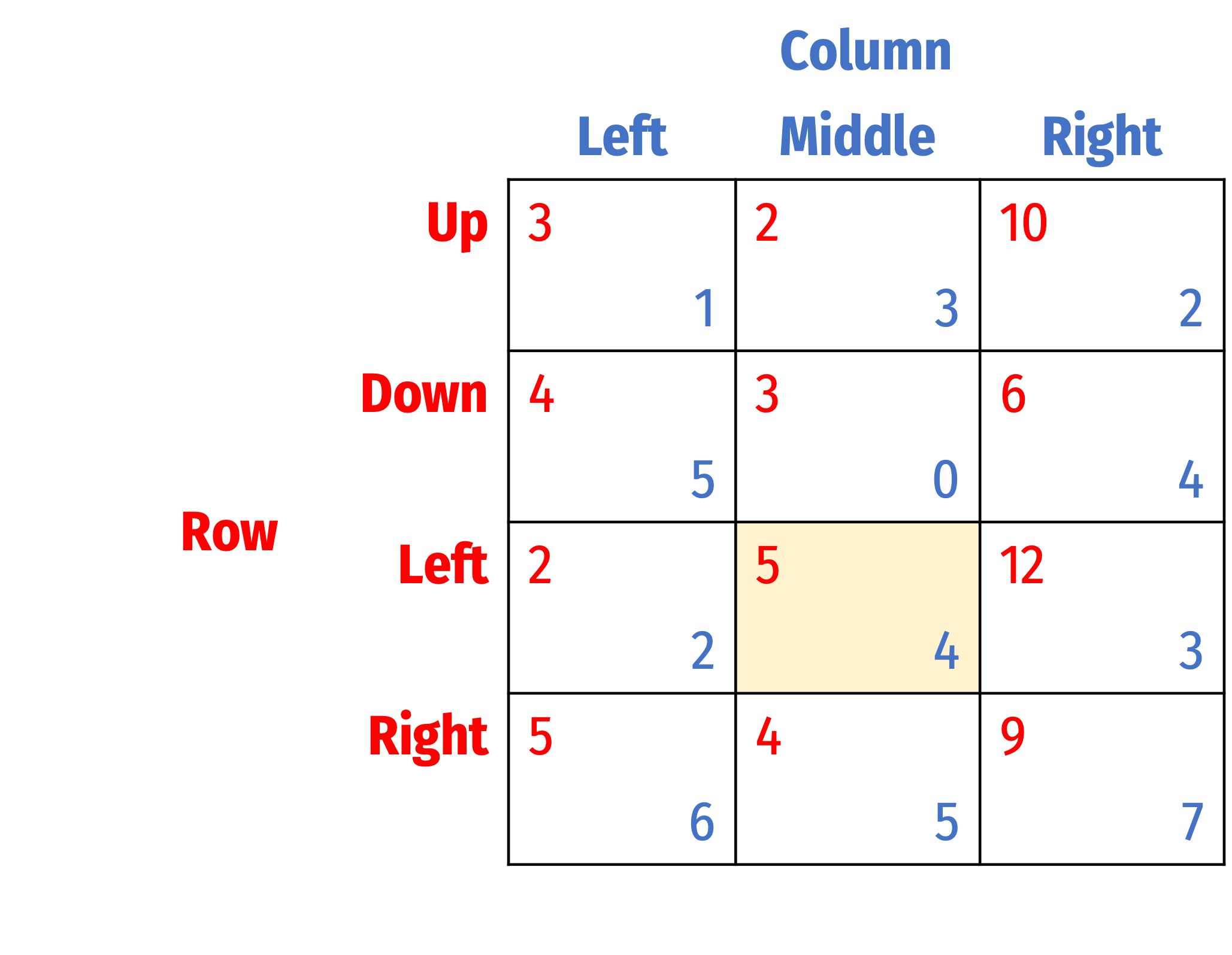
Successive Elimination of Dominated Strategies

  • If successive elimination of dominated strategies yields a unique outcome, then the game is “dominance solvable”
    • Not all games can be solved this way!

You Try

Eliminating Dominated Strategies: Not Foolproof

  • What about ties?

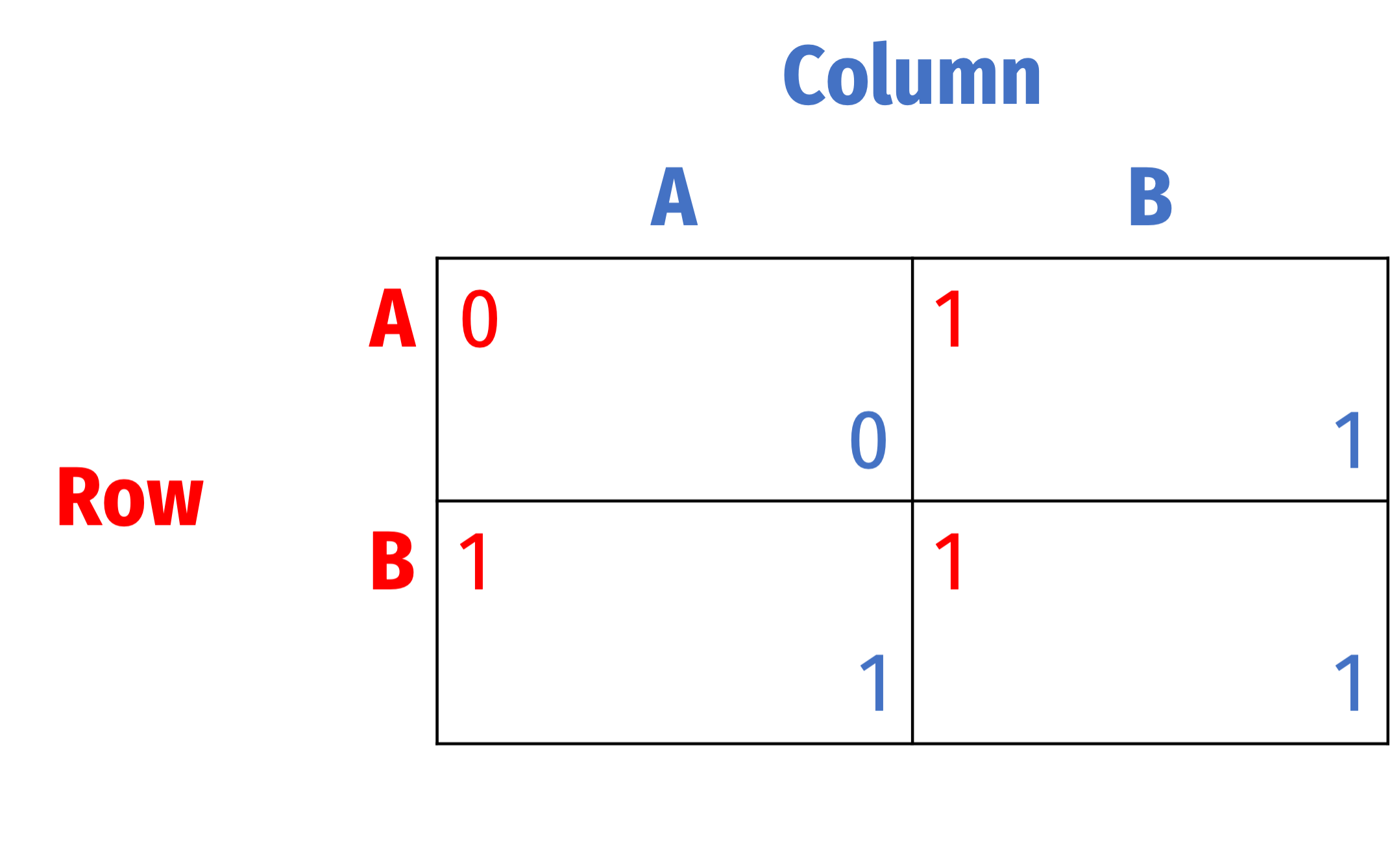
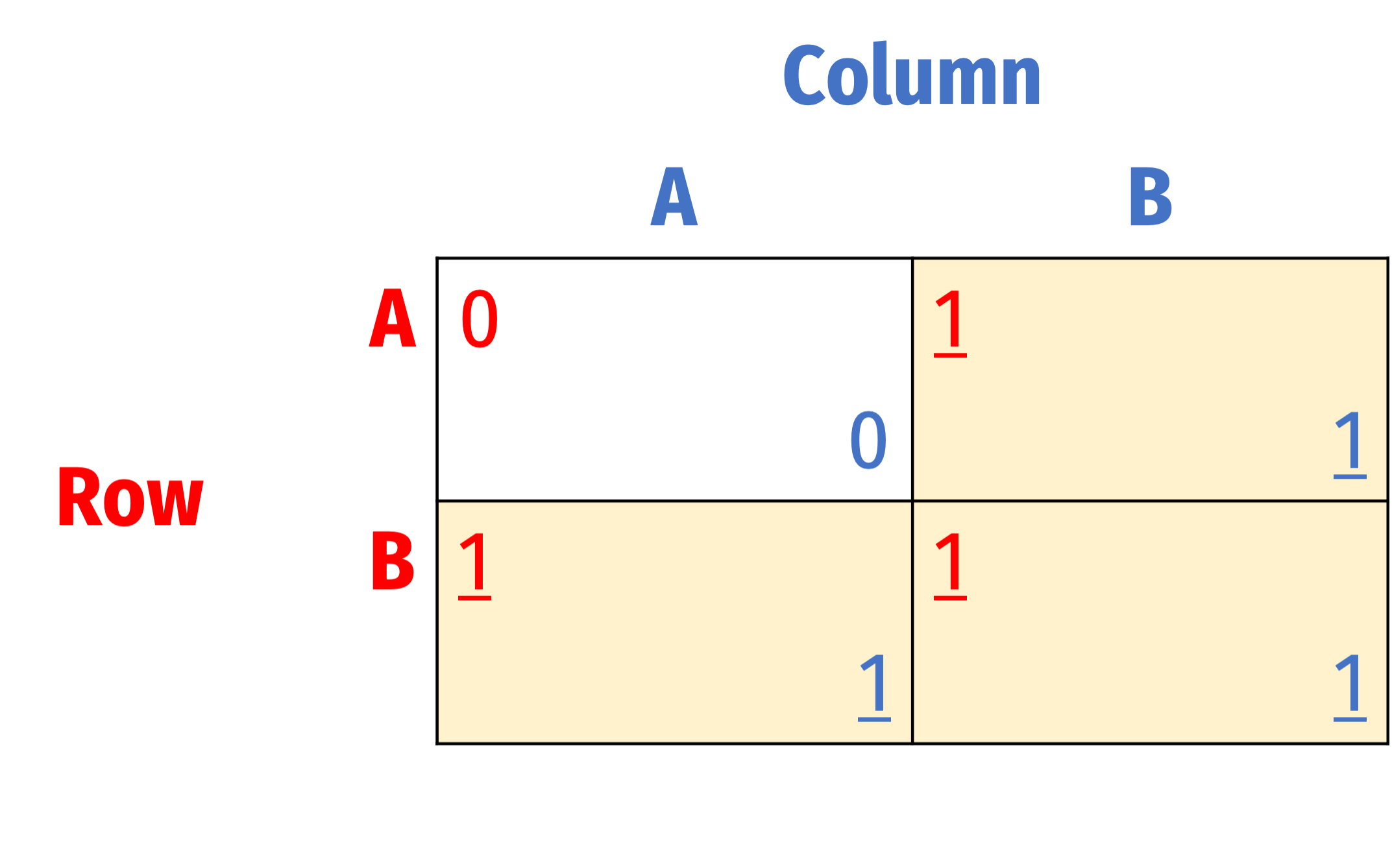
Eliminating Dominated Strategies: Not Foolproof

  • What about ties?

  • For Row, A is “weakly” dominated by B

    • If Column plays A, then playing B is strictly better than A for Row
    • If Column plays B, then playing B is at least as good (≿) as A for Row

Eliminating Dominated Strategies: Not Foolproof

  • What about ties?

  • Same for Column: A is “weakly” dominated by B

    • If Row plays A, then playing B is strictly better than A for Column
    • If Row plays B, then playing B is at least as good (≿) as A for Column

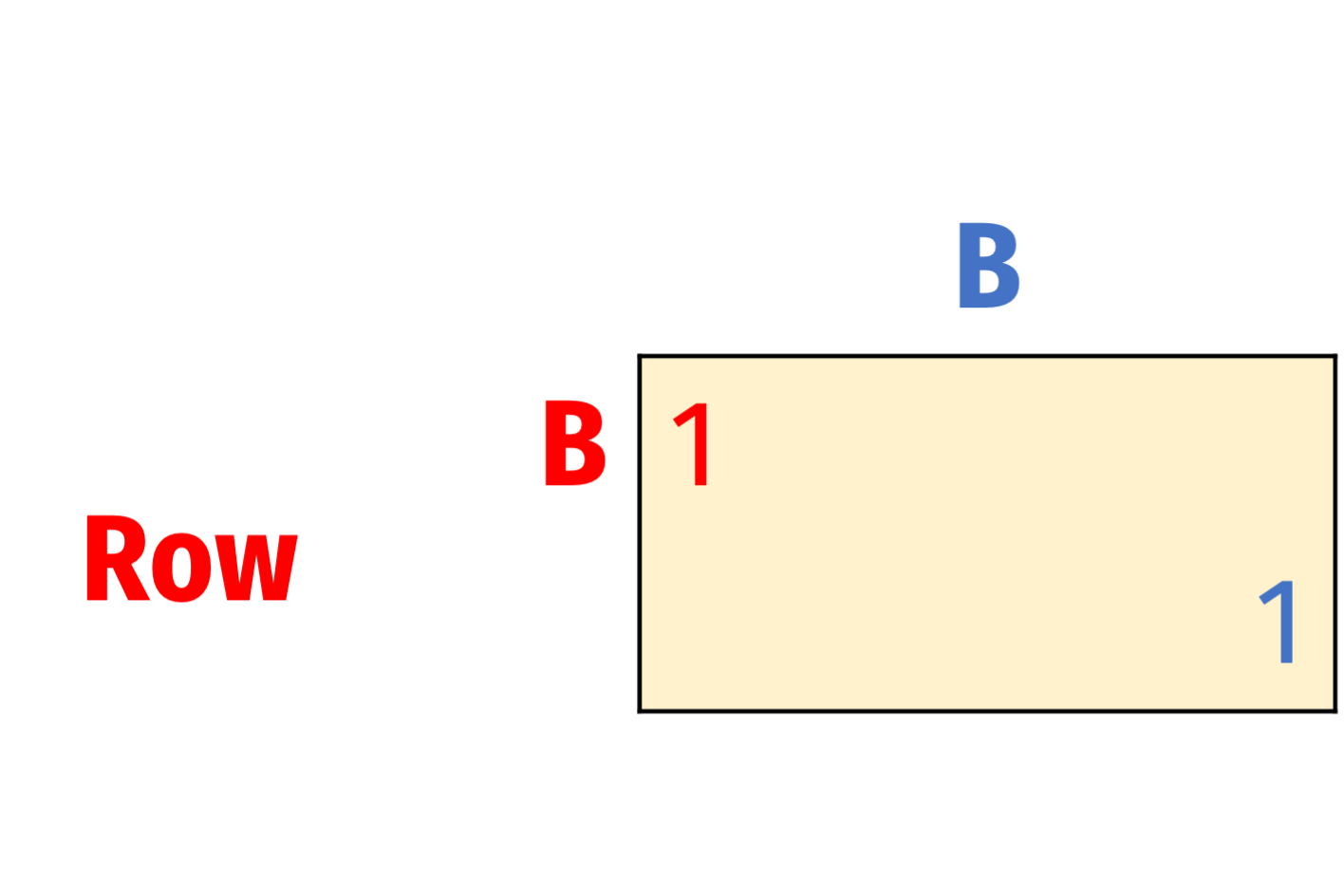
Eliminating Dominated Strategies: Not Foolproof

  • Successive elimination of weakly dominated strategies implies deleting A for both players

  • Predicted Nash Equilibrium: (B, B)

Eliminating Dominated Strategies: Not Foolproof

  • Successive elimination of weakly dominated strategies implies deleting A for both players

  • Predicted Nash Equilibrium: (B, B)

Eliminating Dominated Strategies: Not Foolproof

  • Successive elimination of weakly dominated strategies implies deleting A for both players

  • Predicted Nash Equilibrium: (B, B)

  • But (A, B) and (B, A) are also Nash equilibria!

    • Check for yourself

  • So we can only rule out strictly dominated strategies!

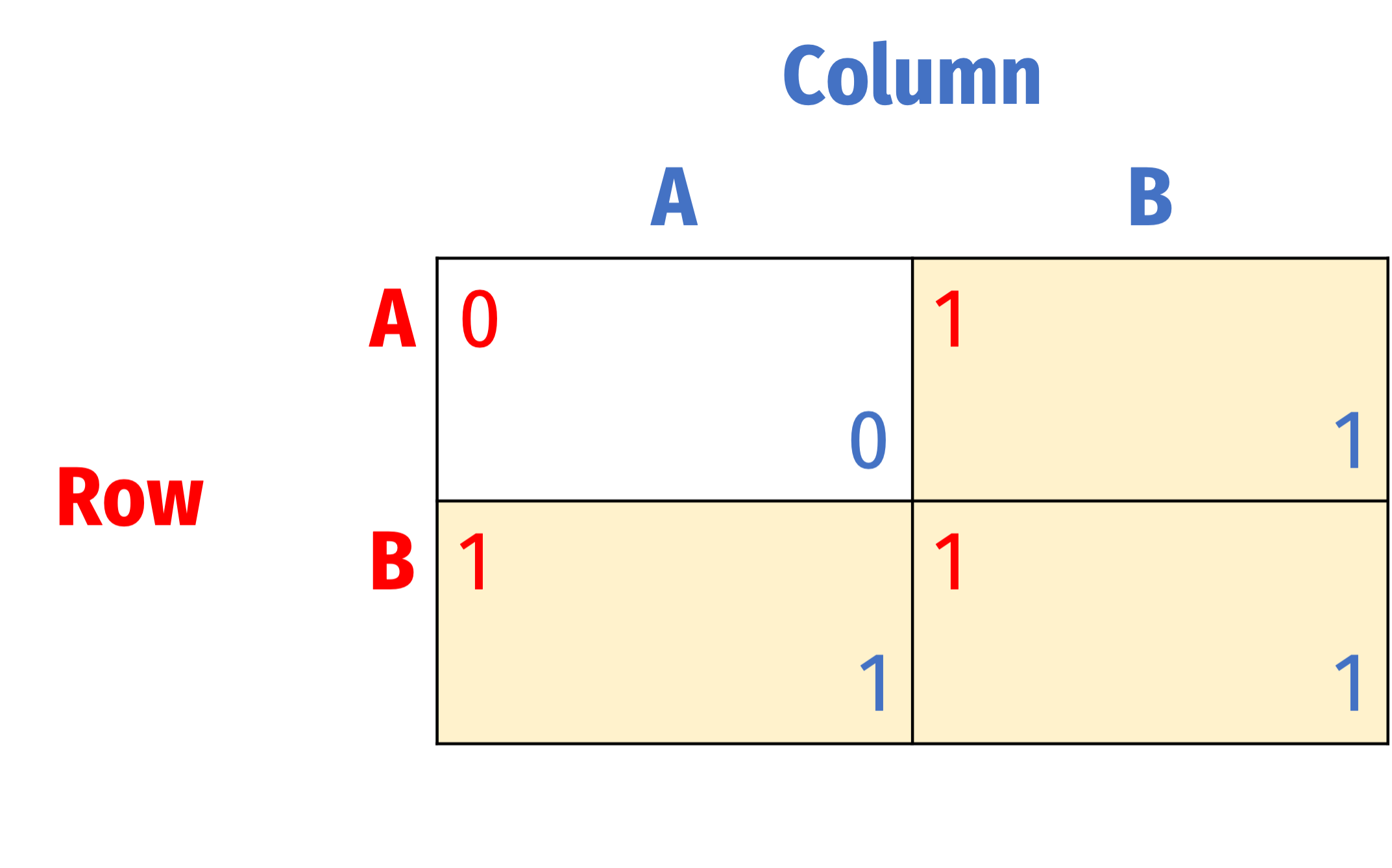
Best Response Analysis

Best Response Analysis

  • Consider this game again, and check for each player’s best response to each of the other player's strategies

Best Response Analysis

  • Consider Row
    • If Column plays Left

Best Response Analysis

  • Consider Row
    • If Column plays Left, best response is Right

Best Response Analysis

  • Consider Row
    • If Column plays Left, best response is Right
    • If Column plays Middle, best response is Left

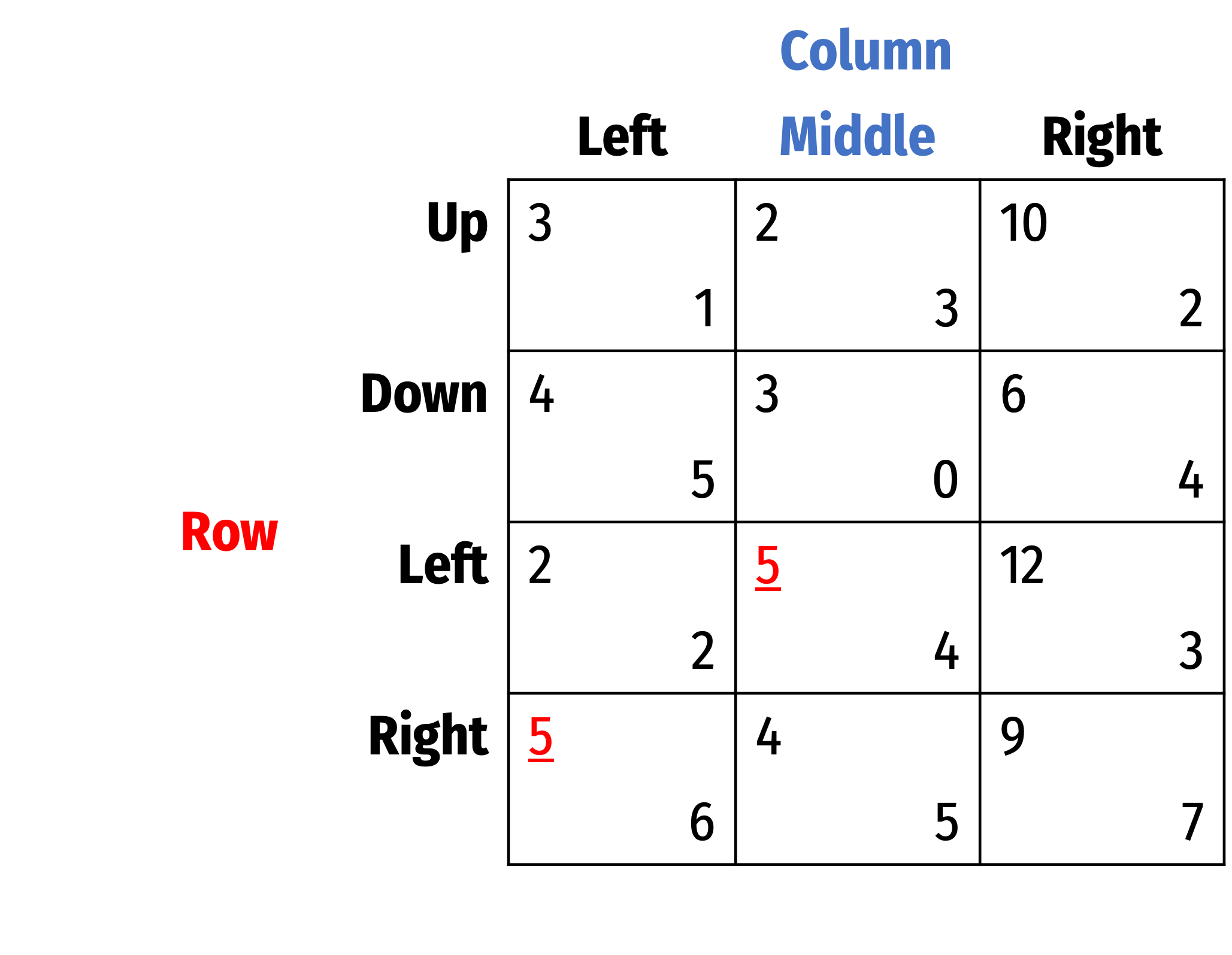
Best Response Analysis

  • Consider Row
    • If Column plays Left, best response is Right
    • If Column plays Middle, best response is Left
    • If Column plays Right, best response is Left

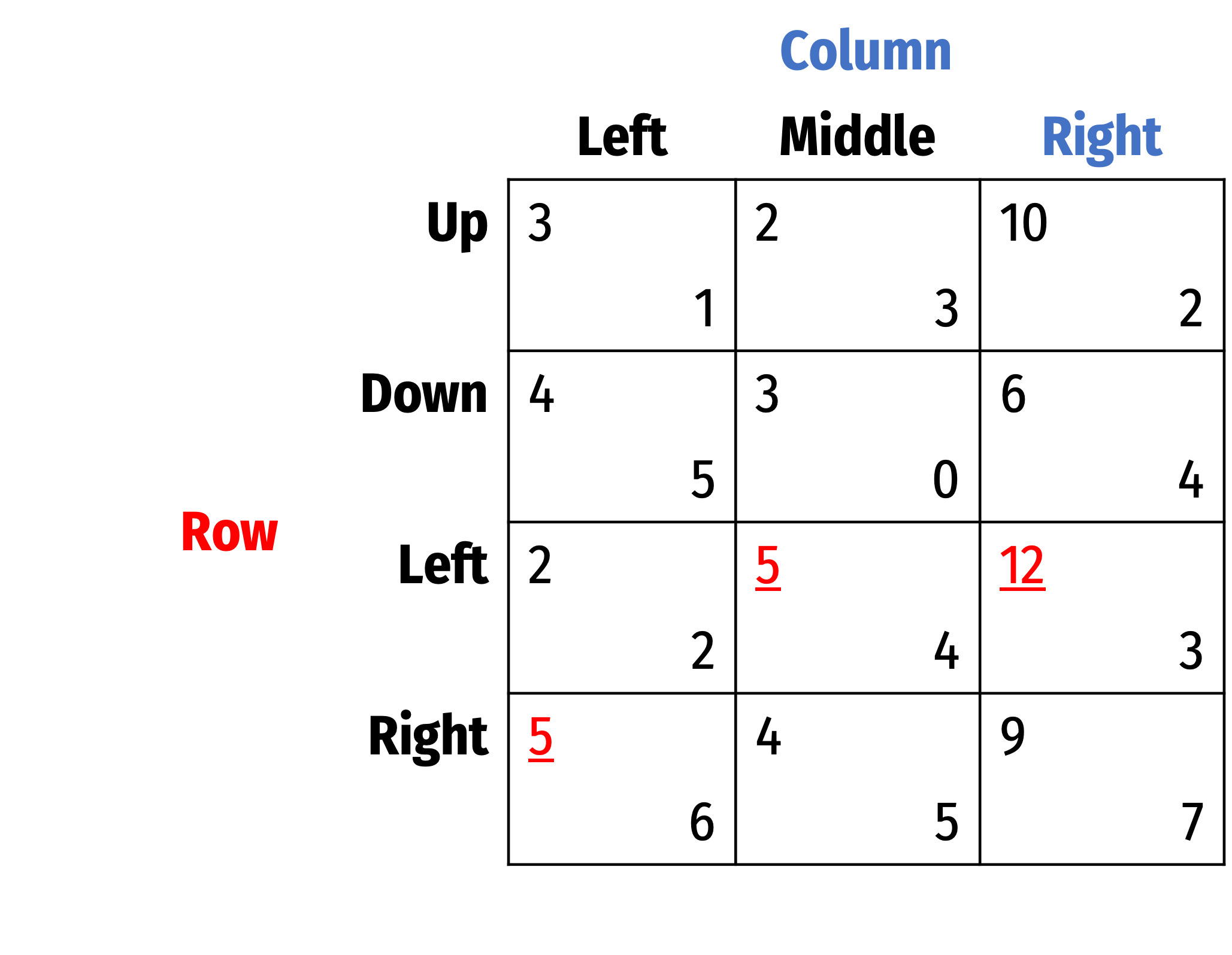
Best Response Analysis

  • Consider Column
    • If Row plays Up

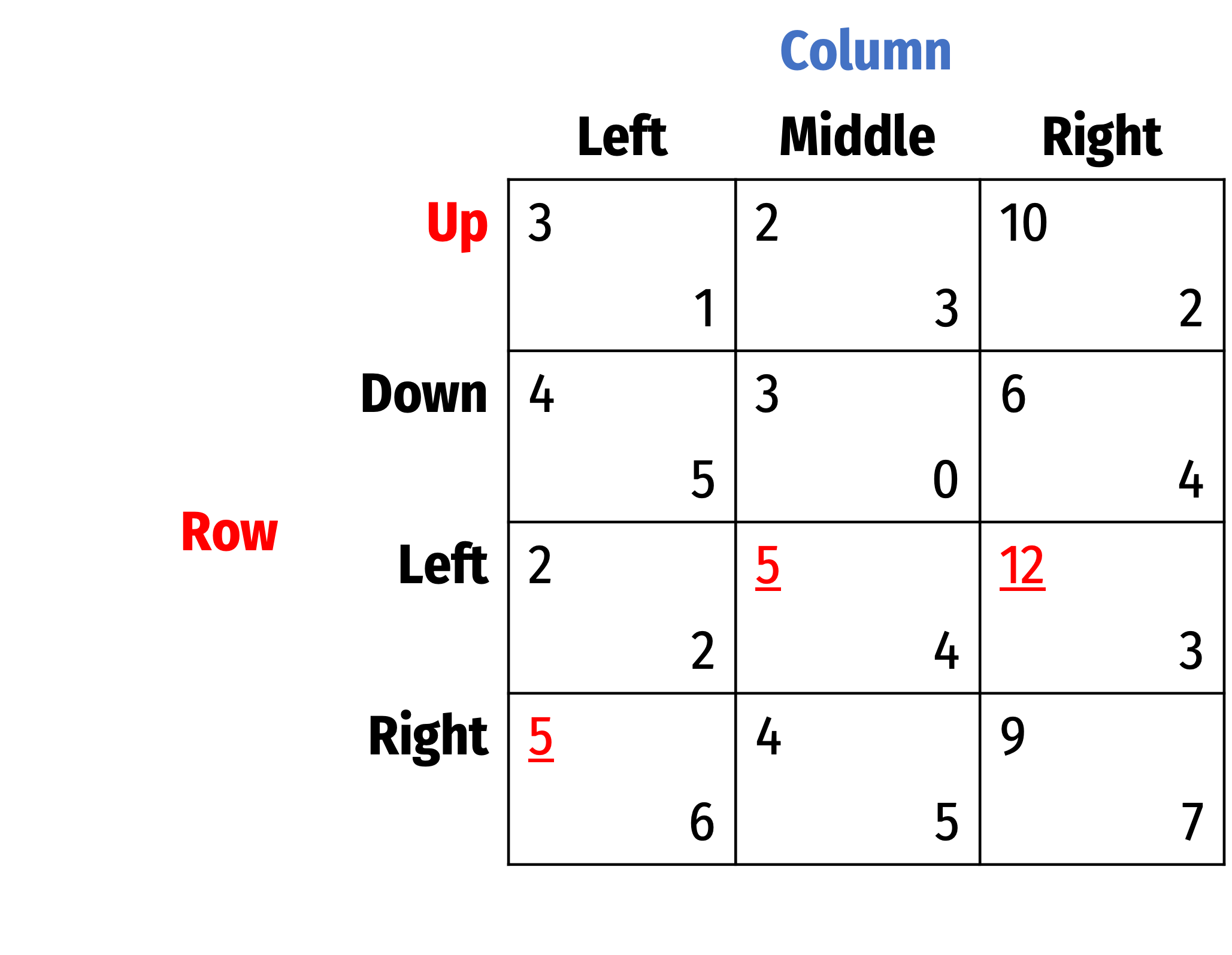
Best Response Analysis

  • Consider Column
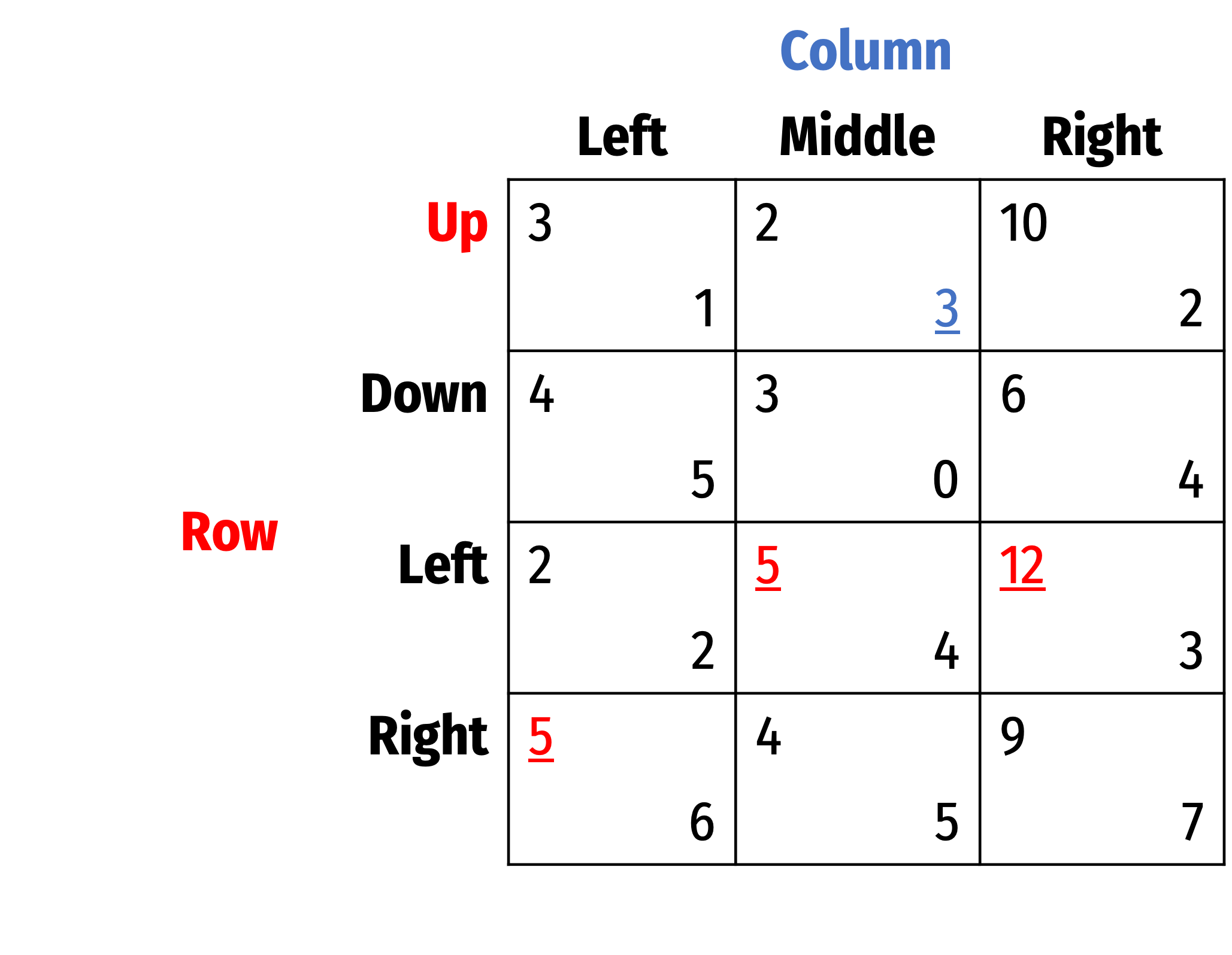
    • If Row plays Up, best response is Middle

Best Response Analysis

  • Consider Column
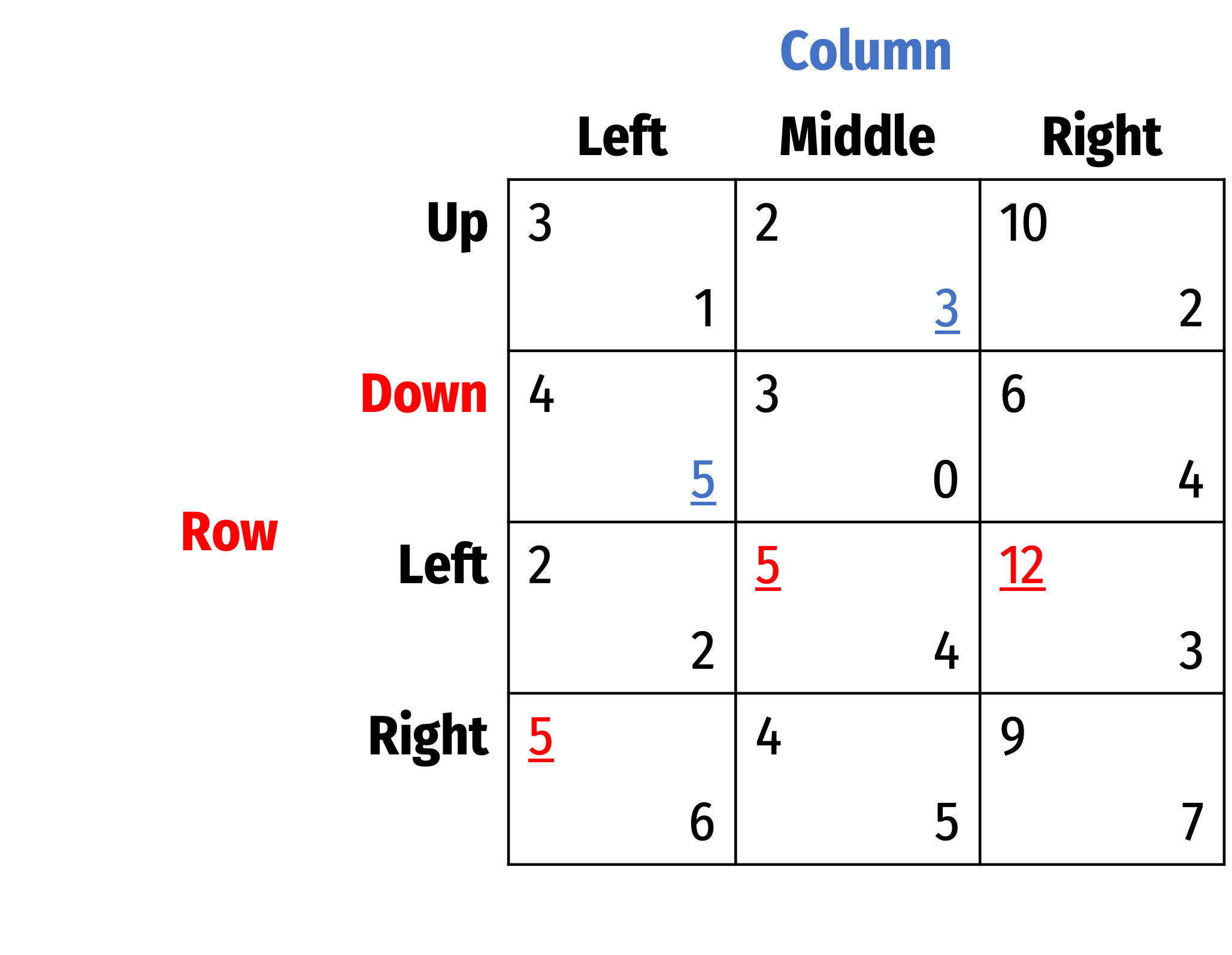
    • If Row plays Up, best response is Middle
    • If Row plays Down, best response is Left

Best Response Analysis

  • Consider Column
    • If Row plays Up, best response is Middle
    • If Row plays Down, best response is Left
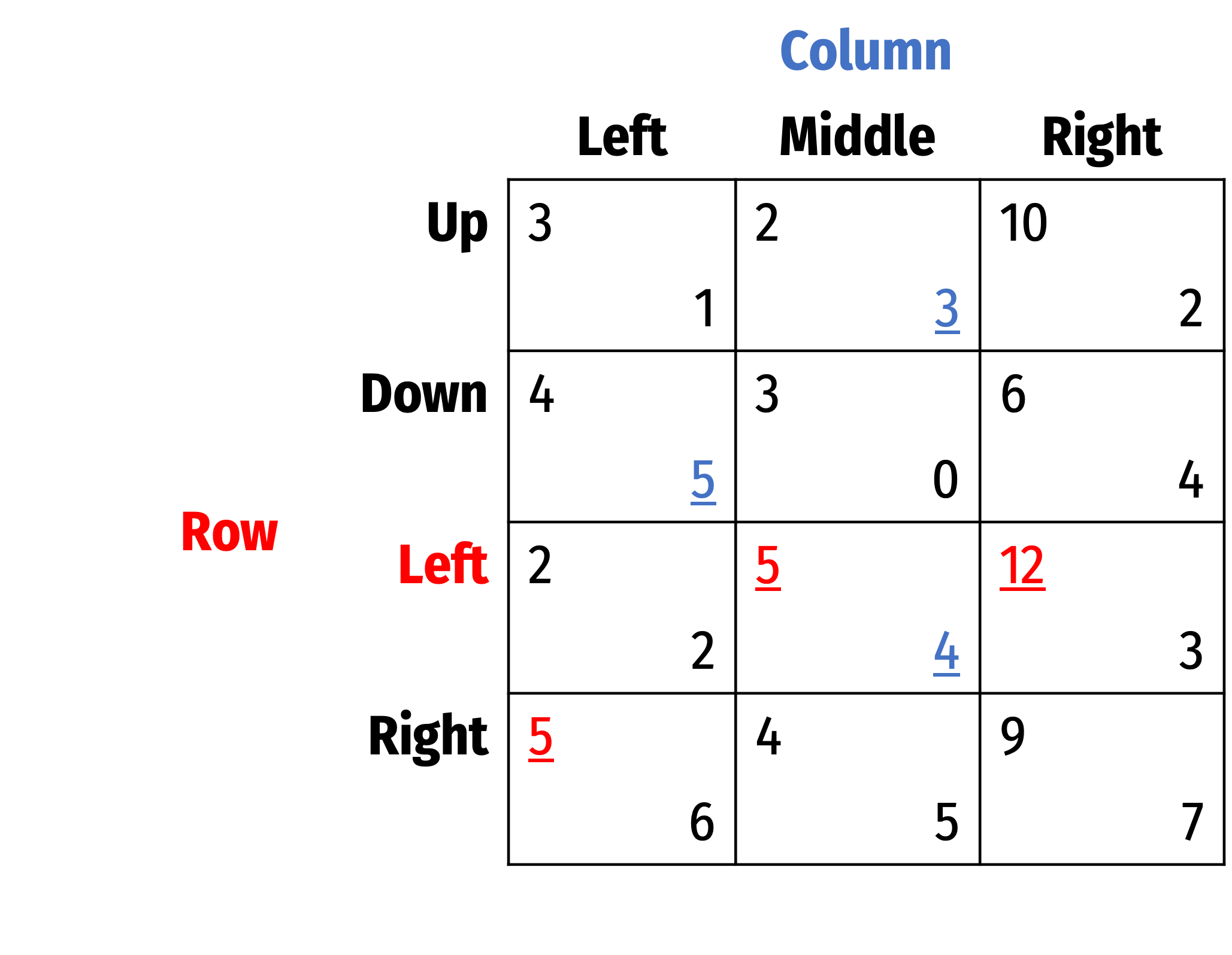
    • If Row plays Left, best response is Middle

Best Response Analysis

  • Consider Column
    • If Row plays Up, best response is Middle
    • If Row plays Down, best response is Left
    • If Row plays Left, best response is Middle
    • If Row plays Right, best response is Right

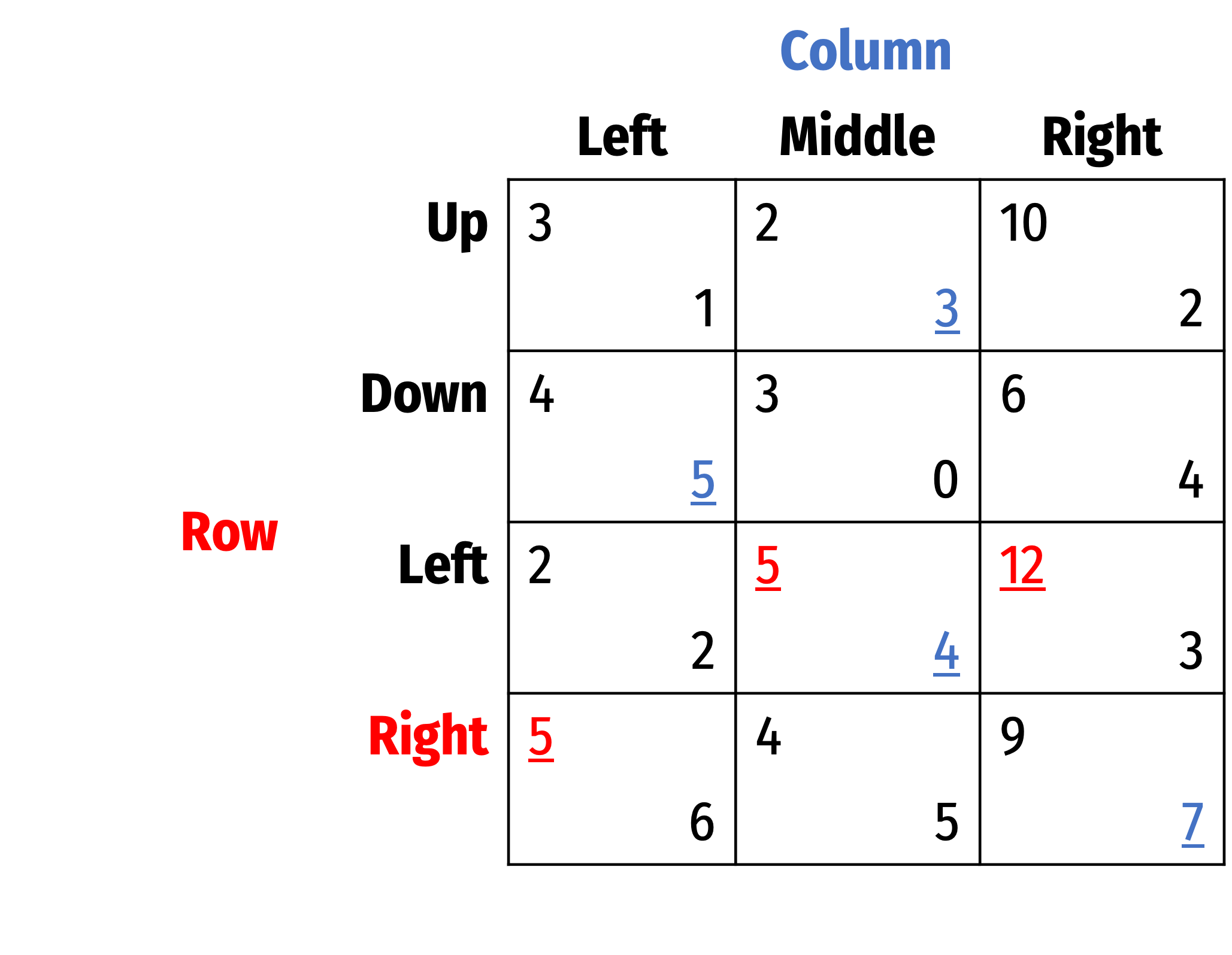
Best Response Analysis

  • Highlighted all best responses for each player, shows us the Nash Equilibrium: (Left, Middle)

  • In a Nash equilibrium, all players are playing a best response to each other's strategies

  • A more tedious process, but foolproof

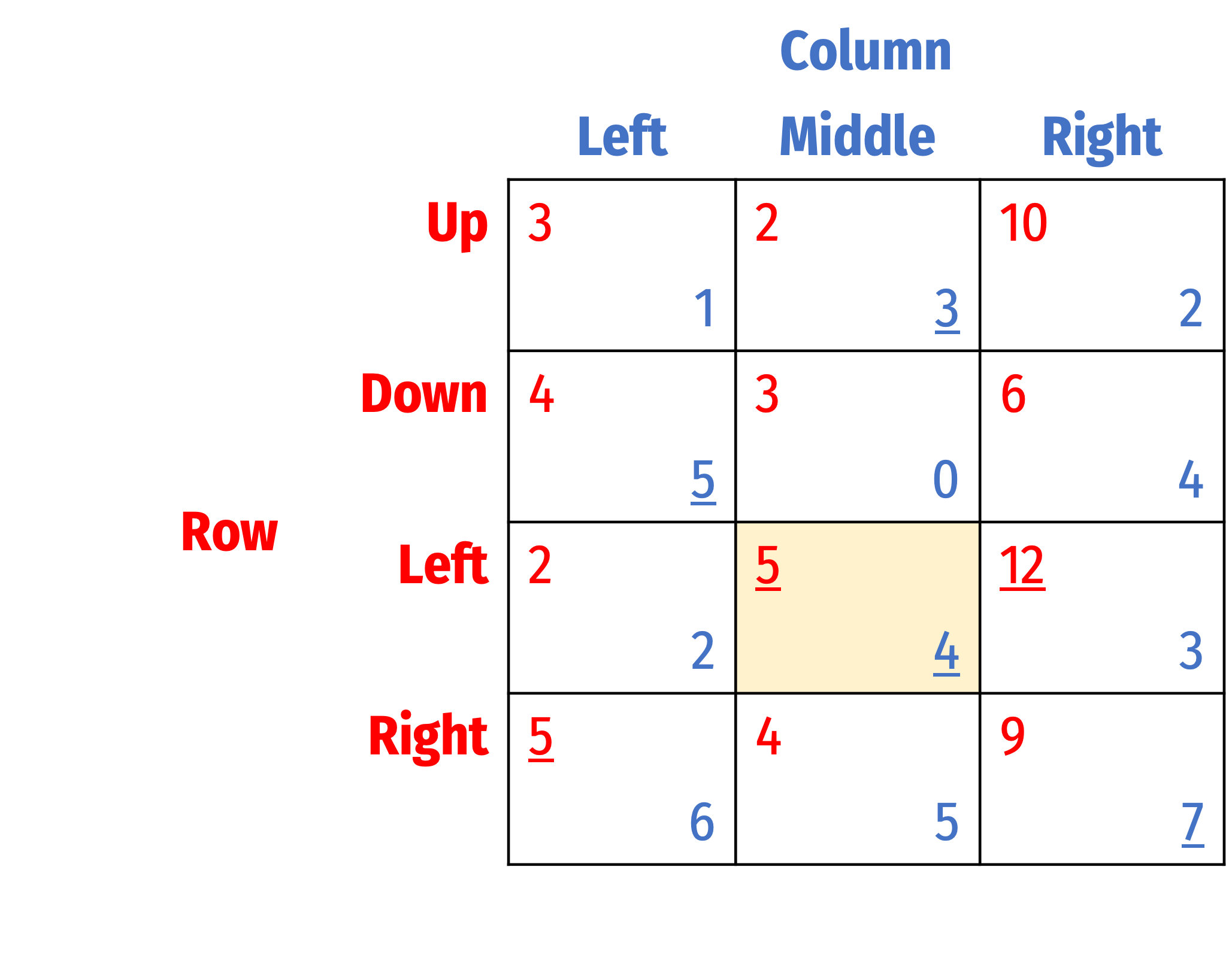
Best Response Analysis Permits Ties

  • For Row in this game:

    • If Column plays A, Row's best response is B
    • If Column plays B, A and B are both best responses

  • Symmetrically for Column

  • Finds all three Nash equilibria (in each, both players play a best response)

    1. (B, A)
    2. (A, B)
    3. (B, B)

Depicting Three Player Games

Depicting Three Player Games

  • Represent ABC's choice across two matrices
  • Three payoffs for each outcome: (CBS, NBC, ABC)
  • Let's first try solving by searching for dominated strategies...

Depicting Three Player Games

  • Represent ABC's choice across two matrices
  • Three payoffs for each outcome: (CBS, NBC, ABC)

  • Let's first try solving by searching for dominated strategies...

  • Game Show is dominated by Sitcom for ABC, so delete it

Depicting Three Player Games

  • Keep searching

Depicting Three Player Games

  • Keep searching

  • Sitcom is dominated by Game Show for NBC, so delete it

Depicting Three Player Games

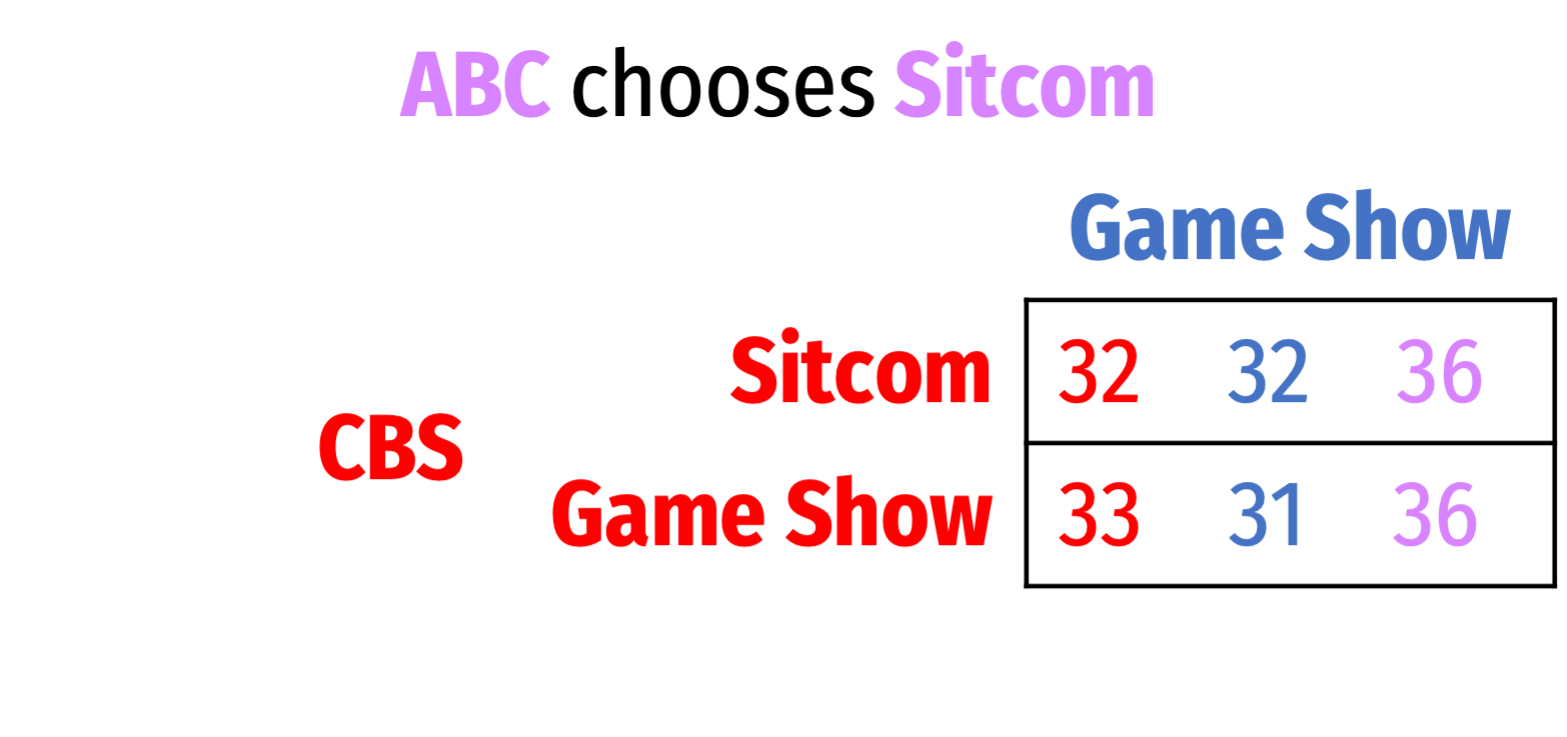
  • Keep searching

Depicting Three Player Games

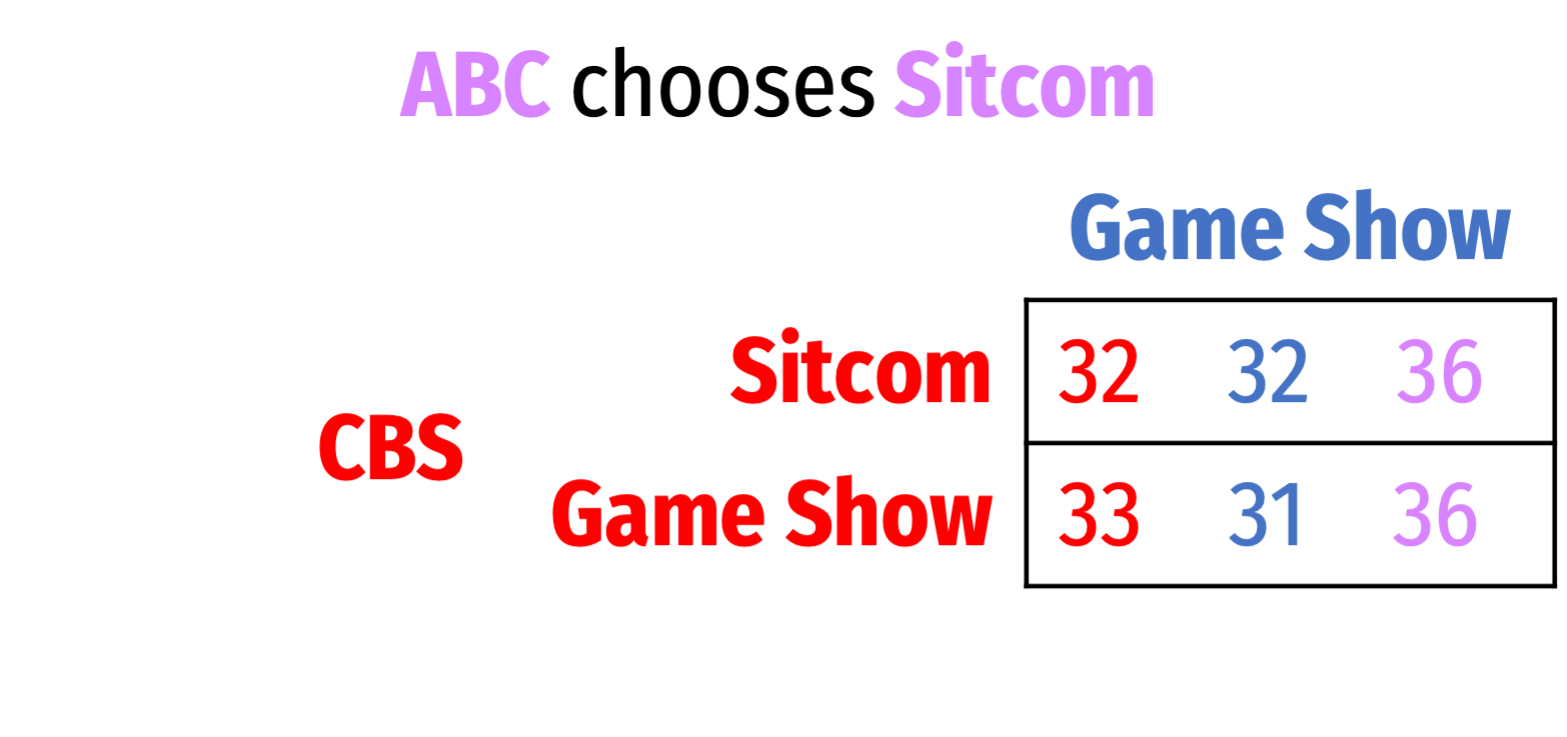
  • Keep searching

  • Sitcom is dominated by Game Show for CBS, so delete it

Depicting Three Player Games

  • Nash Equilibrium: (Game Show, Game Show, Sitcom)

Depicting Three Player Games

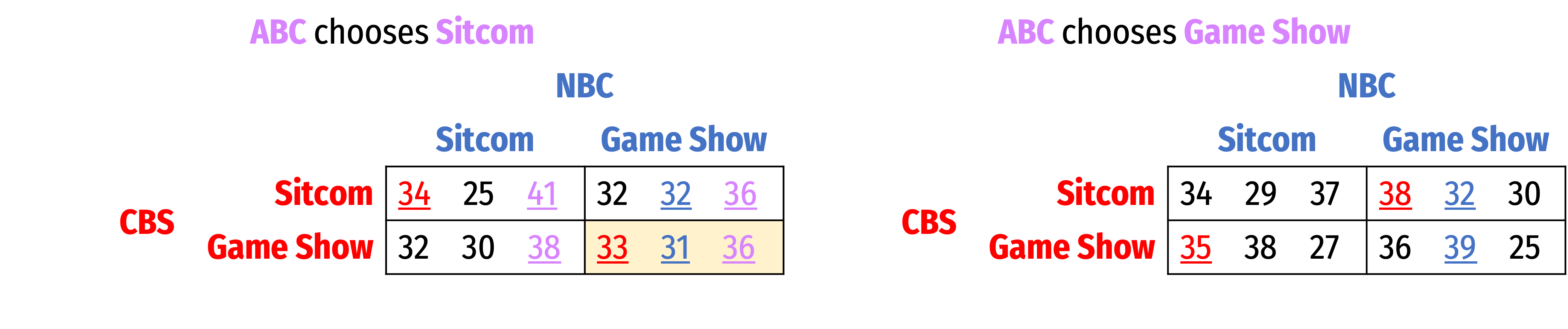
  • Nash Equilibrium: (Game Show, Game Show, Sitcom)

Depicting Three Player Games

  • Nash Equilibrium: (Game Show, Game Show, Sitcom)

  • Now let's try using best response analysis instead

Depicting Three Player Games

  • Start with CBS
    • If NBC chooses Sitcom and ABC chooses Sitcom

Depicting Three Player Games

  • Start with CBS
    • If NBC chooses Sitcom and ABC chooses Sitcom, CBS' BR: Sitcom

Depicting Three Player Games

  • Start with CBS
    • If NBC chooses Sitcom and ABC chooses Sitcom, CBS' BR: Sitcom
    • If NBC chooses Game Show and ABC chooses Sitcom, CBS' BR: Game Show

Depicting Three Player Games

  • Start with CBS
    • If NBC chooses Sitcom and ABC chooses Sitcom, CBS' BR: Sitcom
    • If NBC chooses Game Show and ABC chooses Sitcom, CBS' BR: Game Show
    • If NBC chooses Sitcom and ABC chooses Game Show, CBS' BR: Game Show

Depicting Three Player Games

  • Start with CBS
    • If NBC chooses Sitcom and ABC chooses Sitcom, CBS' BR: Sitcom
    • If NBC chooses Game Show and ABC chooses Sitcom, CBS' BR: Game Show
    • If NBC chooses Sitcom and ABC chooses Game Show, CBS' BR: Game Show
    • If NBC chooses Game Show and ABC chooses Game Show, CBS' BR: Sitcom

Depicting Three Player Games

  • Now consider NBC

Depicting Three Player Games

  • Now consider NBC
    • If CBS chooses Sitcom and ABC chooses Sitcom, NBC's BR: Game Show

Depicting Three Player Games

  • Now consider NBC
    • If CBS chooses Sitcom and ABC chooses Sitcom, NBC's BR: Game Show
    • If CBS chooses Game Show and ABC chooses Sitcom, NBC's BR: Game Show

Depicting Three Player Games

  • Now consider NBC
    • If CBS chooses Sitcom and ABC chooses Sitcom, NBC's BR: Game Show
    • If CBS chooses Game Show and ABC chooses Sitcom, NBC's BR: Game Show
    • If CBS chooses Sitcom and ABC chooses Game Show, NBC's BR: Game Show

Depicting Three Player Games

  • Now consider NBC
    • If CBS chooses Sitcom and ABC chooses Sitcom, NBC's BR: Game Show
    • If CBS chooses Game Show and ABC chooses Sitcom, NBC's BR: Game Show
    • If CBS chooses Sitcom and ABC chooses Game Show, NBC's BR: Game Show
    • If CBS chooses Game Show and ABC chooses Game Show, NBC's BR: Game Show

Depicting Three Player Games

  • Finally consider ABC

Depicting Three Player Games

  • Finally consider ABC
    • If CBS chooses Sitcom and NBC chooses Sitcom, ABC's BR: Sitcom

Depicting Three Player Games

  • Finally consider ABC
    • If CBS chooses Sitcom and NBC chooses Sitcom, ABC's BR: Sitcom
    • If CBS chooses Game Show and NBC chooses Sitcom, ABC's BR: Sitcom

Depicting Three Player Games

  • Finally consider ABC
    • If CBS chooses Sitcom and NBC chooses Sitcom, ABC's BR: Sitcom
    • If CBS chooses Game Show and NBC chooses Sitcom, ABC's BR: Sitcom
    • If CBS chooses Sitcom and NBC chooses Game Show, ABC's BR: Sitcom

Depicting Three Player Games

  • Finally consider ABC
    • If CBS chooses Sitcom and NBC chooses Sitcom, ABC's BR: Sitcom
    • If CBS chooses Game Show and NBC chooses Sitcom, ABC's BR: Sitcom
    • If CBS chooses Sitcom and NBC chooses Game Show, ABC's BR: Sitcom
    • If CBS chooses Game Show and NBC chooses Game Show, ABC's BR: Sitcom

Depicting Three Player Games

  • Nash Equilibrium: (Game Show, Game Show, Sitcom)

Summary of Methods of Finding Nash Eq.

Ranked from (most to least) effective and (most to least) tedious:

  1. Cell-by-cell inspection

    • For each outcome, ask: would any player like to change strategy given others' strategies?
    • Every outcome where all players answer “NO” is a Nash equilibrium

  2. Best response analysis

    • For each possible strategy of other players, what is a player's best response?
    • If all players are playing a best response in an outcome, that's a Nash equilibrium

  3. Successive elimination of dominated strategies

    • Eliminate (dominated) strategies players will never play
    • If a single strategy remains for each player, that's the Nash equilibrium
    • Ties cause you to rule out potential Nash equilibria!

Outline

Games in Normal Form

Dominance-Solvability

Best-Response

Depicting Three Player Games

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
oTile View: Overview of Slides
Esc Back to slideshow