2.2 — Bertrand Competition
ECON 316 • Game Theory • Fall 2021
Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/gameF21
gameF21.classes.ryansafner.com
A More Rigorous Oligopoly/Cartel Problem
Example: Suppose Squeaky Clean (Firm 1) and Biobase (Firm 2) are the only two producers of chlorine for swimming pools. The inverse market demand for chlorine is P=32−2Q
If the two firms collude and agree to act as a monopolist and evenly split the market, how much will each firm produce, what will be the market price, and how much profit will each firm earn?
Under this agreement, does either firm have an incentive to cheat (i.e. by producing an additional ton of chlorine)? What would happen to each firm's profits if either, or both, cheated?
Bertrand Competition: Moblab

Bertrand Competition: Moblab
Each of you are selling identical Economics 101 course notes
You will be randomly put into a market with 1 other player
Each term, both of you simultaneously choose your price
Seller(s) choosing the lowest price get all the customers

Bertrand Competition: Moblab
The lowest price pL determines the market demand q=3600−200pL
Both firms have $2 cost per unit sold
p=10 maximizes total market profits

Bertrand Competition: Moblab
q=3600−200pL
Example:
Suppose Firm 1 sets p=9 and Firm 2 sets p=10
Firm 2 sells 0, makes $0 profit
Firm 1 sells q=3,600−200(9)=1,800 and earns 1,800(9−2)=12,600 profit

Models of Oligopoly
Three canonical models of Oligopoly
- Bertrand competition
- Firms simultaneously compete on price
- Cournot competition
- Firms simultaneously compete on quantity
- Stackelberg competition
- Firms sequentially compete on quantity

Bertrand Competition
Joseph Bertrand
1822-1890
"Bertrand competition": two (or more) firms compete on price to sell the same good
Firms set their prices simultaneously
Consumers are indifferent between the brands and always buy from the seller with the lowest price
Bertrand Competition: Example
Suppose two firms, Walmart and Target stock and sell identical HDTVs
Costs each firm $200 to stock an HDTV
Let Q be the total quantity purchased by consumers from the entire market (i.e. both firms)
- Q=qw+qt
Denote Walmart's price as pw and Target's price as pt

Bertrand Competition: Example
- Demand for HDTV's at Walmart:
Bertrand Competition: Example
- Demand for HDTV's at Walmart:
- Q if pw < pt
Bertrand Competition: Example
- Demand for HDTV's at Walmart:
- Q if pw < pt
- Q2 if pw = pt
Bertrand Competition: Example
- Demand for HDTV's at Walmart:
- Q if pw < pt
- Q2 if pw = pt
- 0 if pw > pt
Bertrand Competition: Example
- Demand for HDTV's at Walmart:
- Q if pw < pt
- Q2 if pw = pt
- 0 if pw > pt
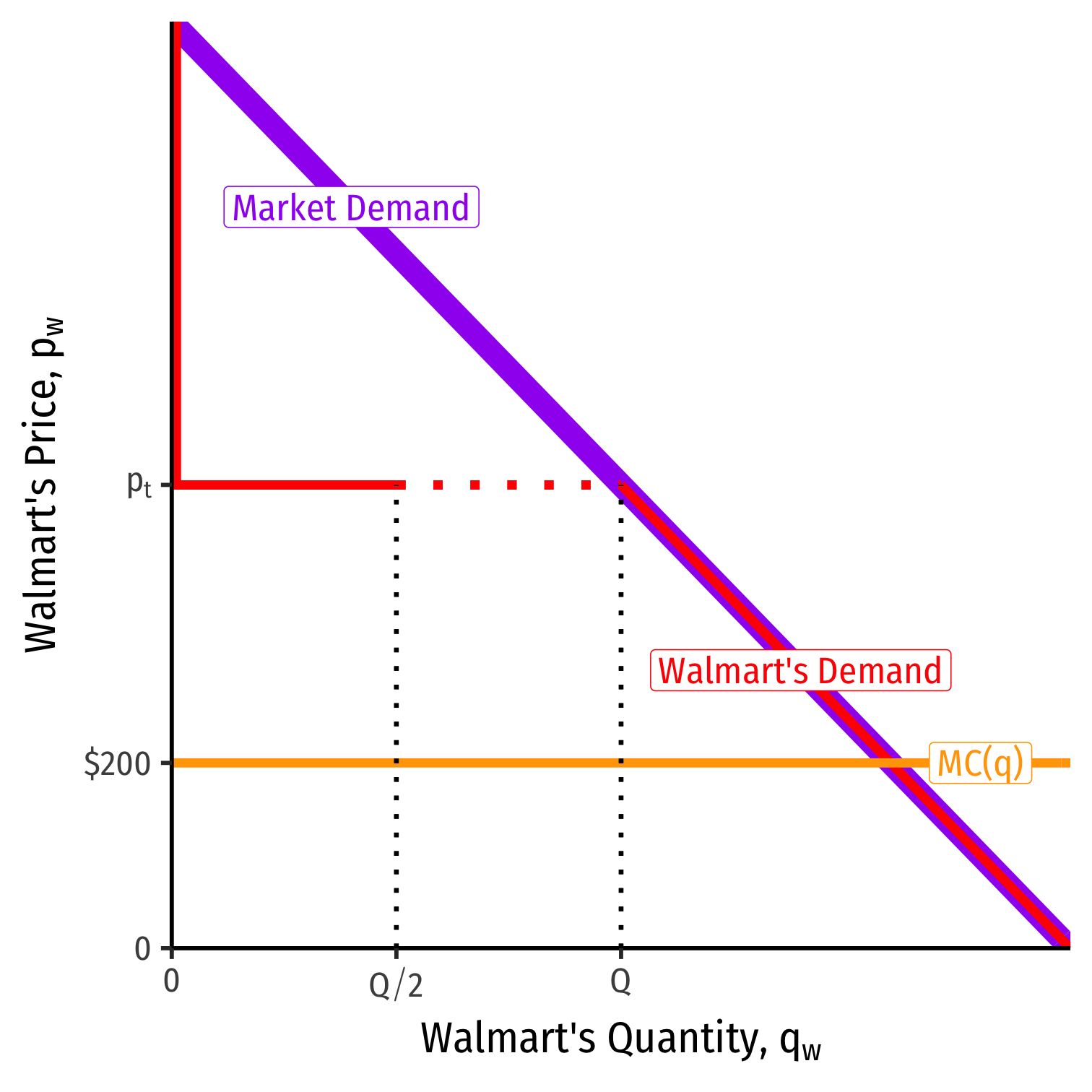
Bertrand Competition: Example
- Demand for HDTV's at Walmart:
- Q if pw < pt
- Q2 if pw = pt
- 0 if pw > pt
- Demand for HDTV's at Target:
- 0 if pw < pt
- Q2 if pw = pt
- Q if pw > pt
Bertrand Competition: Example
- The only way to sell TVs is to match or beat your competitor's price

Bertrand Competition: Example
The only way to sell TVs is to match or beat your competitor's price
Suppose you are Walmart
For a known pt, setting your price
pw=pt−ϵ
for any arbitrary ϵ>0 captures you the entire market Q
- Same for Target for pw

Bertrand Competition: Example
Won't charge p<MC, earn losses
Firms continue undercutting one another until pw = pt =MC
Nash Equilibrium: (pw=MC,pt=MC)
- Firms earn no profits!

Bertrand Paradox
- Bertrand Paradox: competitive outcome can be achieved with just 2 firms!
- p=MC, π=0

Walmart's Reaction Curve
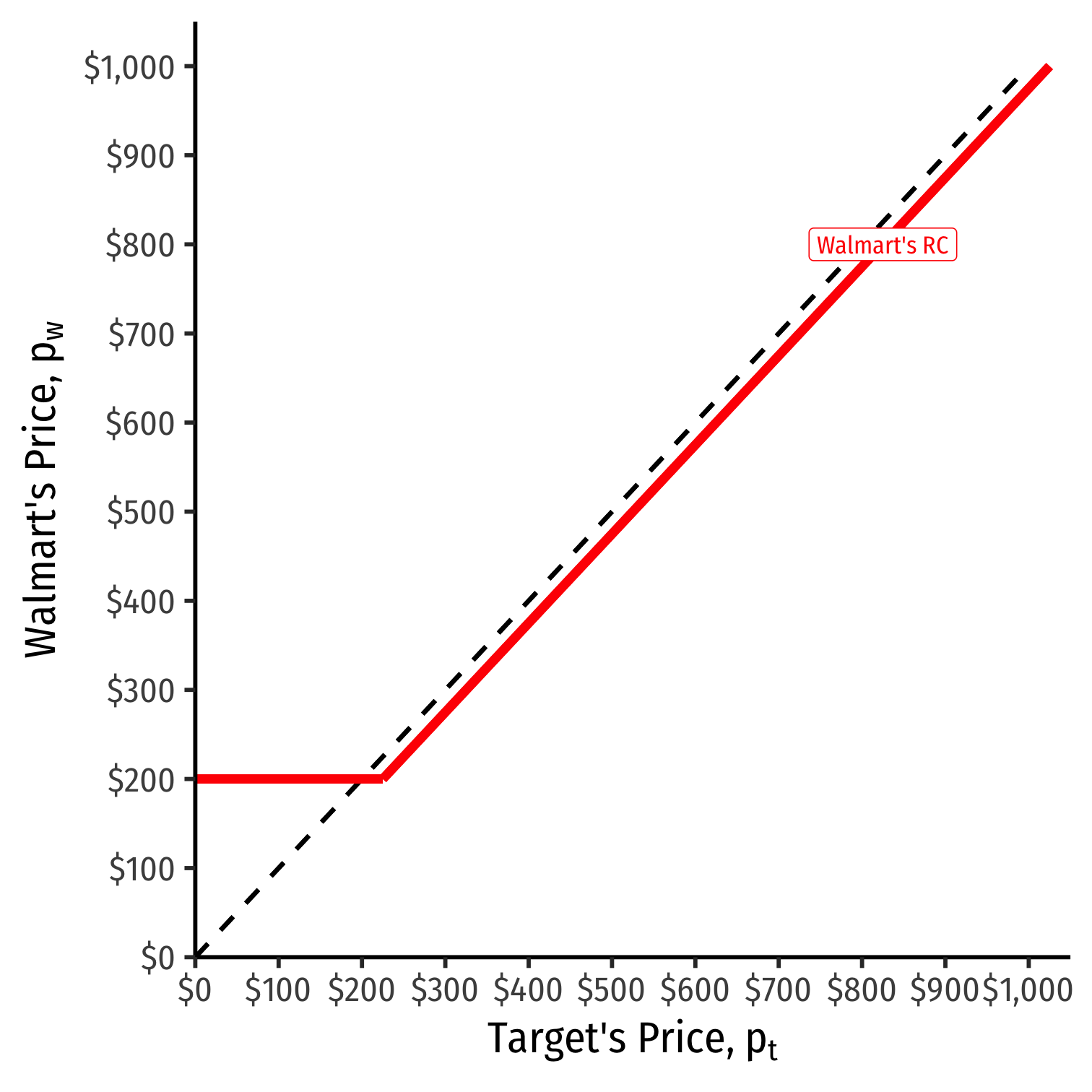
We can graph Walmart's reaction curve to Target's price
Walmart's Reaction Curve
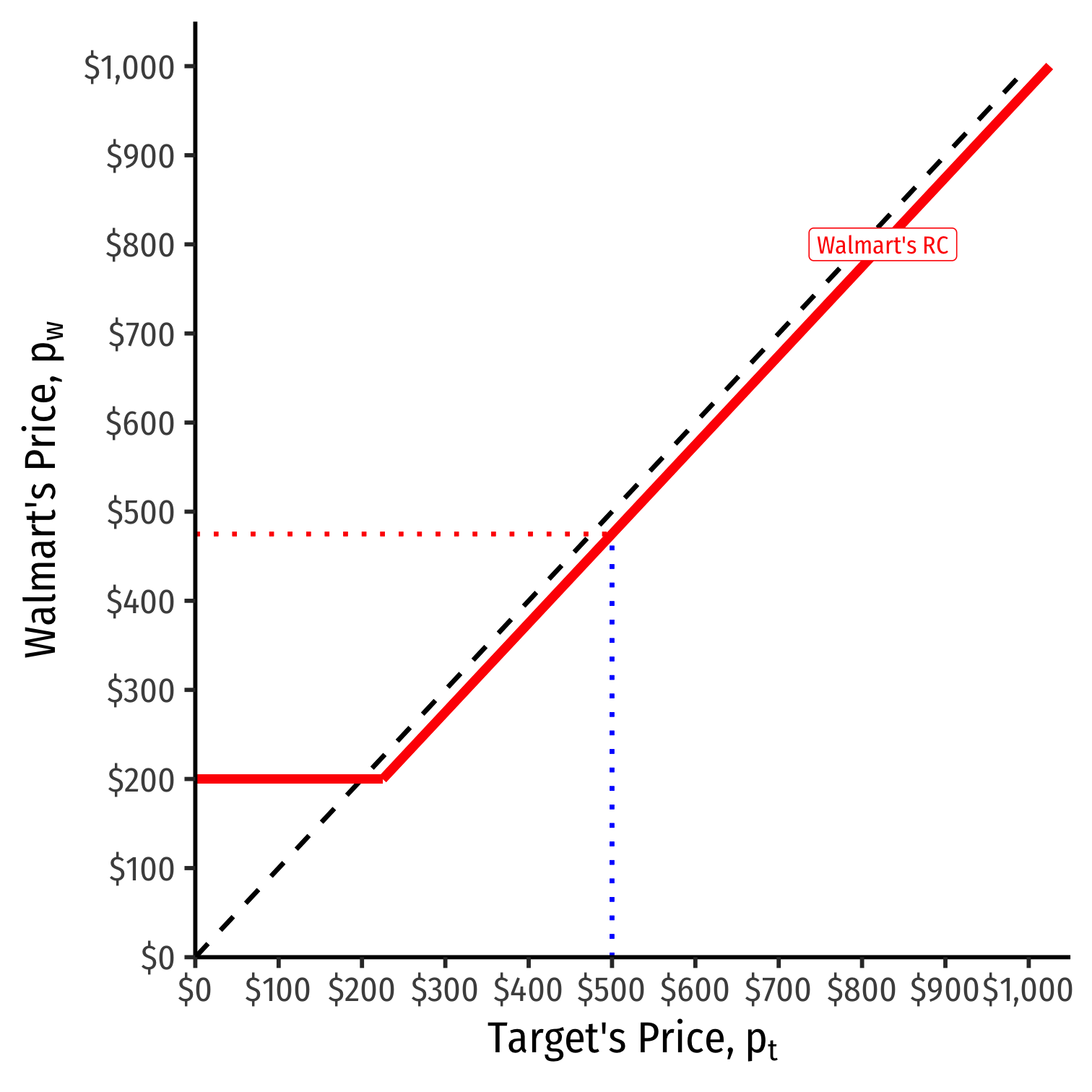
We can graph Walmart's reaction curve to Target's price
- e.g. if Target sets a price of $500, Walmart's best response is $500−ϵ
Walmart's Reaction Curve

We can graph Walmart's reaction curve to Target's price
- e.g. if Target sets a price of $500, Walmart's best response is $500−ϵ
- e.g. if Target sets a price of $300, Walmart's best response is $300−ϵ
Walmart's Reaction Curve
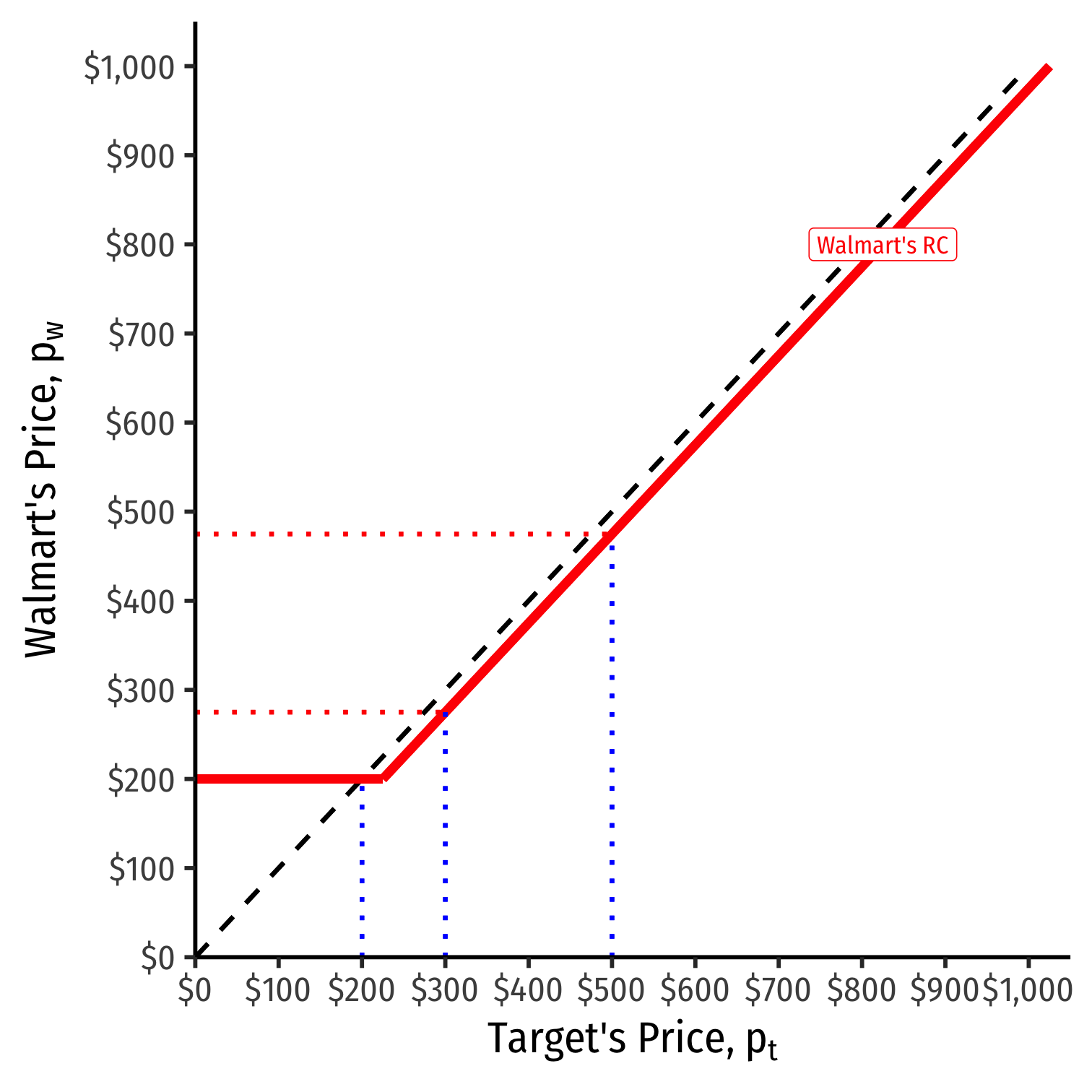
We can graph Walmart's reaction curve to Target's price
- e.g. if Target sets a price of $500, Walmart's best response is $500−ϵ
- e.g. if Target sets a price of $300, Walmart's best response is $300−ϵ
- e.g. if Target sets a price of $200, (MC) Walmart's best response is $200 (MC)
Target's Reaction Curve
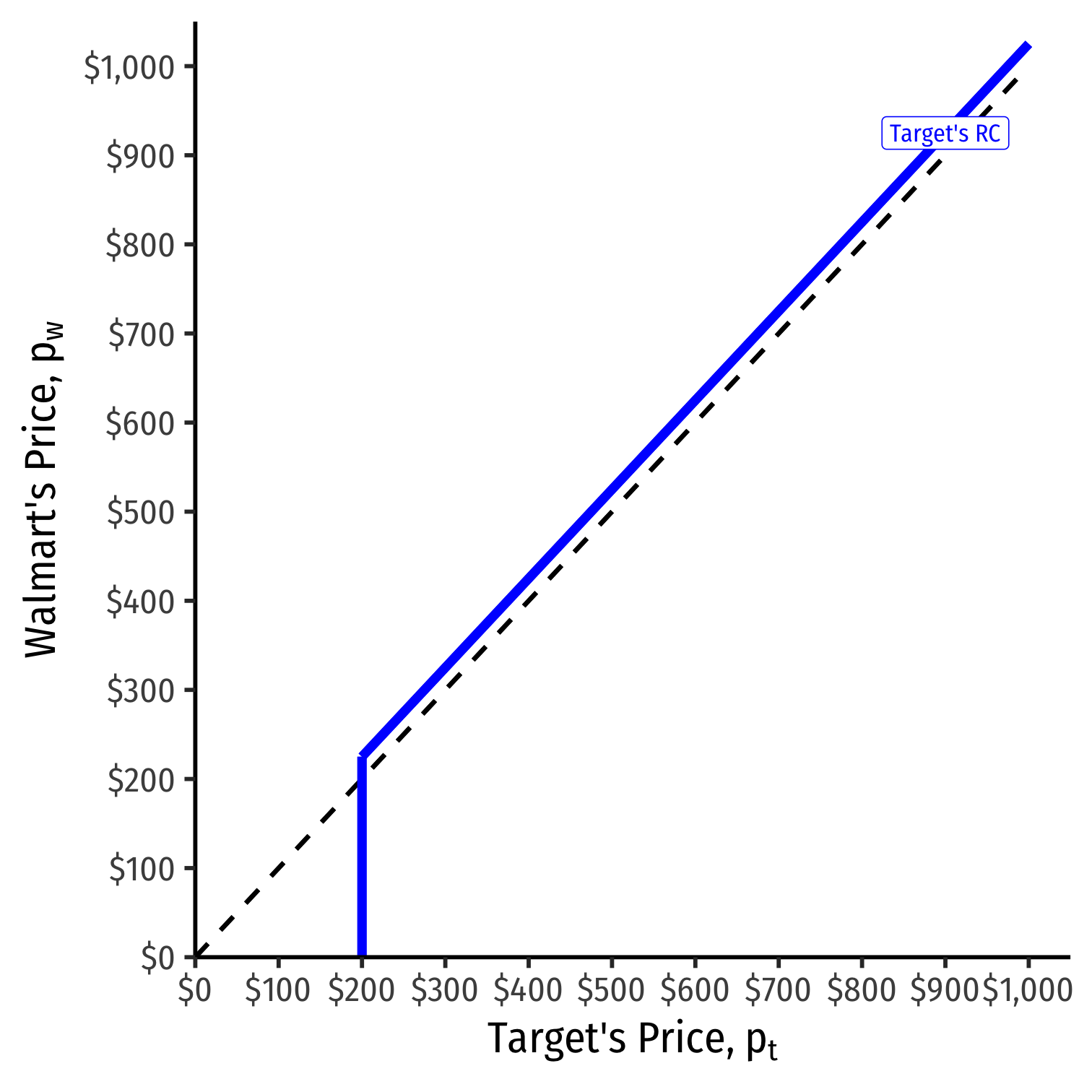
We can graph Target's reaction curve to Walmart's price
Target's Reaction Curve
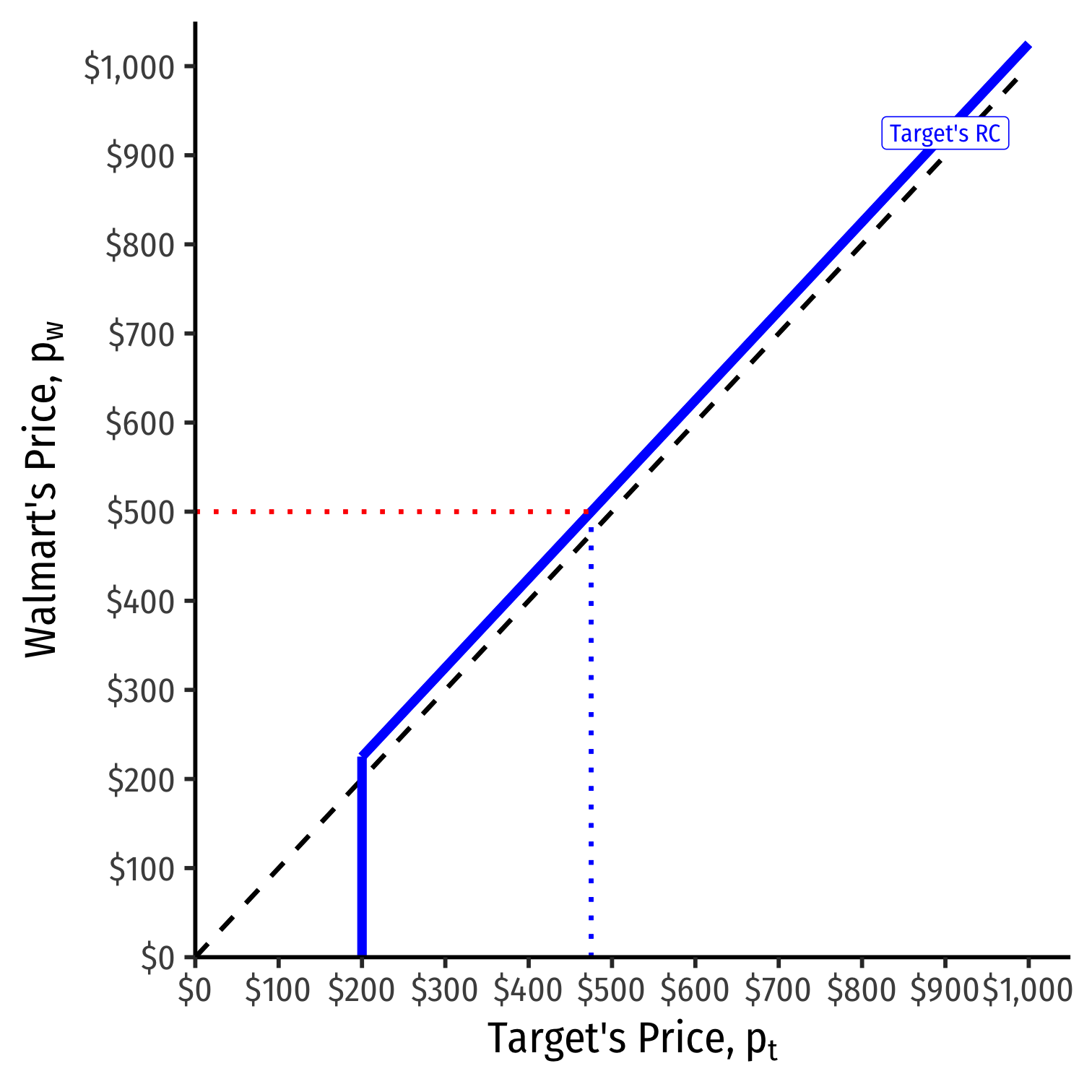
We can graph Target's reaction curve to Walmart's price
- e.g. if Walmart sets a price of $500, Target's best response is $500−ϵ
Target's Reaction Curve
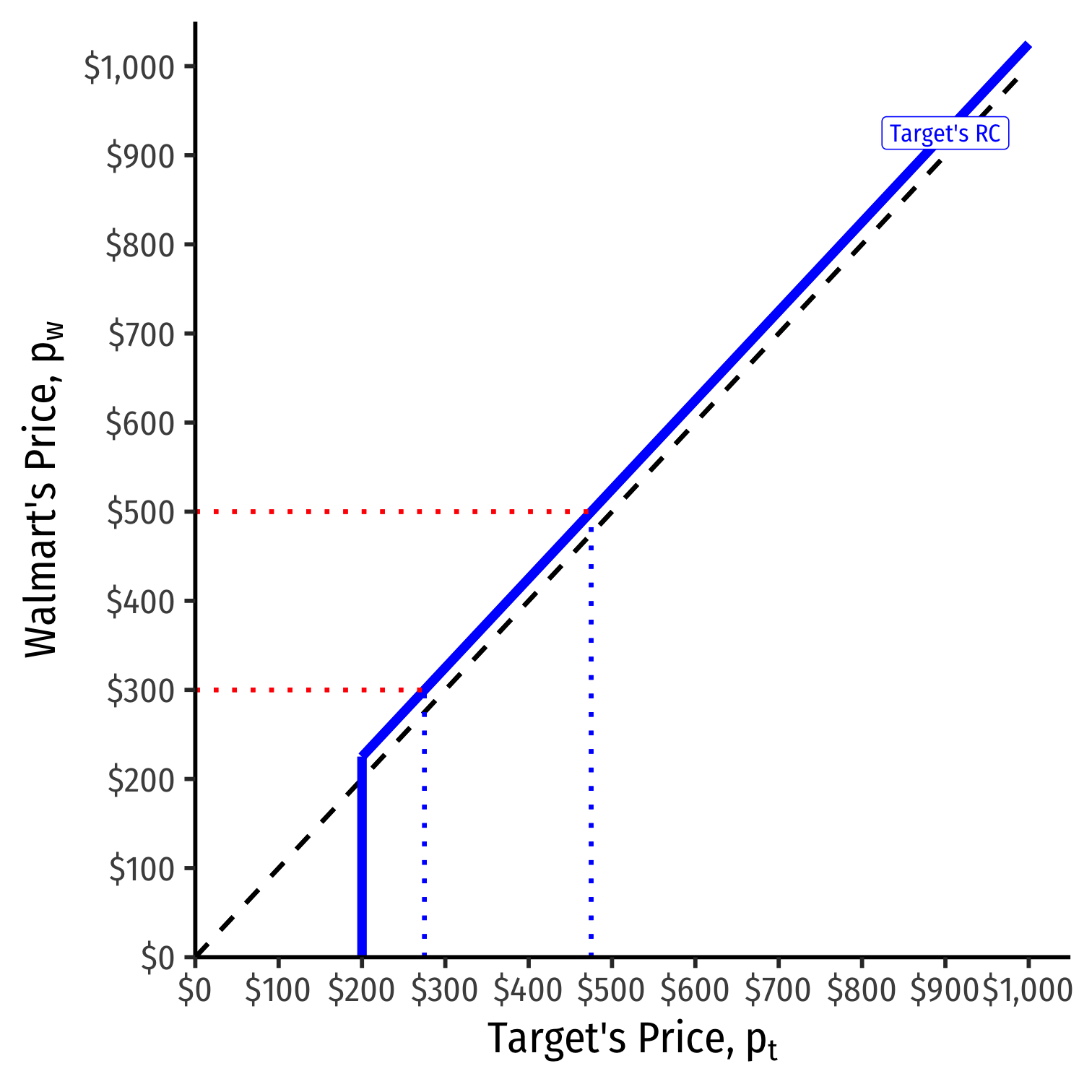
We can graph Target's reaction curve to Walmart's price
- e.g. if Walmart sets a price of $500, Target's best response is $500−ϵ
- e.g. if Walmart sets a price of $300, Target's best response is $300−ϵ
Target's Reaction Curve

We can graph Target's reaction curve to Walmart's price
- e.g. if Walmart sets a price of $500, Target's best response is $500−ϵ
- e.g. if Walmart sets a price of $300, Target's best response is $300−ϵ
- e.g. if Walmart sets a price of $200 (MC), Target's best response is $200 (MC)
Nash Equilibrium with Reaction Curves
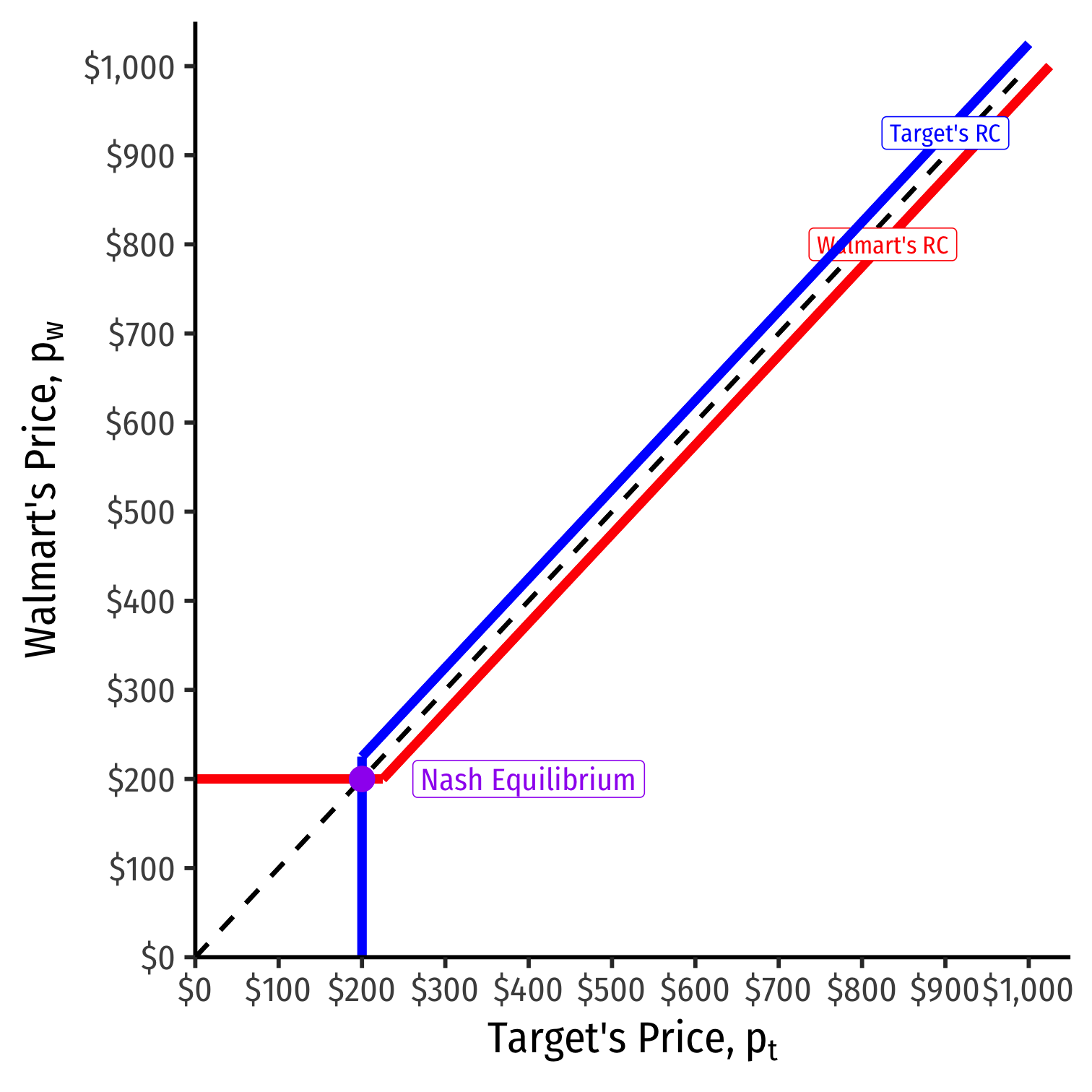
Combine both curves on the same graph
Nash Equilibrium: (pw=MC,pt=MC)
- Where both reaction curves intersect
No longer an incentive to undercut or change price