Loading [MathJax]/jax/output/HTML-CSS/jax.js
+ - 0:00:00
Notes for current slide
Notes for next slide

2.4 — Stackelberg Competition

ECON 316 • Game Theory • Fall 2021

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/gameF21
gameF21.classes.ryansafner.com

Models of Oligopoly

Three canonical models of Oligopoly

  1. Bertrand competition
    • Firms simultaneously compete on price
  2. Cournot competition
    • Firms simultaneously compete on quantity
  3. Stackelberg competition
    • Firms sequentially compete on quantity

Stackelberg Competition

Henrich von Stackelberg

1905-1946

  • "Stackelberg competition": Cournot-style competition, two (or more) firms compete on quantity to sell the same good

  • Again, firms' joint output determines the market price faced by all firms

  • But firms set their quantities sequentially

    • Leader produces first
    • Follower produces second

Stackelberg Competition: Example

Example: Return to Saudi Arabia (sa) and Iran (i), again with the market (inverse) demand curve: P=200−3QQ=qsa+qi

Stackelberg Competition: Example

Example: Return to Saudi Arabia (sa) and Iran (i), again with the market (inverse) demand curve: P=200−3QQ=qsa+qi

  • We solved for Saudi Arabia and Iran's reaction functions in Cournot competition last class: q∗sa=30−0.5qiq∗i=30−0.5qsa

Stackelberg Competition: Example

q∗sa=30−0.5qiq∗i=30−0.5qsa

  • Suppose Saudi Arabia is the Stackelberg leader and produces qsa first

Stackelberg Competition: Example

q∗sa=30−0.5qiq∗i=30−0.5qsa

  • Suppose Saudi Arabia is the Stackelberg leader and produces qsa first
  • Saudi Arabia knows exactly how Iran will respond to its output

q∗i=30−0.5qsa

Stackelberg Competition: Example

q∗sa=30−0.5qiq∗i=30−0.5qsa

  • Suppose Saudi Arabia is the Stackelberg leader and produces qsa first
  • Saudi Arabia knows exactly how Iran will respond to its output

q∗i=30−0.5qsa

  • Saudi Arabia, as leader, essentially faces entire market demand
    • But can't act like a pure monopolist!
    • knows that follower will still produce afterwards, which pushes down market price for both firms!

Stackelberg Competition: Example

  • Substitute follower's reaction function into (inverse) market demand function faced by leader

Stackelberg Competition: Example

  • Substitute follower's reaction function into (inverse) market demand function faced by leader

P=200−3qsa−3(30−0.5qsa)P=110−1.5qsa

Stackelberg Competition: Example

  • Substitute follower's reaction function into (inverse) market demand function faced by leader

P=200−3qsa−3(30−0.5qsa)P=110−1.5qsa

  • Now find MR(q) for Saudi Arabia from this by doubling the slope:

Stackelberg Competition: Example

  • Substitute follower's reaction function into (inverse) market demand function faced by leader

P=200−3qsa−3(30−0.5qsa)P=110−1.5qsa

  • Now find MR(q) for Saudi Arabia from this by doubling the slope:

MRLeader=110−3qsa

Stackelberg Competition: Example

  • Now Saudi Arabia can find its optimal quantity:

MRLeader=MC110−3qsa=2030=q∗sa

Stackelberg Competition: Example

  • Now Saudi Arabia can find its optimal quantity:

MRLeader=MC110−3qsa=2030=q∗sa

  • Iran will optimally respond by producing:

q∗i=30−0.5qsaq∗i=30−0.5(30)q∗i=15

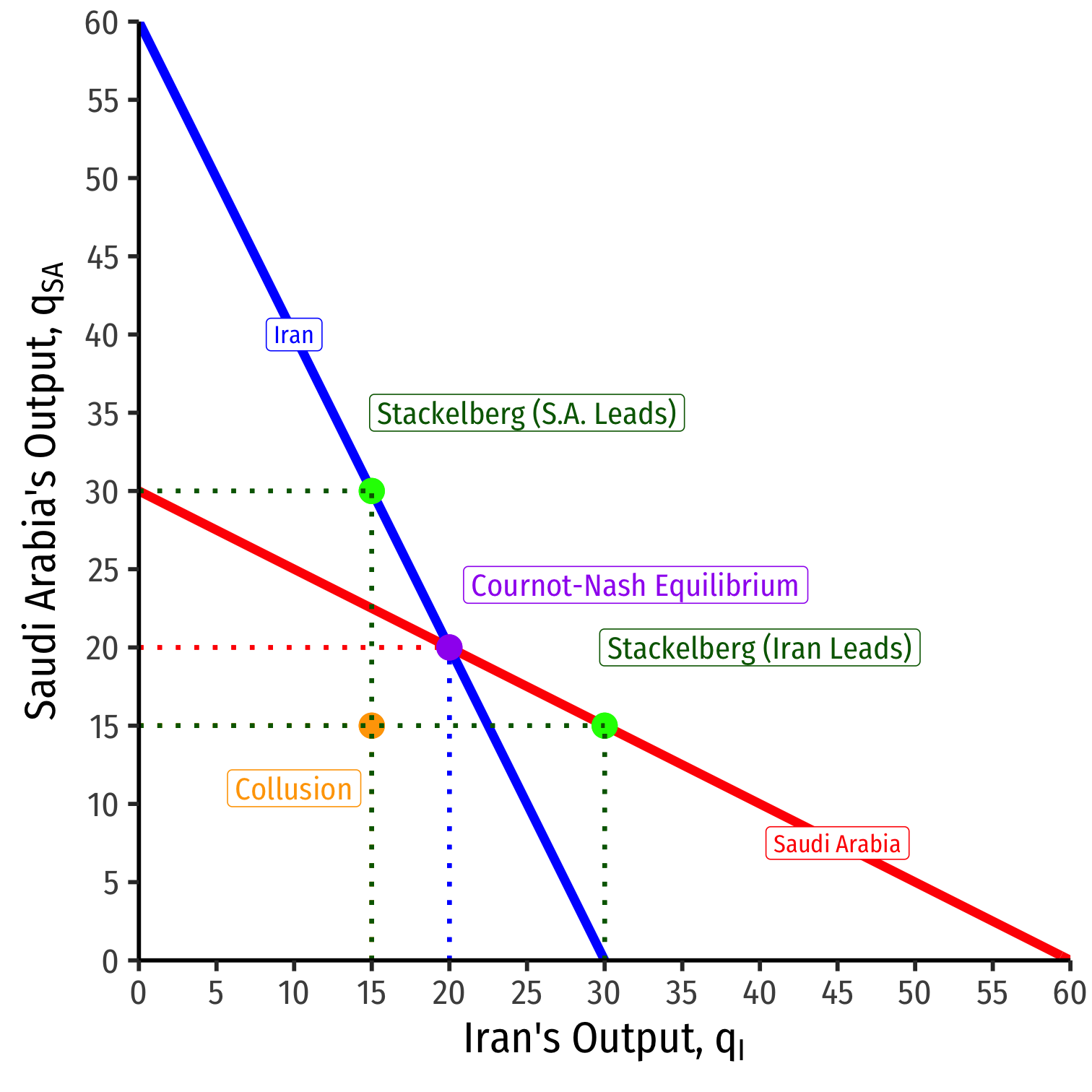
Stackelberg Equilibrium, Graphically

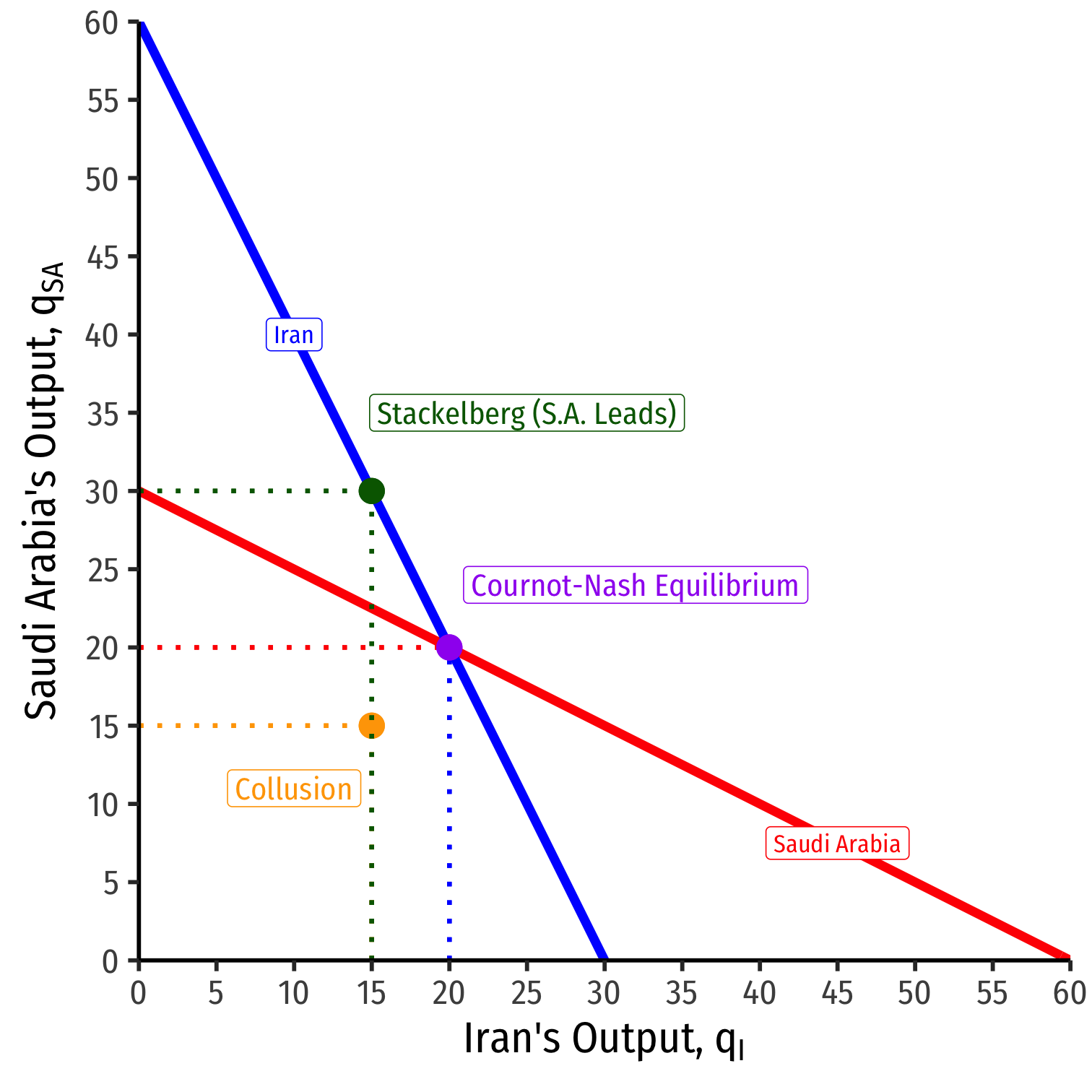
  • Stackelberg Nash Equilibrium: (q∗sa=30,q∗i=15)

Stackelberg Competition: Example

  • With q∗sa=30 and q∗i=15, this sets a market-clearing price of:

P=200−3(45)P=65

Stackelberg Competition: Example

  • With q∗sa=30 and q∗i=15, this sets a market-clearing price of:

P=200−3(45)P=65

  • Saudi Arabia's profit would be:

πsa=30(65−20)πsa=$1,350

Stackelberg Competition: Example

  • With q∗sa=30 and q∗i=15, this sets a market-clearing price of:

P=200−3(45)P=65

  • Saudi Arabia's profit would be:

πsa=30(65−20)πsa=$1,350

  • Iran's profit would be:

πi=15(65−20)πi=$675

Stackelberg Equilibrium, The Market

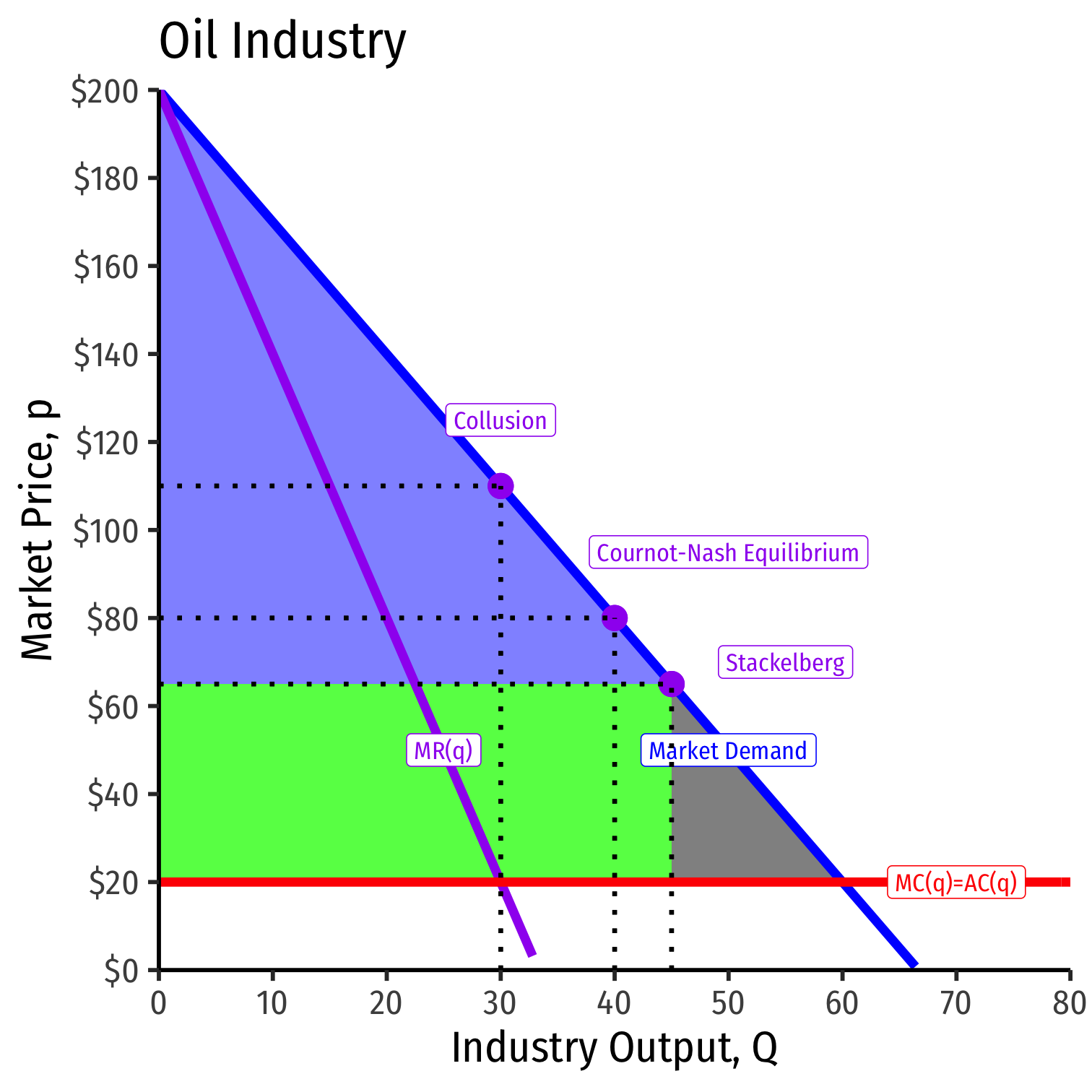
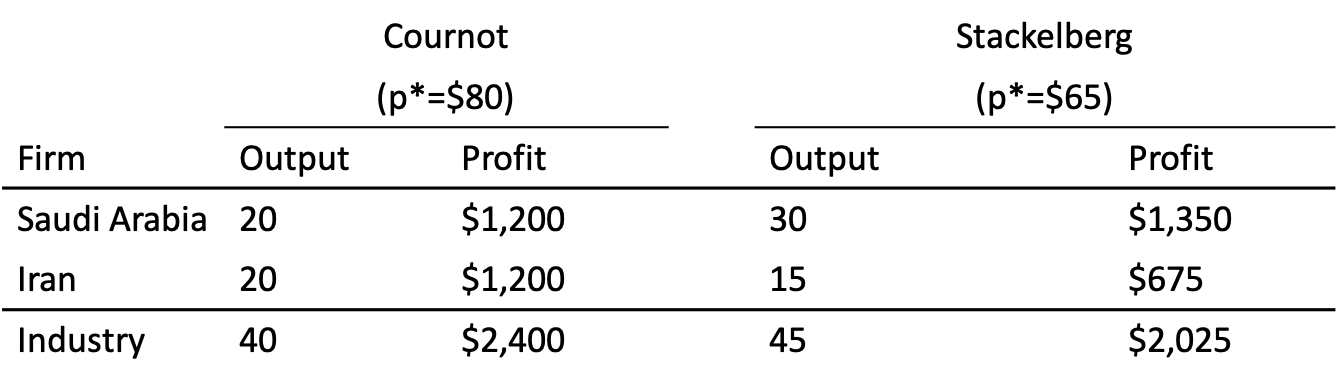
Cournot vs. Stackelberg Competition

  • Leader Saudi Arabia ↑ its output and ↑ profits

  • Follower Iran forced to ↓ its output and accept ↓ profits

Stackelberg and First-Mover Advantage

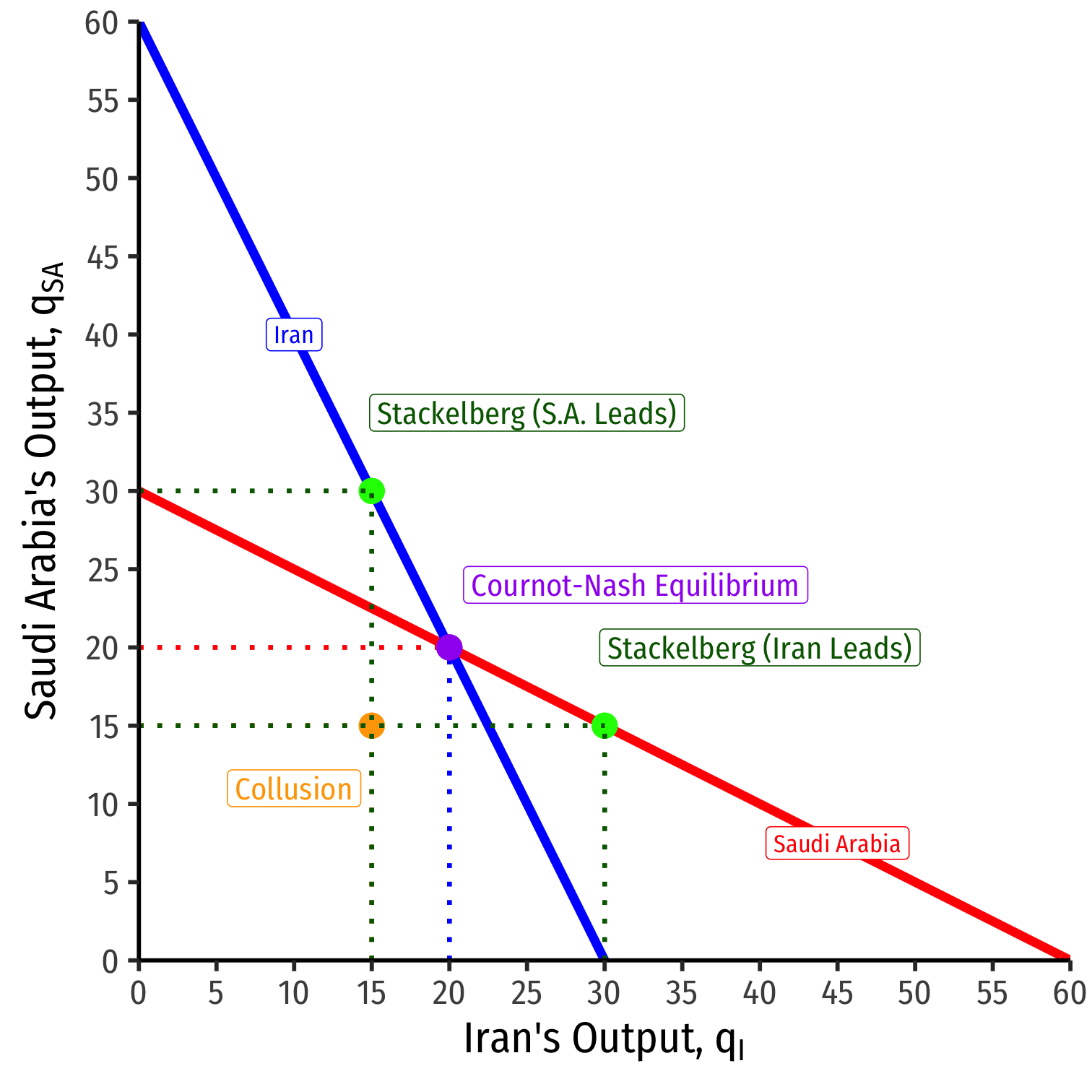
  • Stackelberg leader clearly has a first-mover advantage over the follower

    • Leader: q∗=30, π=1,350
    • Follower: q∗=15, π=675

  • If firms compete simultaneously (Cournot): q∗=20, π=1,200 each

  • Leading ≻ simultaneous ≻ Following

Stackelberg and First-Mover Advantage

  • Stackelberg Nash equilibrium requires perfect information for both leader and follower

    • Follower must be able to observe leader's output to choose its own
    • Leader must believe follower will see leader's output and react optimally

  • Imperfect information reduces the game to (simultaneous) Cournot competition

Stackelberg and First-Mover Advantage

  • Again, leader cannot act like a monopolist

    • A strategic game! Market output (that pushes down market price) is Q=qsa+qi

  • Leader's choice of 30 is optimal only if follower responds with 15

Comparing All Oligopoly Models

  • Output: Qm<Qc<Qs<Qb
  • Market price: Pb<Ps<Pc<Pm
  • Profit: πb=0<πs<πc<πm

Where subscript m is monopoly (collusion), c is Cournot, s is Stackelberg, b is Bertrand

Stackelberg Competition: Moblab

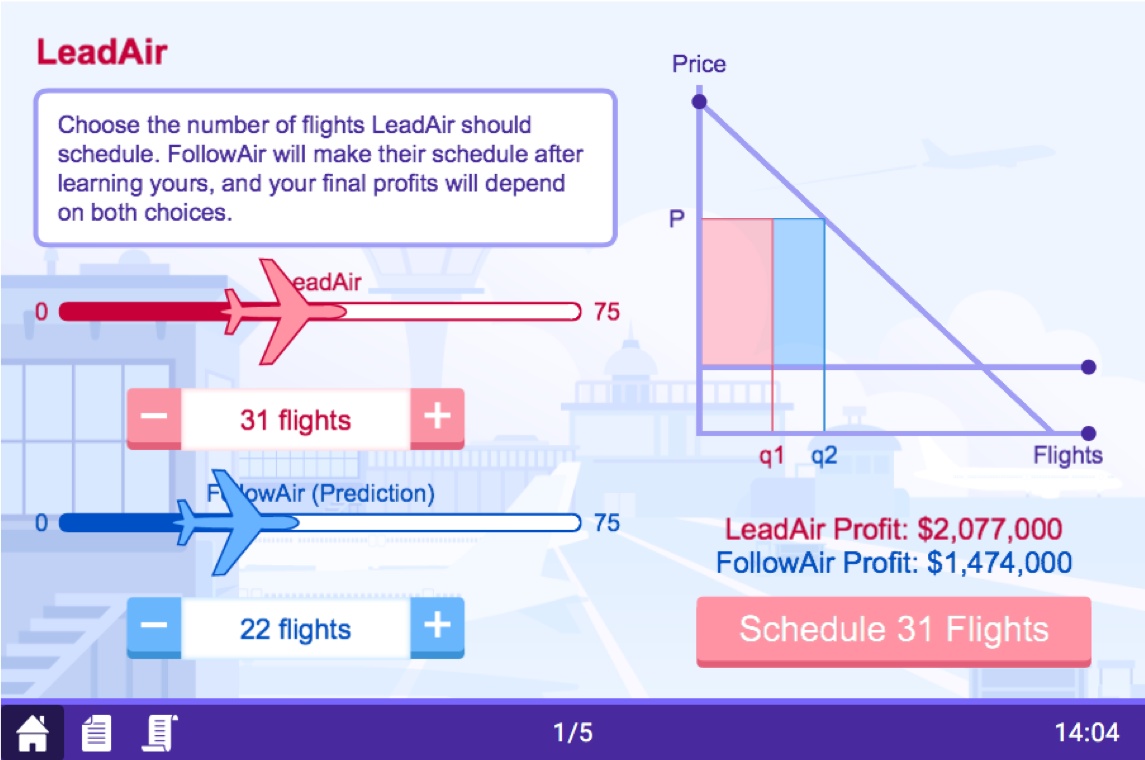
Stackelberg Competition: Moblab

  • Each of you is one Airline competing against another in a duopoly

    • Each pays same per-flight cost
    • Market price determined by total number of flights in market

  • LeadAir first chooses its number of flights, publicly announced

  • FollowAir then chooses its number of flights

Models of Oligopoly

Three canonical models of Oligopoly

  1. Bertrand competition
    • Firms simultaneously compete on price
  2. Cournot competition
    • Firms simultaneously compete on quantity
  3. Stackelberg competition
    • Firms sequentially compete on quantity

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
oTile View: Overview of Slides
Esc Back to slideshow