2.5 — Contestable Markets

# 2.5 — Contestable Markets
## ECON 316 • Game Theory • Fall 2021
### Ryan Safner Assistant Professor of Economics <a href="mailto:safner@hood.edu">safner@hood.edu</a> <a href="https://github.com/ryansafner/gameF21">ryansafner/gameF21</a> <a href="https://gameF21.classes.ryansafner.com"> gameF21.classes.ryansafner.com</a>

---

# Outline

### [Contestable Markets](#3)
### [Scenario I: Identical Costs](#8)
### [Scenario II: Entrant has Higher Costs](#12)
### [Scenario III: Fixed Costs](#15)
### [Scenario IV: Sunk Costs](#18)
### [Implications for Markets and Policy](#24)

---

# Contestable Markets

---

# Is Monopoly a Nash Equilibrium?

- Now that we understand Nash equilibrium and the economics of oligopoly...

- Are outcomes of *other* market structures Nash equilibria?

]

![:scale 75%](../images/entry.jpg)
]
]

---

# Is Monopoly a Nash Equilibrium?

- Now that we understand Nash equilibrium and the economics of oligopoly...

- Are outcomes of *other* market structures Nash equilibria?

- **Perfect competition**: no firm wants to raise or lower price given the market price `$\checkmark$`

]

![:scale 75%](../images/entry.jpg)
]
]

---

# Is Monopoly a Nash Equilibrium?

- **Monopolist** maximizes `$\pi$` by setting `$q^*$`: `$MR=MC$` and `$p^*=Demand(q^*)$`

- This is *an* equilibrium, but is it the *only* equilibrium?

- We've assumed just a *single* player in the model

- .hi-purple[What about *potential* competition?]

]

![:scale 75%](../images/entry.jpg)
]
]

---

# An Entry Game

- Model the market as an .hi-purple[entry game], with two players:

1. .hi-red[**Incumbent**] which sets its price `$\color{red}{p_I}$`

2. .hi-blue[**Entrant**] decides to **stay out** or **enter** the market, setting its price `$\color{blue}{p_E}$`

- Bertrand (price) competition between 2 firms with similar products `$\implies$` .hi-purple[consumers buy only from firm with lower price]

]

![:scale 75%](../images/entry.jpg)
]
]

---

# Scenario I: Identical Costs

---

# Contestable Markets II

.pull-left[
.smallest[
- Suppose both firms have identical costs: 
`$$\begin{align*}
C(q)&=cq\\
MC(q)&=c\\ \end{align*}$$`

- If .hi-red[Incumbent] sets `$\color{red}{p_I}>c$`
 - .hi-blue[Entrant] would enter and set `$\color{blue}{p_E}=\color{red}{p_I}-\epsilon$`.magenta[†]
]

]

---

# Contestable Markets II

.pull-left[
.smallest[
- Suppose both firms have identical costs: 
`$$\begin{align*}
C(q)&=cq\\
MC(q)&=c\\ \end{align*}$$`

- If .hi-red[Incumbent] sets `$\color{red}{p_I}>c$`
 - .hi-blue[Entrant] would enter and set `$\color{blue}{p_E}=\color{red}{p_I}-\epsilon$`.magenta[†]
 - .hi-red[Incumbent] foresees this possibility, and wants to lower its price `$\color{red}{p_I}<\color{blue}{p_E}$`
 - This potential undercutting would continue logically until...

]

---

# Contestable Markets II

.pull-left[
.smaller[
- .hi-purple[Nash Equilibrium]: `$\big(\color{red}{p_I}=c$`, .blue[Stay Out] `$\big)$`

- .hi-purple[A market with a single firm, but the **competitive outcome**!]
  - `$p^*=MC$`, `$\color{green}{\pi=0}$`
  - competitive `$q^*$`
  - max .hi-blue[Consumer Surplus], no DWL
]
]

<img src="2.5-slides_files/figure-html/unnamed-chunk-1-1.png" width="504" style="display: block; margin: auto;" />
]

---

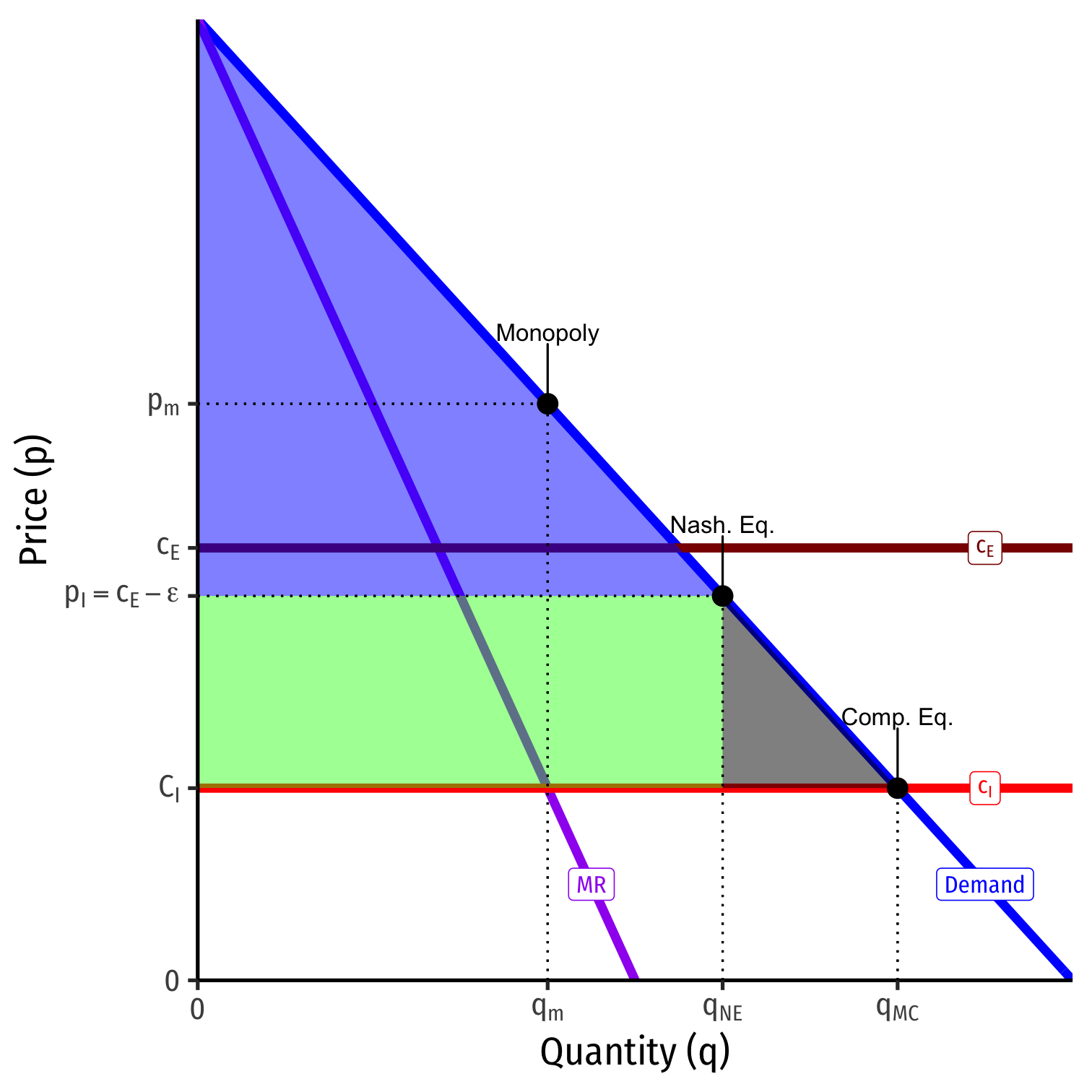
# Scenario II: Entrant has Higher Costs

---

# Contestable Markets II

.smaller[
- What if the .hi-blue[Entrant] has *higher costs* than the .hi-red[Incumbent]: `$\color{blue}{c_E}>\color{red}{c_I}$`?
]
]

---

# Contestable Markets II

.smaller[
- What if the .hi-blue[Entrant] has *higher costs* than the .hi-red[Incumbent]: `$\color{blue}{c_E}>\color{red}{c_I}$`?

- .hi-purple[Nash equilibrium]: 
`$\big(\color{red}{p_I}=\color{blue}{p_E-\epsilon}$`, .blue[Stay Out] `$\big)$`

- One firm again, with some inefficiency
  - But not as bad as monopoly!
]
]

<img src="2.5-slides_files/figure-html/unnamed-chunk-2-1.png" width="504" style="display: block; margin: auto;" />
]

---

# Scenario III: Fixed Costs

---

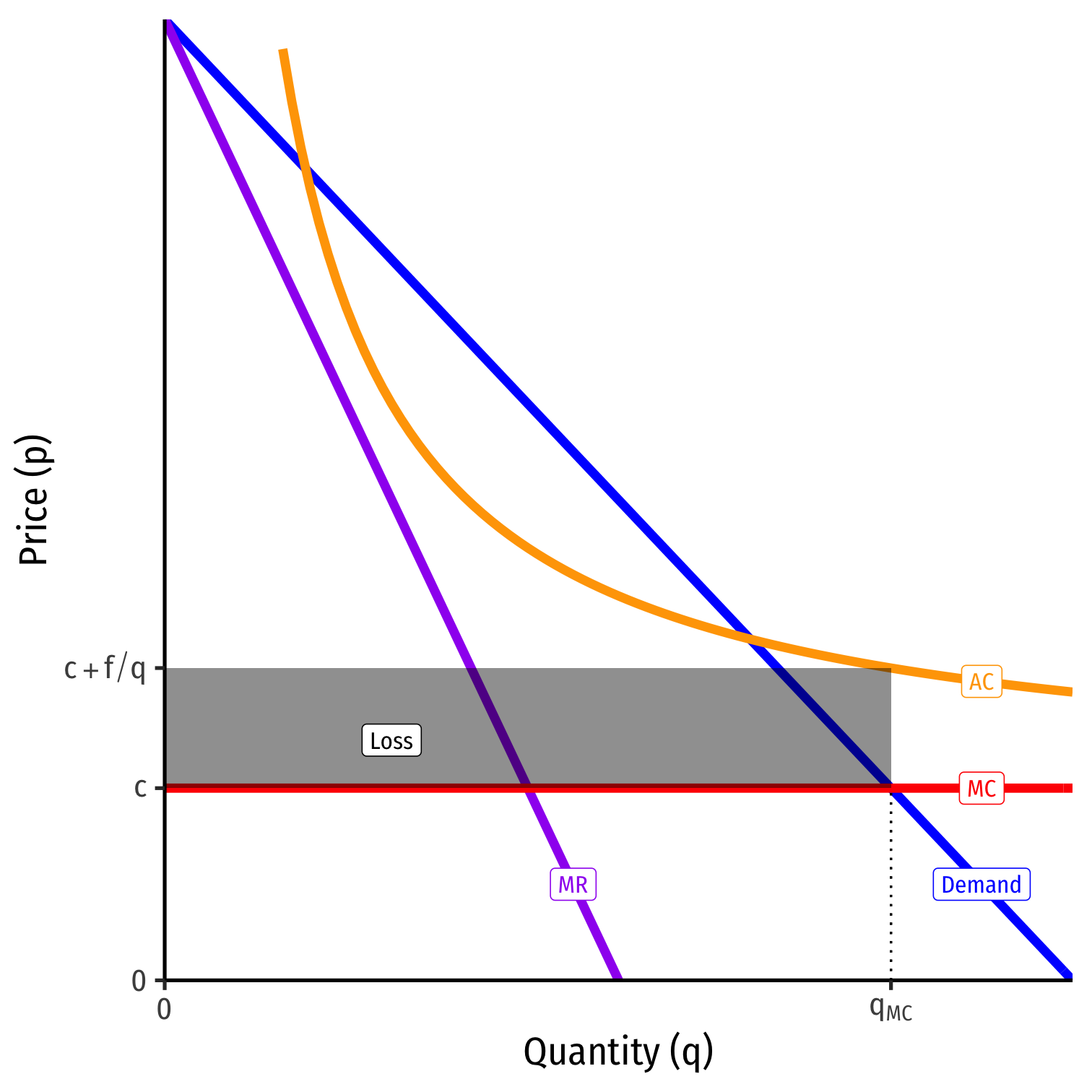
# Contestable Markets III

- What if there are **fixed costs**, `$f$`?

`$$\begin{align*}
C(q)&=cq+f \\
MC(q)&=c \\
AC(q)&=c+\frac{f}{q} \\
\end{align*}$$`

- With high enough `$f$`, .hi[economies of scale] prevent marginal cost pricing from a being profitable Nash Equilibrium

`$$\pi_{p=MC}=-\frac{f}{q}<0$$`

]

<img src="2.5-slides_files/figure-html/unnamed-chunk-3-1.png" width="504" style="display: block; margin: auto;" />
]

---

# Contestable Markets IV

- Again, only a single firm with some inefficiency
  - But not as bad as monopoly!
  - .red[Incumbent] earns no profits!

]
]
.pull-right[

<img src="2.5-slides_files/figure-html/unnamed-chunk-4-1.png" width="504" style="display: block; margin: auto;" />
]

---

# Scenario IV: Sunk Costs

---

# What About *Sunk* Costs? I

- If firm exits, could sell these assets (e.g. machines, real estate) to recover costs
  - Thus, .hi-purple[“hit-and-run” competition] remains potentially profitable
  - Maintains .hi-purple[credible threat] against incumbent acting as a monopolist

]

---

# What About *Sunk* Costs? I

- But what if assets are *not* sellable and costs *not* recoverable - i.e. .hi[sunk costs]?

- e.g. research and development, spending to build brand equity, advertising, worker-training for industry-specific skills, etc

]

---

# What About *Sunk* Costs? II

- But are *new* costs and risk to .hi-blue[Entrant], lowering expected profits

- In effect, sunk costs raise `$\color{blue}{c_E}>\color{red}{c_I}$`, and return us back to our Scenario II

- .hi[Nash equilibrium]: .hi-red[Incumbent] deters entry with `$\color{red}{p_I}=\color{blue}{p_E}-\epsilon$`
  - Inefficient, `$p>AC$`, but again not monopoly

]

---

# Contestable Markets: Recap

.pull-left[
- .hi-purple[Markets are **contestable** if]:
  1. There are no barriers to entry or exit
  2. Firms have similar technologies (i.e. similar cost structure)
  3. There are no sunk costs
  
- Economies of scale need not be inconsistent with competitive markets (as is assumed) if they are contestable

- Generalizes “perfect competition” model in more realistic way, also game-theoretic
]

---

# Contestable Markets: Summary

William Baumol

(1922--2017)

]
]

> "This means that...an incumbent, even if he can threaten retaliation after entry, dare not offer profit-making opportunities to potential entrants because an entering firm can hit and run, gathering in the available profits and departing when the going gets rough."

]

.source[Baumol, William, J, 1982, "Contestable Markets: An Uprising in the Theory of Industry Structure," *American Economic Review,* 72(1): 1-15]

---

# Implications for Markets and Policy

---

# Implications for Competition

- Regulation & antitrust (once) focus(ed) on *number* of firms
    - "Count the number of firms, if it's 1, it's a monopoly!"

- .hi-turquoise[Perfect competition as “gold standard”, only market arrangement that is socially efficient]:
  - .hi-purple[Allocatively efficient]: `$p=MC$`, `$DWL=0$`
  - .hi-purple[Productively efficient]: `$p=AC_{min}$`
]

---

# Implications for Competition

- But number of firms is **endogenous** and **can evolve over time**!
  - Function of how firms mutually interact strategically

- A more **dynamic** situation: firms respond over time

]

---

# Implications for Competition

- Perfect competition **not** the *only* socially efficient market-structure
  - Market with number of firms (even 1) may be efficient .hi[if it is contestable]

- .hi-purple[Regulation and antitrust should consider whether a market is *contestable*, not just the *number* of firms]
  - Free entry
  - No sunk costs
]

---
# Implications for Competition

.pull-right[
.smaller[
- Firms engaging in egregious monopolistic behavior `$(\downarrow q$`, `$\uparrow p>MC$`, `$\pi>0$`) largely persist because of .hi-purple[barriers to entry]
  - Attempts to make market **uncontestable**

- Business activities or political dealings with the goal to raise `$\color{blue}{c_E}>\color{red}{c_I}$`
  - Lower your own costs, or raise your rivals'!
  - (Recall Cournot competition with different costs)
]
]

---

# Monopoly Or Contestable Market?

---

# Contestable Markets

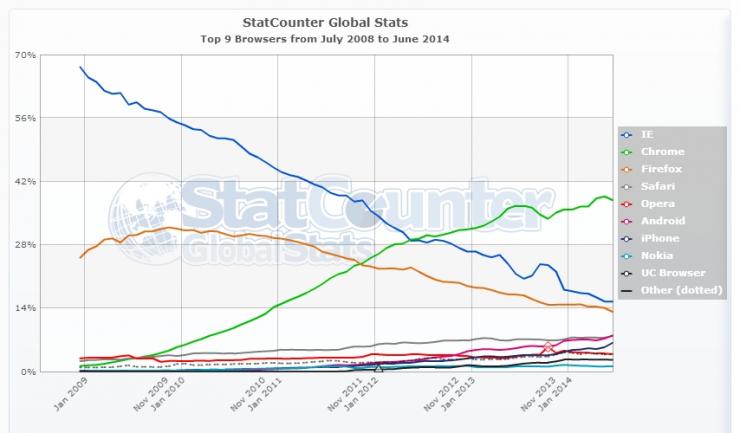
> "Of far greater concern to Microsoft is the competition from new and emerging technologies, some of which are currently visible and others of which certainly are not. This array of known, emerging, and wholly unknown competitors places enormous pressure on Microsoft to price competitively and innovate aggressively." (Schmalensee 1999)

]

---

# Contestable Markets

---

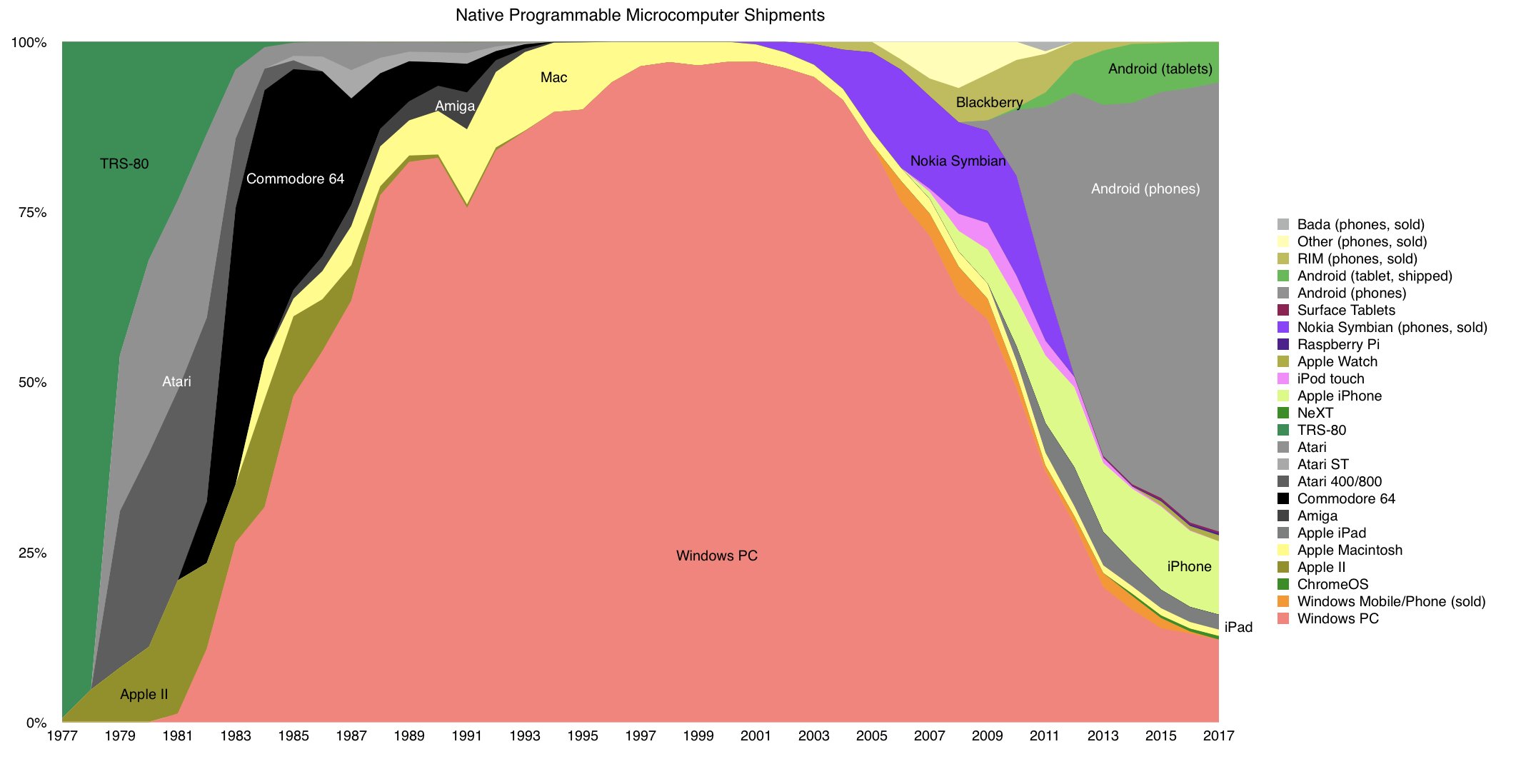
# Contestable Markets