+ - 0:00:00
Notes for current slide
Notes for next slide

3.1 — Mixed Strategies

ECON 316 • Game Theory • Fall 2021

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/gameF21
gameF21.classes.ryansafner.com

Outline

When Pure Strategies Won't Work

MSNE in Constant Sum Games

Coordination Games: PSNE and MSNE

When Pure Strategies Won't Work

When Pure Strategies Won't Work

When Pure Strategies Won't Work

Oskar Morgenstern

1902—1977

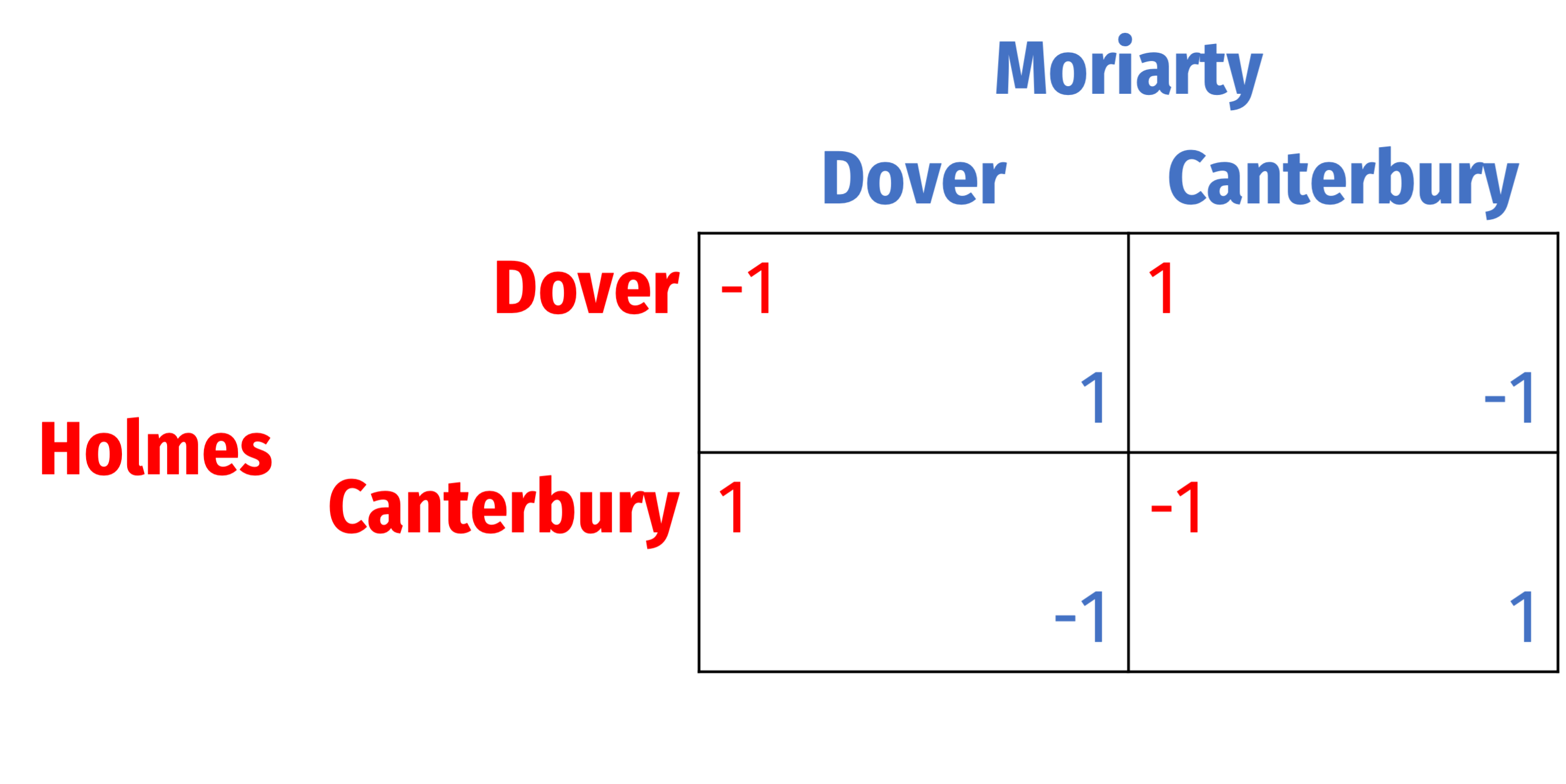
“Sherlock Holmes, pursued by his opponent, Moriarty, leaves London for Dover. The train stops at a station on the way, and he alights there rather than travelling on to Dover. He has seen Moriarty at the railway station, recognizes that he is very clever and expects that Moriarty will take a faster special train in order to catch him in Dover. Holmes’s anticipation turns out to be correct. But what if Moriarty had been still more clever, had estimated Holmes’s mental abilities better and had foreseen his actions accordingly? Then, obviously, he would have travelled to the intermediate station [Canterbury]. Holmes again would have had to calculate that, and he himself would have decided to go on to Dover. Whereupon, Moriarty would again have ‘reacted’ differently,” (p.173-4).

Morgenstern, Oskar, 1935, “Perfect Foresight and Economic Equilibrium,”

When Pure Strategies Won't Work

“‘All that I have to say has already crossed your mind,’ said he. ‘Then possibly my answer has crossed yours,’ I replied. ‘You stand fast?’ ‘Absolutely.’”

— Arthur Conan Doyle, 1893, The Final Problem

When Pure Strategies Won't Work

When Pure Strategies Won't Work

Expected Value

  • Expected value of a random variable X, written E(X) (and sometimes μ), is the long-run average value of X "expected" after many repetitions

E(X)=k∑i=1pixi

Expected Value

  • Expected value of a random variable X, written E(X) (and sometimes μ), is the long-run average value of X "expected" after many repetitions

E(X)=k∑i=1pixi

  • E(X)=p1x1+p2x2+⋯+pkxk

  • A probability-weighted average of X, with each possible X value, xi, weighted by its associated probability pi

  • Also called the "mean" or "expectation" of X, always denoted either E(X) or μX

Expected Value: Example I

Example: Suppose you lend your friend $100 at 10% interest. If the loan is repaid, you receive $110. You estimate that your friend is 99% likely to repay, but there is a default risk of 1% where you get nothing. What is the expected value of repayment?

Mixed Strategies

  • Pure strategy: is a complete strategy profile that a player will play

    • Recall, strategy is a list of choices player will take at every possible decision node

  • Mixed strategy is a probability distribution over a strategy profile

    • Plays a variety of pure strategies according to probabilities

Mixed Strategies

  • The logic of mixed strategies is best understood in the context of repeated constant-sum games

  • If you play one strategy repeatedly (i.e. a pure strategy), your opponent can exploit your (predictable) strategy with their best response

  • You want to “keep your opponent guessing”

Mixed Strategy Nash Equilibrium

  • We have already seen Nash equilibrium in pure strategies (PSNE)

  • Nash (1950) proved that any n-player game with a finite number of pure strategies has at least one equilibrium

    • A game may have no PSNE, but there will always be a unique mixed strategy Nash equilibrium (MSNE)
    • Games may have both pure and a mixed NE

Mixed Strategy Nash Equilibrium

  • Finding this is relatively straightforward with two players and two strategies
  1. Let p be the probability of one player playing one of their available strategies
    • Let (1-p) be the probability of that player playing their other available strategy
  2. Let q be the probability of the other player playing one of their available strategies
    • Let (1-q) be the probability of that player playing their other available strategy
  • There exists some (p,q) mix that is a Nash equilibrium in mixed strategies

MSNE in Constant Sum Games

MSNE in Constant Sum Games

  • Consider the following game between a Kicker and a Goalie during a penalty kick

MSNE in Constant Sum Games

  • Consider the following game between a Kicker and a Goalie during a penalty kick

  • A constant sum game (in this case, zero-sum)

    • If both choose same direction, Goalie blocks goal
    • If both choose different directions, Kicker gets goal

MSNE in Constant Sum Games

  • Palacios-Huerta (2003) calculated average success rates in English, Spanish, & Italian leagues (1995-2000)

  • If both Kicker and Goalie choose same direction, Kicker's payoff is higher if he chooses his natural side (often Right)

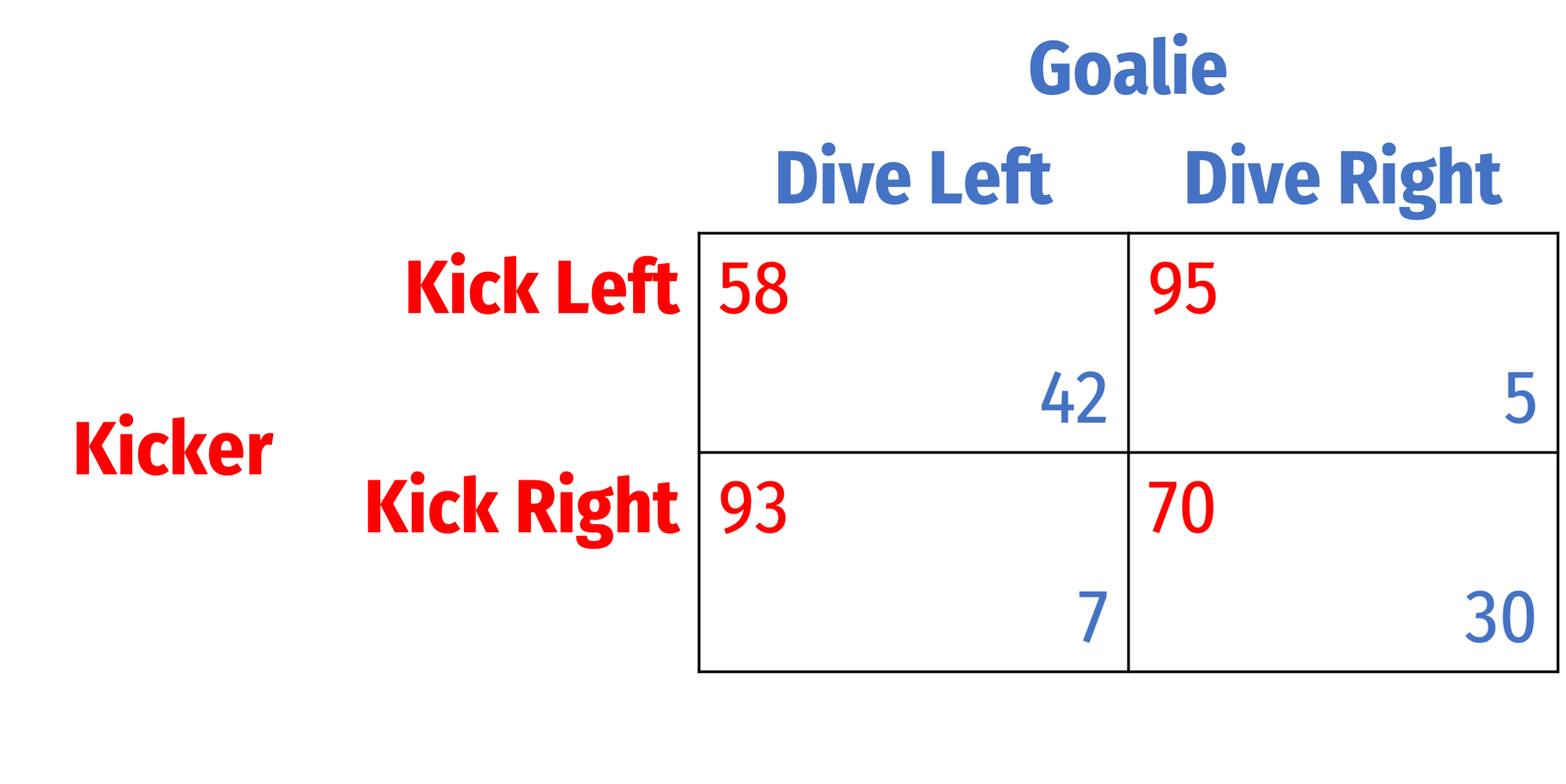
Palacios-Huerta, Ignacio, 2003, “Professionals Play Minimax,” Review of Economic Studies 70(2): 395–415

MSNE in Constant Sum Games

  • This game has no Nash equilibrium in pure strategies (PSNE)
    • From any outcome, at least one player would prefer to switch strategies
    • No outcome has all players playing a best response

MSNE in Constant Sum Games

  • What if Kicker were to randomize strategies

    • Say 50% of the time, Kick Left, 50% of the time, Kick Right

  • Let p be probability that Kicker plays Kick Left

    • p=0.50

MSNE in Constant Sum Games

  • Then Goalie wants to maximize his expected payoff, given Kicker plays Kick Left with p=0.50

MSNE in Constant Sum Games

  • Then Goalie wants to maximize his expected payoff, given Kicker plays Kick Left with p=0.50

  • If Goalie plays Dive Left: E[Dive Left]=42(p)+7(1−p)=42(0.50)+7(1−0.50)

    • He can expect to earn 24.5

MSNE in Constant Sum Games

  • Then Goalie wants to maximize his expected payoff, given Kicker plays Kick Left with p=0.50

  • If Goalie plays Dive Right: E[Dive Right]=5(p)+30(1−p)=5(0.50)+30(1−0.50)

    • He can expect to earn 17.5

MSNE in Constant Sum Games

  • Then Goalie wants to maximize his expected payoff, given Kicker plays Kick Left with p=0.50

  • Goalie will play Dive Left to maximize his expected payoff (24.5 ≻ 17.5)

MSNE in Constant Sum Games

  • Now consider Kicker's expected payoff under this mixed strategy

  • Since Goalie will Dive Left to maximize his expected payoff, Kicker can expect to earn:

58(p)+93(1−p)58(0.50)+93(1−0.50)75.5

  • Goalie playing Dive Left holds Kicker's expected payoff down to 75.5

The Minimax Theorem

  • In constant sum games, note that even in mixed strategies, one player increases their own (expected) payoff by pulling down the other player's (expected) payoff!

  • In this game, even expected payoffs always sum to 100

    • Kicker's E[π]=75.5
    • Goalie's E[π]=24.5

The Minimax Theorem

  • von Neumann & Morgenstern’s minimax theorem (simplified): in a 2-person, constant sum game, each player maximizes their own expected payoff by minimizing their opponent's expected payoff

  • The name “minimax” is a popular strategy in games, trying to minimize the risk of your maximum possible loss

Penalty Kicks: 50:50?

  • Kicker's “randomizing” 50:50 (Kick Left, Kick Right) was not random enough!

  • Goalie recognizing this pattern can exploit it and hold down Kicker's expected payoff

  • Kicker can do better by picking a better p (and similarly, so can Goalie)

    • Hint: if Goalie knew Kicker's p before Goalie chose, would he have a clearly better choice of Dive Left vs. Dive Right?

The Opponent Indifference Principle

  • Want to find the optimal probability mix that leaves your opponent(s) indifferent between their strategies to respond

  • In constant sum games (i.e. sports, board games, etc)

    • Making your opponent indifferent ⟹ minimizing your opponent's ability to recognize & exploit patterns in your actions

  • This principle is the same in non-constant sum games too!

  • Implies game is played repeatedly

  • Not always intuitive, but a simple principle

Kicker's Optimal Choice of p

  • We want to find Kicker's optimal mixed strategy that leaves Goalie indifferent between his (pure) strategies

  • Suppose Kicker plays Kick Left with probability p

Kicker's Optimal Choice of p

  • We want to find Kicker's optimal mixed strategy that leaves Goalie indifferent between his (pure) strategies

  • Suppose Kicker plays Kick Left with probability p

  • Goalie's expected payoff of playing Dive Left: 42p+7(1-p)

Kicker's Optimal Choice of p

  • We want to find Kicker's optimal mixed strategy that leaves Goalie indifferent between his (pure) strategies

  • Suppose Kicker plays Kick Left with probability p

  • Goalie's expected payoff of playing Dive Left: 42p+7(1-p)

  • Goalie's expected payoff of playing Dive Right: 5p+30(1-p)

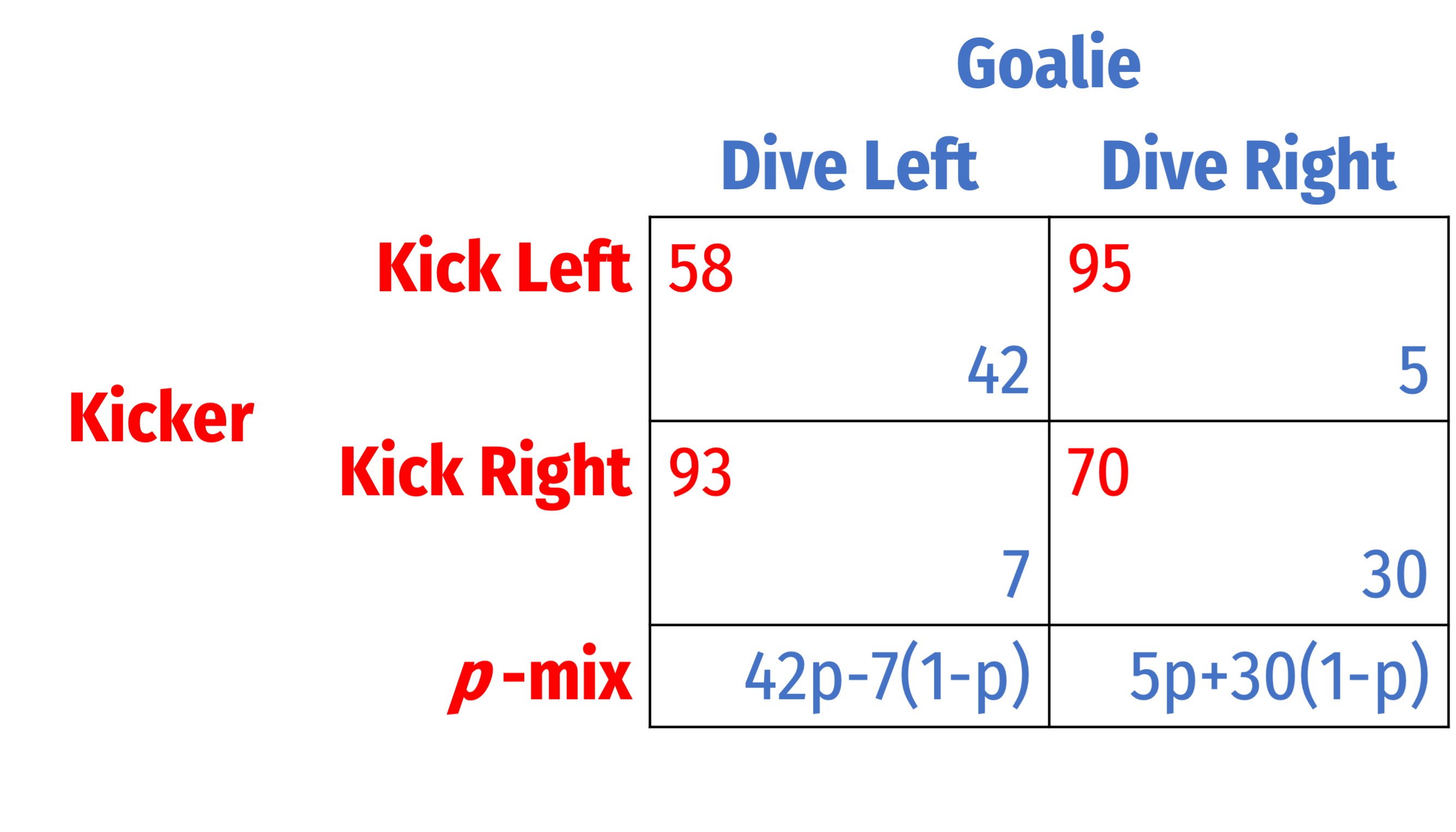
Kicker's Optimal Choice of p

  • We want to find Kicker's optimal mixed strategy that leaves Goalie indifferent between his (pure) strategies

  • Suppose Kicker plays Kick Left with probability p

  • Goalie's expected payoff of playing Dive Left: 42p+7(1-p)

  • Goalie's expected payoff of playing Dive Right: 5p+30(1-p)

  • What value of p would make Goalie indifferent between Dive Left and Dive Right?

    • i.e. E[Left]=E[Right]

Kicker's Optimal Choice of p, Graphically

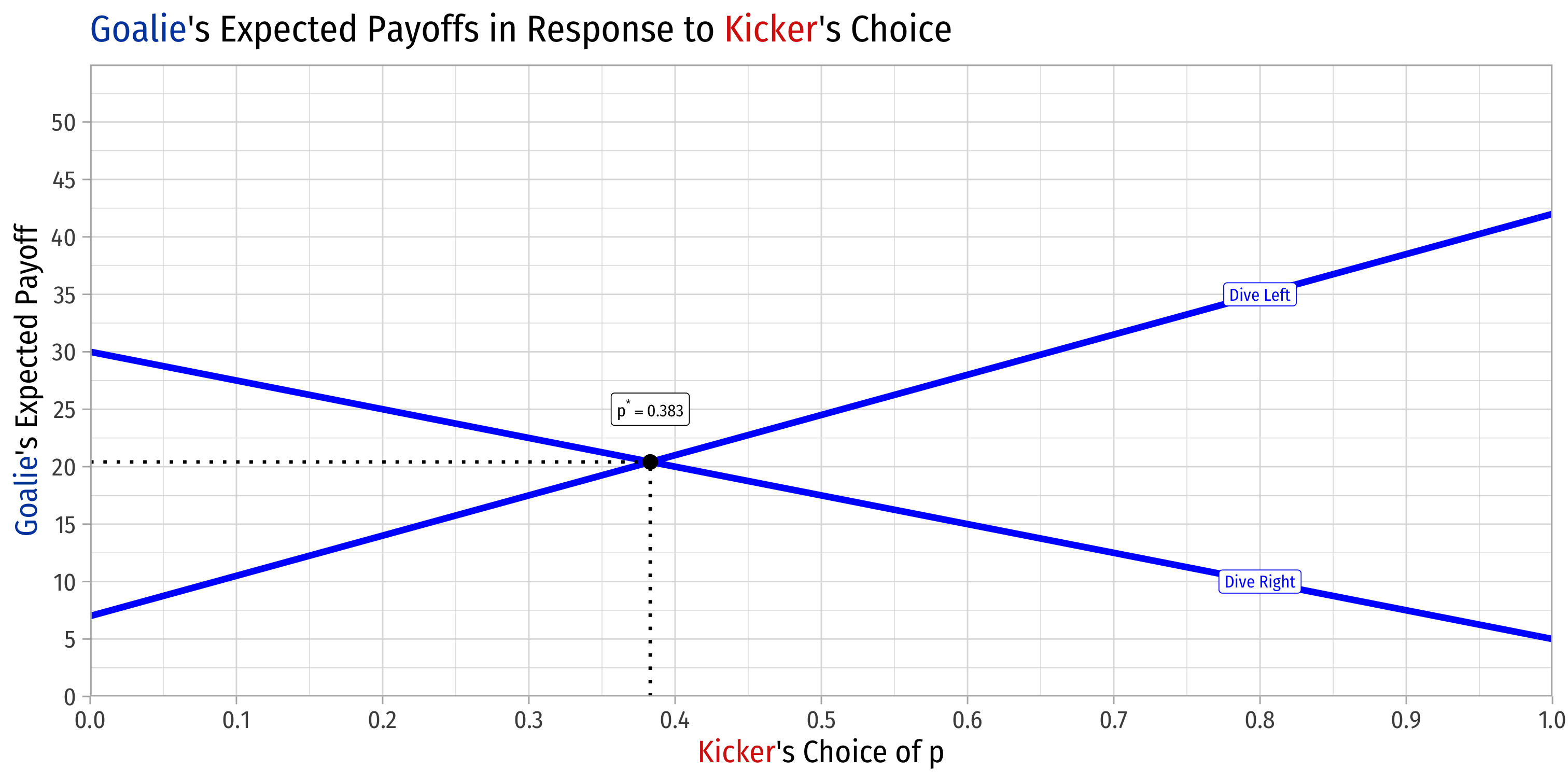
Kicker's Optimal Choice of p: Algebraically

  • Find value of p that equates Goalie's expected payoff of Dive Left and Dive Right:

E[Left]=E[Right]E[42p+7(1−p)]=E[5p+30(1−p)]

Kicker's Optimal Choice of p: Algebraically

  • Find value of p that equates Goalie's expected payoff of Dive Left and Dive Right:

E[Left]=E[Right]E[42p+7(1−p)]=E[5p+30(1−p)]

  • p⋆=0.383

Kicker's Optimal Choice of p: Algebraically

  • Find value of p that equates Goalie's expected payoff of Dive Left and Dive Right:

E[Left]=E[Right]E[42p+7(1−p)]=E[5p+30(1−p)]

  • p⋆=0.383

  • Kicker plays Kick Left with p=0.383 and Kick Right with 1−p=0.617

Kicker's Optimal Choice of p: Algebraically

  • Find value of p that equates Goalie's expected payoff of Dive Left and Dive Right:

E[Left]=E[Right]E[42p+7(1−p)]=E[5p+30(1−p)]

  • p⋆=0.383

  • Kicker plays Kick Left with p=0.383 and Kick Right with 1−p=0.617

    • Goalie's expected payoff of Dive Left: 42(0.383)+7(0.617)≈20.41

Kicker's Optimal Choice of p: Algebraically

  • Find value of p that equates Goalie's expected payoff of Dive Left and Dive Right:

E[Left]=E[Right]E[42p+7(1−p)]=E[5p+30(1−p)]

  • p⋆=0.383

  • Kicker plays Kick Left with p=0.383 and Kick Right with 1−p=0.617

    • Goalie's expected payoff of Dive Left: 42(0.383)+7(0.617)≈20.41

    • Goalie's expected payoff of Dive Right: 5(0.383)+30(0.617)≈20.41

Goalie's Optimal Choice of q

  • We want to find Goalie's optimal mixed strategy that leaves Kicker indifferent between his (pure) strategies

  • Suppose Goalie plays Dive Left with probability q

Goalie's Optimal Choice of q

  • We want to find Goalie's optimal mixed strategy that leaves Kicker indifferent between his (pure) strategies

  • Suppose Goalie plays Dive Left with probability q

  • Kicker's expected payoff of playing Dive Left: 58q+95(1-q)

Goalie's Optimal Choice of q

  • We want to find Goalie's optimal mixed strategy that leaves Kicker indifferent between his (pure) strategies

  • Suppose Goalie plays Dive Left with probability q

  • Kicker's expected payoff of playing Dive Left: 58q+95(1-q)

  • Kicker's expected payoff of playing Dive Right: 93q+70(1-q)

Goalie's Optimal Choice of q

  • We want to find Goalie's optimal mixed strategy that leaves Kicker indifferent between his (pure) strategies

  • Suppose Goalie plays Dive Left with probability q

  • Kicker's expected payoff of playing Dive Left: 58q+95(1-q)

  • Kicker's expected payoff of playing Dive Right: 93q+70(1-q)

  • What value of p would make Kicker indifferent between Kick Left and Kick Right?

    • i.e. E[Left]=E[Right]

Goalies's Optimal Choice of q, Graphically

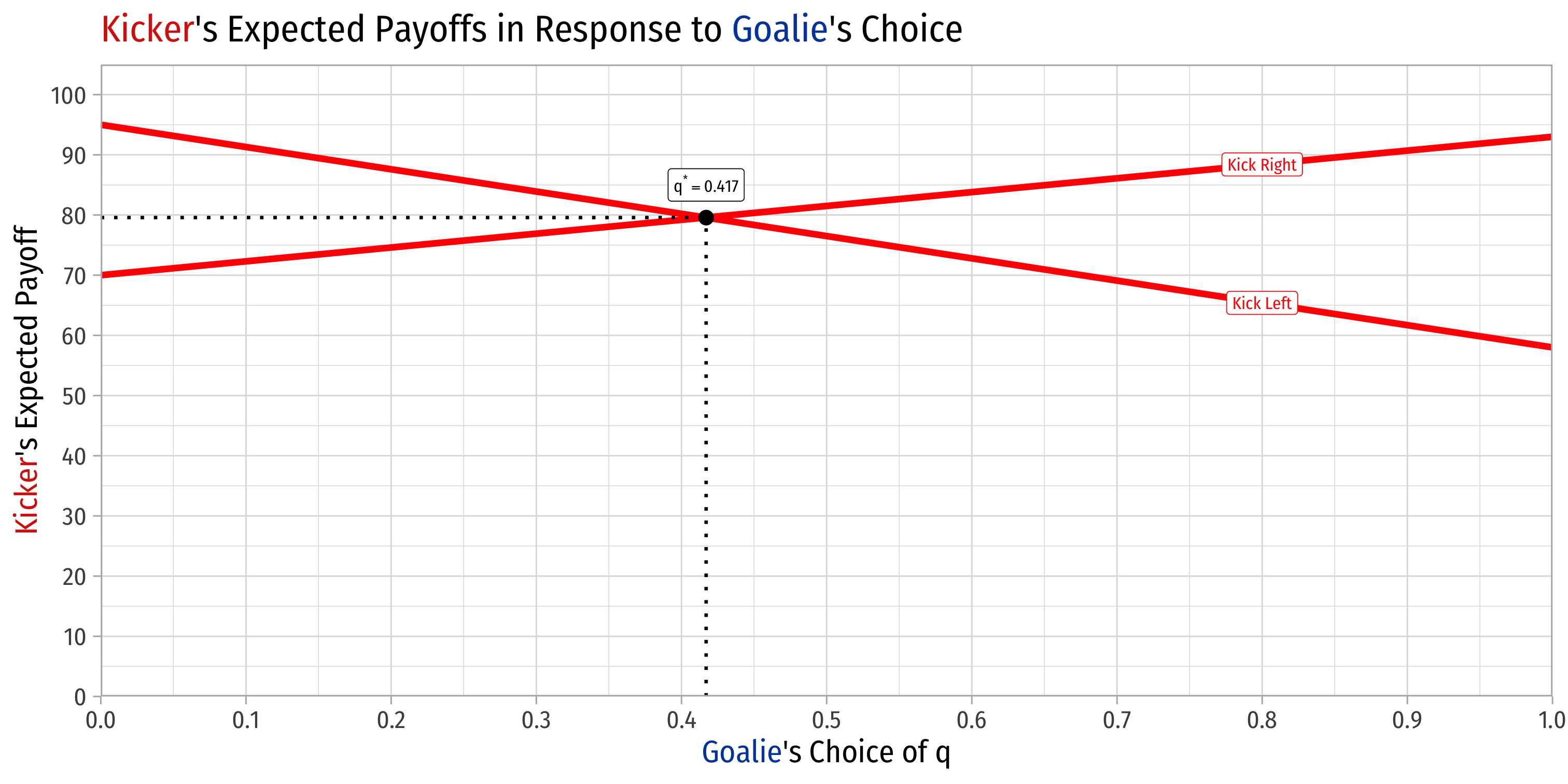
Goalie's Optimal Choice of q: Algebraically

  • Find value of q that equates Kicker's expected payoff of Kick Left and Kick Right:

E[Left]=E[Right]E[58q+95(1−q)]=E[93q+70(1−q)]

Goalie's Optimal Choice of q: Algebraically

  • Find value of q that equates Kicker's expected payoff of Kick Left and Kick Right:

E[Left]=E[Right]E[58q+95(1−q)]=E[93q+70(1−q)]

  • q⋆=0.417

Goalie's Optimal Choice of q: Algebraically

  • Find value of q that equates Kicker's expected payoff of Kick Left and Kick Right:

E[Left]=E[Right]E[58q+95(1−q)]=E[93q+70(1−q)]

  • q⋆=0.417

  • Goalie plays Dive Left with q=0.417 and Dive Right with 1−q=0.583

Goalie's Optimal Choice of q: Algebraically

  • Find value of q that equates Kicker's expected payoff of Kick Left and Kick Right:

E[Left]=E[Right]E[58q+95(1−q)]=E[93q+70(1−q)]

  • q⋆=0.417

  • Goalie plays Dive Left with q=0.417 and Dive Right with 1−q=0.583

    • Kicker's expected payoff of Kick Left: 58(0.417)+95(0.583)≈79.57

Goalie's Optimal Choice of q: Algebraically

  • Find value of q that equates Kicker's expected payoff of Kick Left and Kick Right:

E[Left]=E[Right]E[58q+95(1−q)]=E[93q+70(1−q)]

  • q⋆=0.417

  • Goalie plays Dive Left with q=0.417 and Dive Right with 1−q=0.583

    • Kicker's expected payoff of Kick Left: 58(0.417)+95(0.583)≈79.57

    • Kicker's expected payoff of Kick Right: 93(0.417)+70(0.583)≈79.57

Mixed Strategy Nash Equilibrium

  • Goalie is indifferent between Dive Left and Dive Right when Kicker plays Kick Left with p=0.383

  • Kicker is indifferent between Kick Left and Kick Right when Goalie plays Dive Left with q=0.417

Mixed Strategy Nash Equilibrium

  • Goalie is indifferent between Dive Left and Dive Right when Kicker plays Kick Left with p=0.383

  • Kicker is indifferent between Kick Left and Kick Right when Goalie plays Dive Left with q=0.417

  • Mixed Strategy Nash Equilibrium (MSNE): (p, q) = (0.383, 0.417)

Mixed Strategy Nash Equilibrium

  • Goalie is indifferent between Dive Left and Dive Right when Kicker plays Kick Left with p=0.383

  • Kicker is indifferent between Kick Left and Kick Right when Goalie plays Dive Left with q=0.417

  • Mixed Strategy Nash Equilibrium (MSNE): (p, q) = (0.383, 0.417)

    • Kicker's expected payoff: 79.57
    • Goalie's expected payoff: 20.41
    • Note they sum to 1!

p and q as Best Responses

  • p = pr(Kicker kicks Left)
  • q = pr(Goalie dives Left)

p and q as Best Responses

  • p = pr(Kicker kicks Left)

  • q = pr(Goalie dives Left)

  • Goalie's Best Response ={Rightif p<0.383Indifferentif p=0.383Leftif p>0.383

p and q as Best Responses

  • p = pr(Kicker kicks Left)

  • q = pr(Goalie dives Left)

  • Goalie's Best Response ={Rightif p<0.383Indifferentif p=0.383Leftif p>0.383

  • Kicker's Best Response ={Leftif q<0.417Indifferentif q=0.417Rightif q>0.417

p and q as Best Responses

  • p = pr(Kicker kicks Left)

  • q = pr(Goalie dives Left)

  • Goalie's Best Response ={Rightif p<0.383Indifferentif p=0.383Leftif p>0.383

  • Kicker's Best Response ={Leftif q<0.417Indifferentif q=0.4173Rightif q>0.417

  • Like any Nash equilibrium, players are playing mutual best responses to each other (probabilistically)

Goalie's Best Reponse (q) to p

Goalie's Best Response ={Rightif p<0.383Indifferentif p=0.383Leftif p>0.383

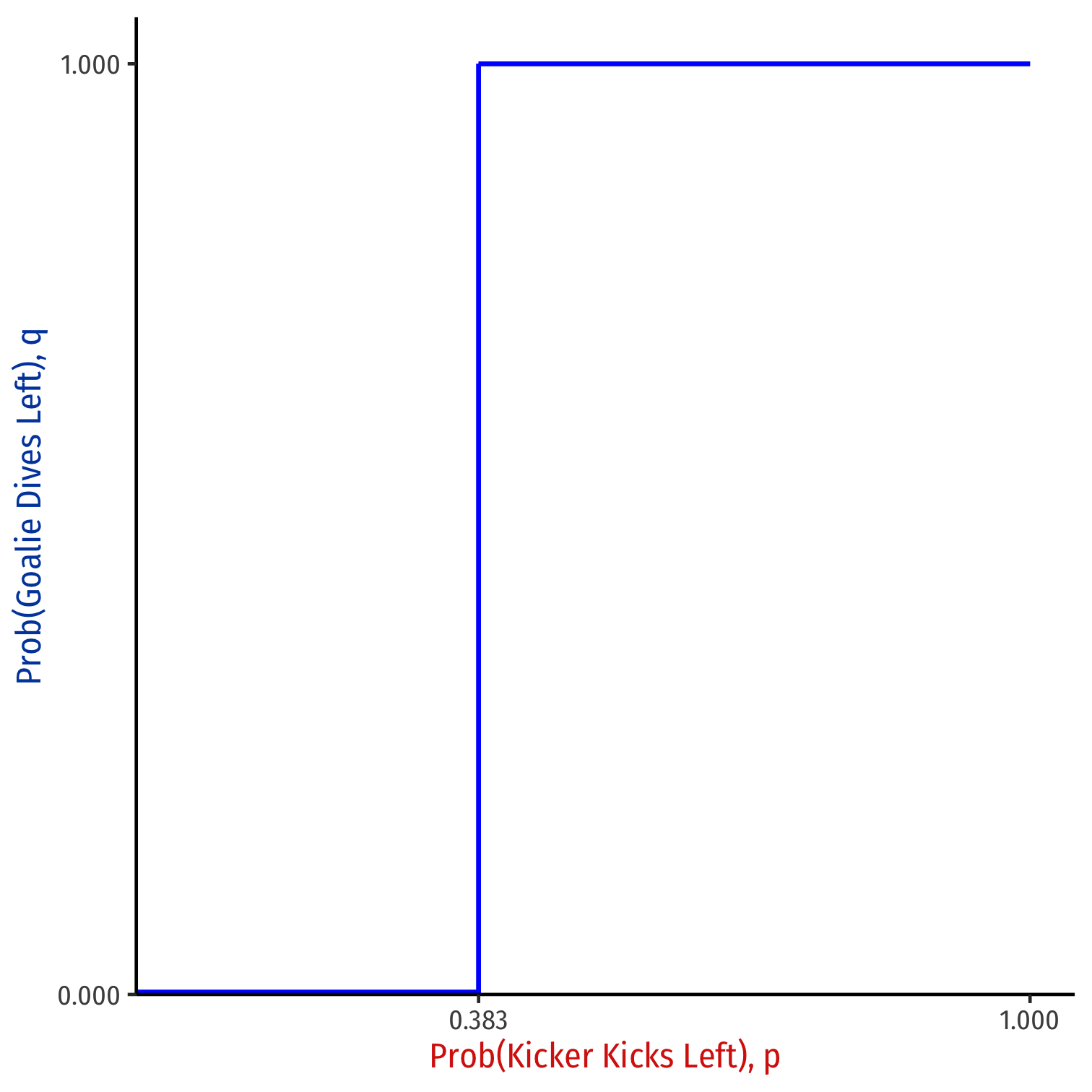
Kicker's Best Reponse (p) to q

  • Kicker's Best Response ={Leftif q<0.417Indifferentif q=0.4173Rightif q>0.417

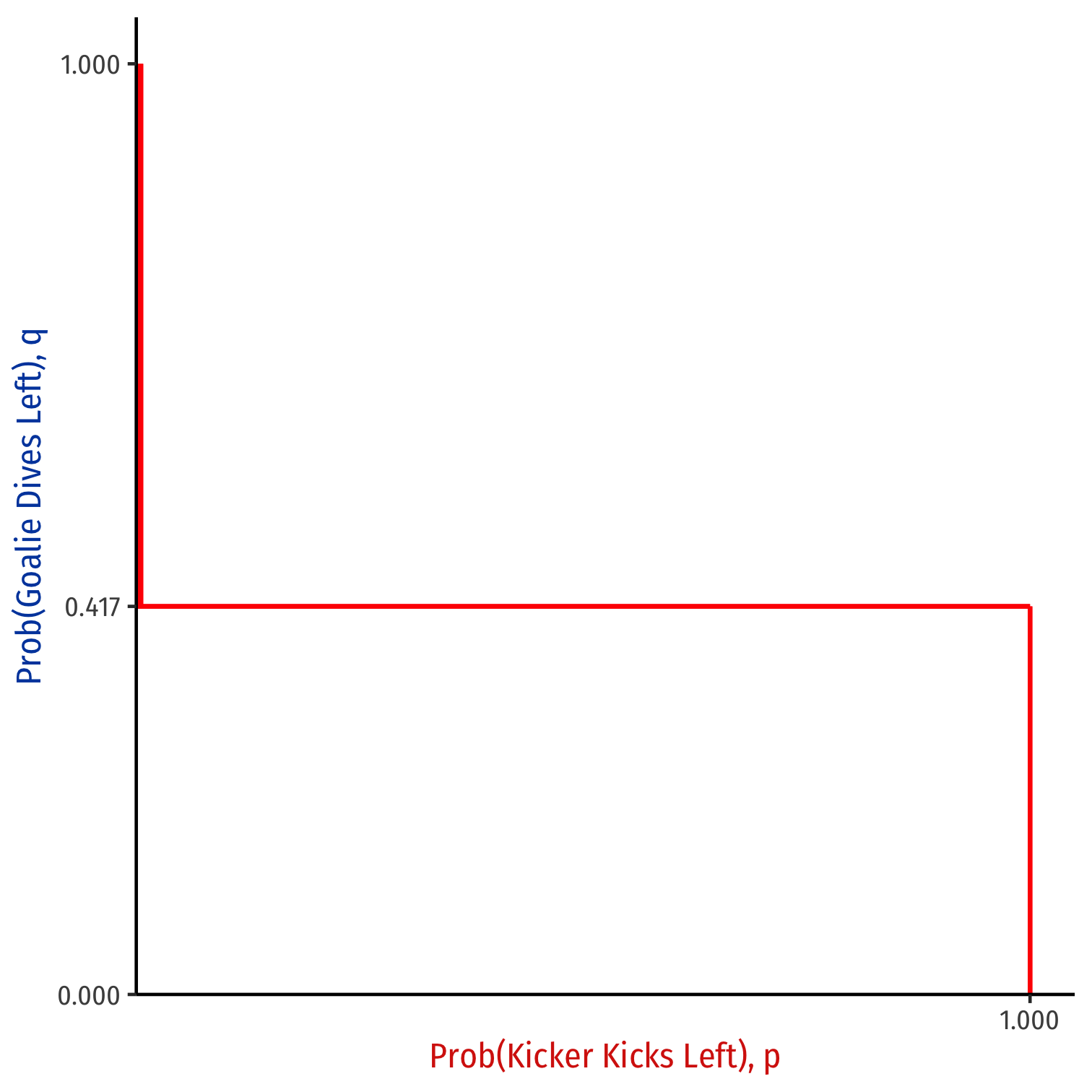
Mixed Strategy Nash Equilibrium

  • Like any Nash equilibrium, where best response functions intersect

Rock-Paper-Scissors I

  • A two player game with three strategies available to each

  • Graphically more difficult, but same principle to find MSNE

    • find probabilities that make opponent indifferent between their responses

  • Game is symmetric, so only need to find one player's optimal mixed strategy

Rock-Paper-Scissors II

  • Define for Column:
    • r= pr(Rock)
    • p= pr(Paper)
    • 1−r−p = pr(Scissors)

Rock-Paper-Scissors II

  • Define for Column:

    • r= pr(Rock)
    • p= pr(Paper)
    • 1−r−p = pr(Scissors)

  • Column must choose r,p that make Row indifferent between their strategies

Rock-Paper-Scissors II

  • List the expected payoffs to Row from Column's mix of r,p

  • Row's expected payoff must equal for all three strategies

    • So let's take any two and set them equal:

2r+p−1=p−r

Rock-Paper-Scissors II

  • List the expected payoffs to Row from Column's mix of r,p

  • Row's expected payoff must equal for all three strategies

    • So let's take any two and set them equal:

2r+p−1=p−r

  • r=13
  • p=13
  • (1−r−p)=13

Rock-Paper-Scissors II

  • MSNE: each player plays all three strategies with equal probability (13)

Coordination Games: PSNE and MSNE

MSNE in Coordination Games

  • The necessity of MSNE is easy to see for constant-sum games with no PSNE

  • But MSNE also exist for non-constant sum games, and for games with one or more PSNE

Assurance Game: MSNE

  • We know an assurance game has two PSNE

  • Let's solve for MSNE

Assurance Game: MSNE

  • Let p=pr(Harry goes to Whitaker)

  • Let q=pr(Sally goes to Whitaker)

Assurance Game: MSNE

  • Let p=pr(Harry goes to Whitaker)

  • Let q=pr(Sally goes to Whitaker)

Assurance Game: MSNE

  • Let p=pr(Harry goes to Whitaker)

  • Let q=pr(Sally goes to Whitaker)

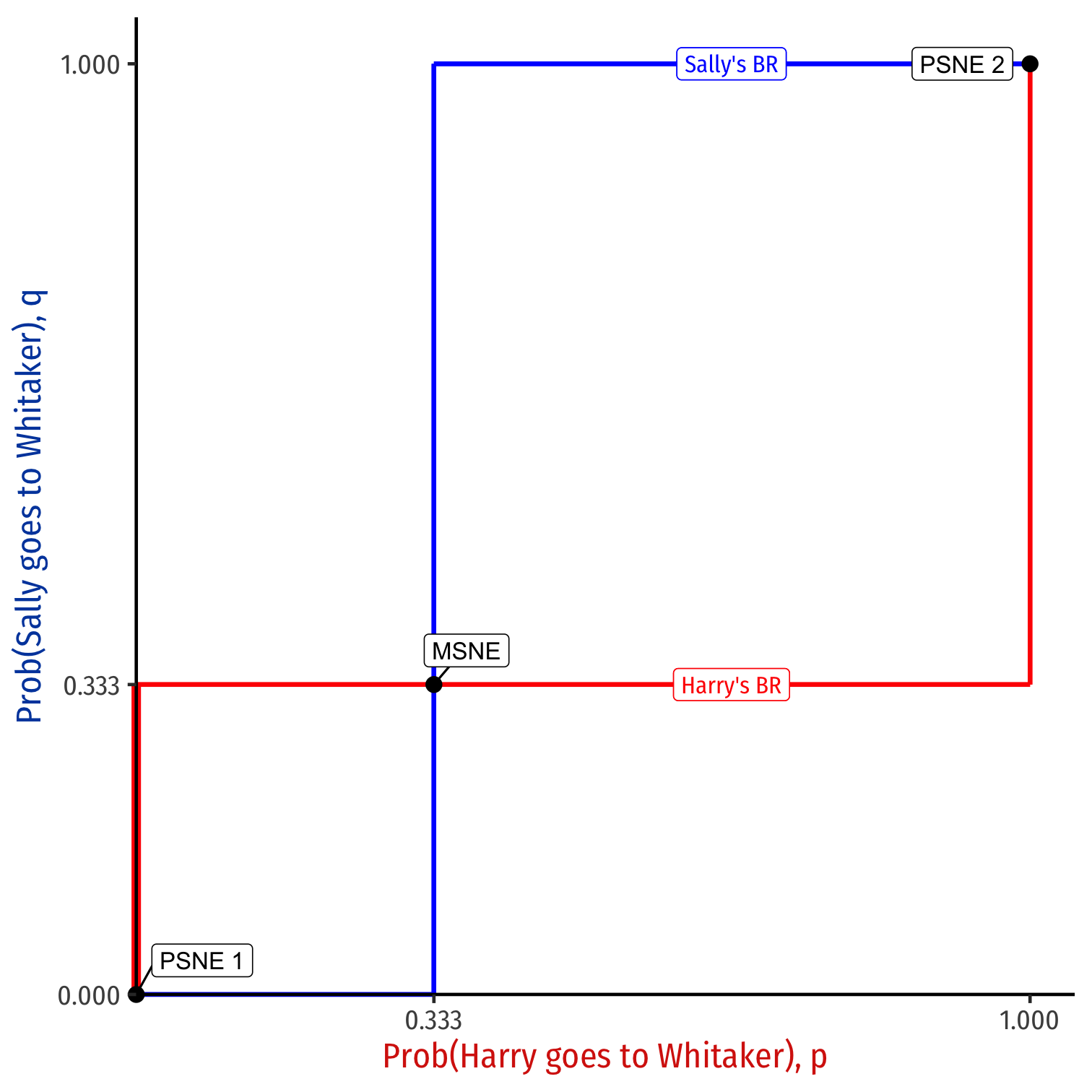
  • p⋆=13

  • q⋆=13

  • MSNE: (p, q) = (13,13)

Assurance Game: MSNE

  • Calculate expected payoffs to Harry and Sally with (p, q) MSNE

Assurance Game: MSNE

  • Calculate expected payoffs to Harry and Sally with (p, q) MSNE
    • Harry: 23
    • Sally: 23

Assurance Game: MSNE

  • Calculate expected payoffs to Harry and Sally with (p, q) MSNE

    • Harry: 23
    • Sally: 23

  • Problem: MSNE is even worse than either PSNE in this game!

    • Significant probability of going to different places
    • Also very fragile, anything >,<13 reverts to PSNE

Assurance Game: MSNE

  • Sally's BR ={Starbucksif p<13Indifferentif p=13Whitakerif p>13

  • Harry's BR ={Starbucksif q<13Indifferentif q=13Whitakerif q>13

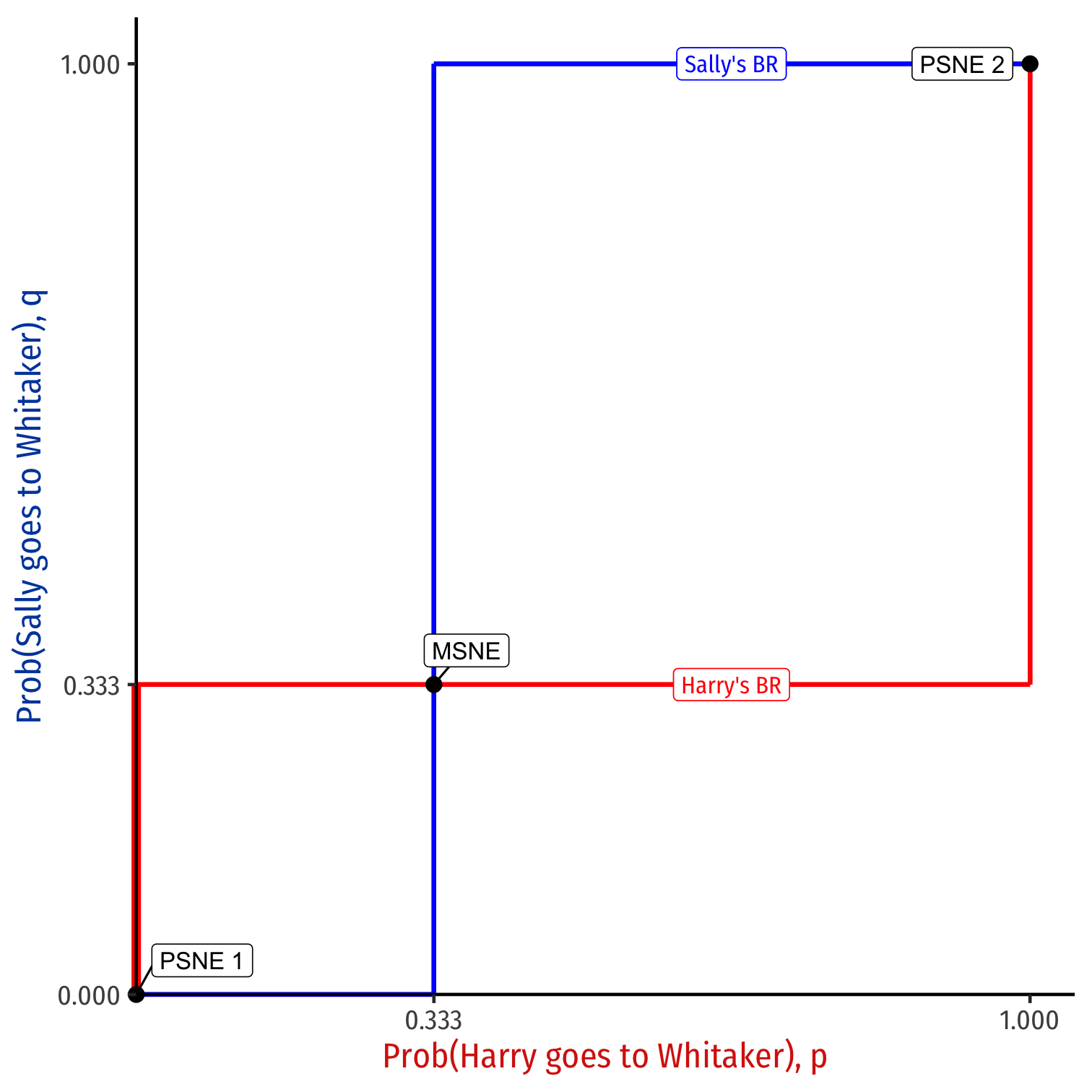
Assurance Game: MSNE

  • All intersections of best response functions are Nash equilibria

  • Interior solution: MSNE

  • Corner solutions: PSNE

    • PSNE are special cases of MSNE where p∈{0,1} and q∈{0,1}

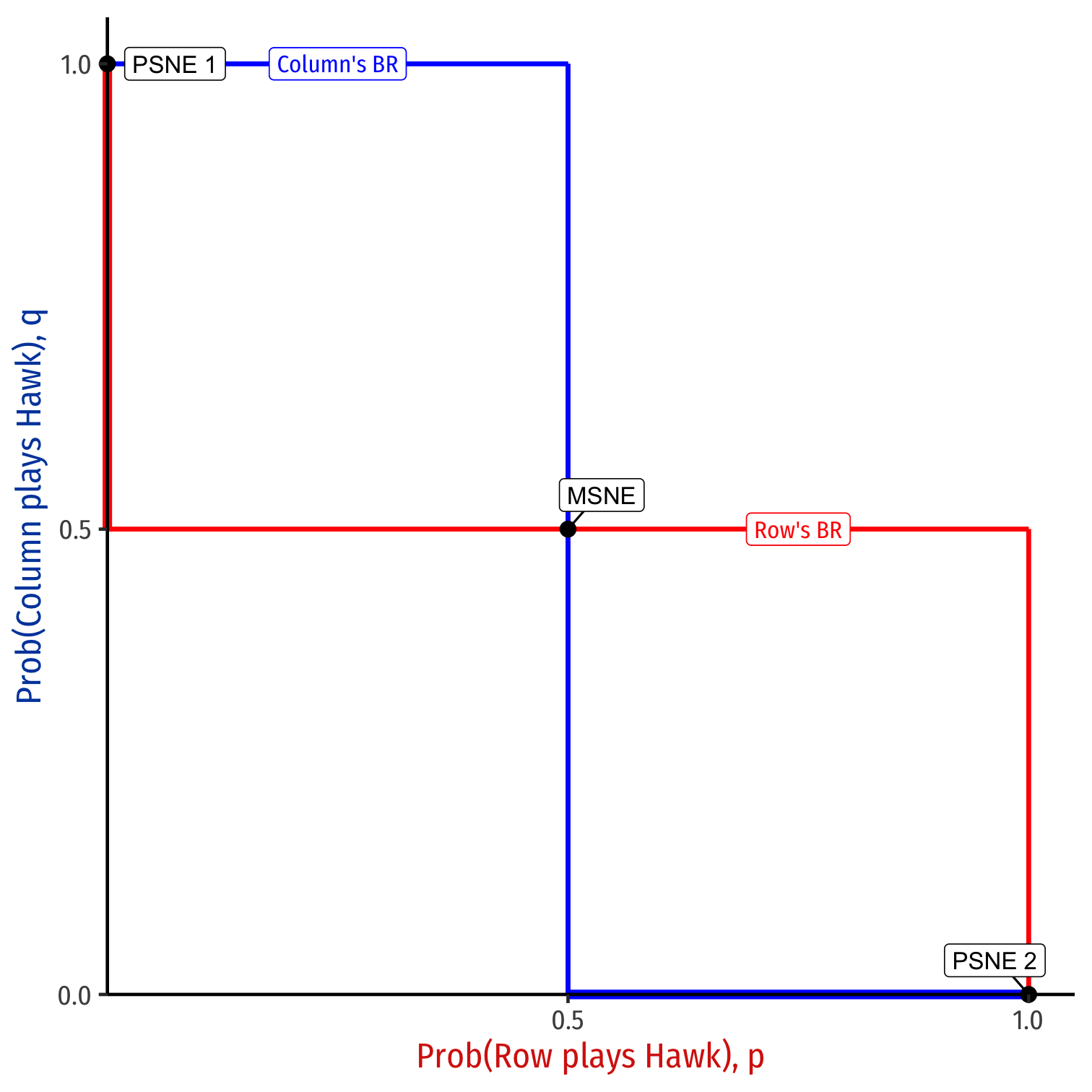
Chicken/Hawk-Dove Game: MSNE

  • Hawk-Dove/Chicken game: 2 PSNE

  • Let's solve for MSNE

Chicken/Hawk-Dove Game: MSNE

  • Let p=pr(Row plays Hawk)

  • Let q=pr(Column plays Hawk)

Chicken/Hawk-Dove Game: MSNE

  • Let p=pr(Row plays Hawk)

  • Let q=pr(Column plays Hawk)

Chicken/Hawk-Dove Game: MSNE

  • Let p=pr(Row plays Hawk)

  • Let q=pr(Column plays Hawk)

  • p⋆=0.5

  • q⋆=0.5

  • MSNE: (p, q) = (0.5,0.5)

Chicken/Hawk-Dove Game: MSNE

  • Calculate expected payoffs to Row and Column with (p, q) MSNE

Chicken/Hawk-Dove Game: MSNE

  • Calculate expected payoffs to Row and Column with (p, q) MSNE
    • Row: 0.5
    • Column: 0.5

Chicken/Hawk-Dove Game: MSNE

  • Calculate expected payoffs to Row and Column with (p, q) MSNE

    • Row: 0.5
    • Column: 0.5

  • Expected payoff in MSNE is:

    • better than PSNE when you're a dove against a hawk
    • worse than PSNE when you're a hawk against a dove

Chicken/Hawk-Dove Game: MSNE

  • Column's BR ={Hawkif p<0.5Indifferentif p=0.5Doveif p>0.5

  • Row's BR ={Hawkif q<0.5Indifferentif q=0.5Doveif q>0.5

Outline

When Pure Strategies Won't Work

MSNE in Constant Sum Games

Coordination Games: PSNE and MSNE

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
oTile View: Overview of Slides
Esc Back to slideshow