+ - 0:00:00
Notes for current slide
Notes for next slide

3.2 — Repeated Games

ECON 316 • Game Theory • Fall 2021

Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/gameF21
gameF21.classes.ryansafner.com

Outline

When Pure Strategies Won't Work

MSNE in Constant Sum Games

Coordination Games: PSNE and MSNE

Prisoners' Dilemma, Reprise

Prisoners' Dilemma, Reprise

Prisoners' Dilemma, Reprise

  • Not technically a Prisoners' Dilemma!

    • Game affected by Joker's threat to blow both of them up at midnight if nobody acts

  • Both players have a weakly-dominant strategy to Detonate

  • What is/are the Nash equilibrium/equilibria?

Prisoners' Dilemma, Reprise

  • A true prisoners' dilemma: a>b>c>d

  • Each player's preferences:

    • 1st best: you Defect, they Coop. ("temptation payoff")
    • 2nd best: you both Coop.
    • 3rd best: you both Defect
    • 4th best: you Coop., they Defect ("sucker's payoff")

  • Nash equilibrium: (Defect, Defect)

    • (Coop., Coop.) an unstable Pareto improvement

Prisoners' Dilemma: How to Sustain Cooperation?

  • We'll stick with these specific payoffs for this lesson

  • How can we sustain cooperation in Prisoners' Dilemma?

Repeated Games

Repeated Games: Finite and Infinite

  • Analysis of games can change when players encounter each other more than once

  • Repeated games: the same players play the same game multiple times, two types:

  • Players know the history of the game with each other

  • Finitely-repeated game: has a known final round

  • Infinitely-repeated game: has no (or an unknown) final round

Finitely-Repeated Games

Finitely-Repeated Prisoners' Dilemma

  • Suppose a prisoners' dilemma is played for 2 rounds

  • Apply backwards induction:

    • What should each player do in the final round?

Finitely-Repeated Prisoners' Dilemma

  • Suppose a prisoners' dilemma is played for 2 rounds

  • Apply backwards induction:

    • What should each player do in the final round?
    • Play dominant strategy: Defect
    • Knowing each player will Defect in round 2/2, what should they do in round 1?

Finitely-Repeated Prisoners' Dilemma

  • Suppose a prisoners' dilemma is played for 2 rounds

  • Apply backwards induction:

    • What should each player do in the final round?
    • Play dominant strategy: Defect
    • Knowing each player will Defect in round 2/2, what should they do in round 1?
      • No benefit to playing Cooperate
      • No threat punish Defection!

Finitely-Repeated Prisoners' Dilemma

  • Suppose a prisoners' dilemma is played for 2 rounds

  • Apply backwards induction:

  • Both Defect in round 1 (and round 2)

  • No value in cooperation over time!

Finitely-Repeated Prisoners' Dilemma

  • For any game with a unique PSNE in a one-shot game, as long as there is a known, finite end, Nash equilibrium is the same

Finitely-Repeated Prisoners' Dilemma

  • In experimental settings, we tend to see people cooperate in early rounds, but close to the final round (if not the actual final round), defect on each other

Infinitely-Repeated Games

Infinitely-Repeated Games

  • Finitely-repeated games are interesting, but rare

    • How often do we know for certain when a game/relationship we are in will end?

  • Some predictions for finitely-repeated games don't hold up well in reality

    • Ultimatum game, prisoners' dilemma

  • We often play games or are in relationships that are indefinitely repeated (have no known end), we call them infinitely-repeated games

Infinitely-Repeated Games

  • There are two nearly identical interpretations of infinitely repeated games:
    1. Players play forever, but discount (payoffs in) the future by a constant factor
    2. Each round the game might end with some constant probability

First Intepretation: Discounting the Future

  • Since we are dealing with payoffs in the future, we have to consider players' time preferences

  • Easiest to consider with monetary payoffs and the time value of money that underlies finance

PV=FV(1+r)t

FV=PV(1+r)t

Present vs. Future Goods

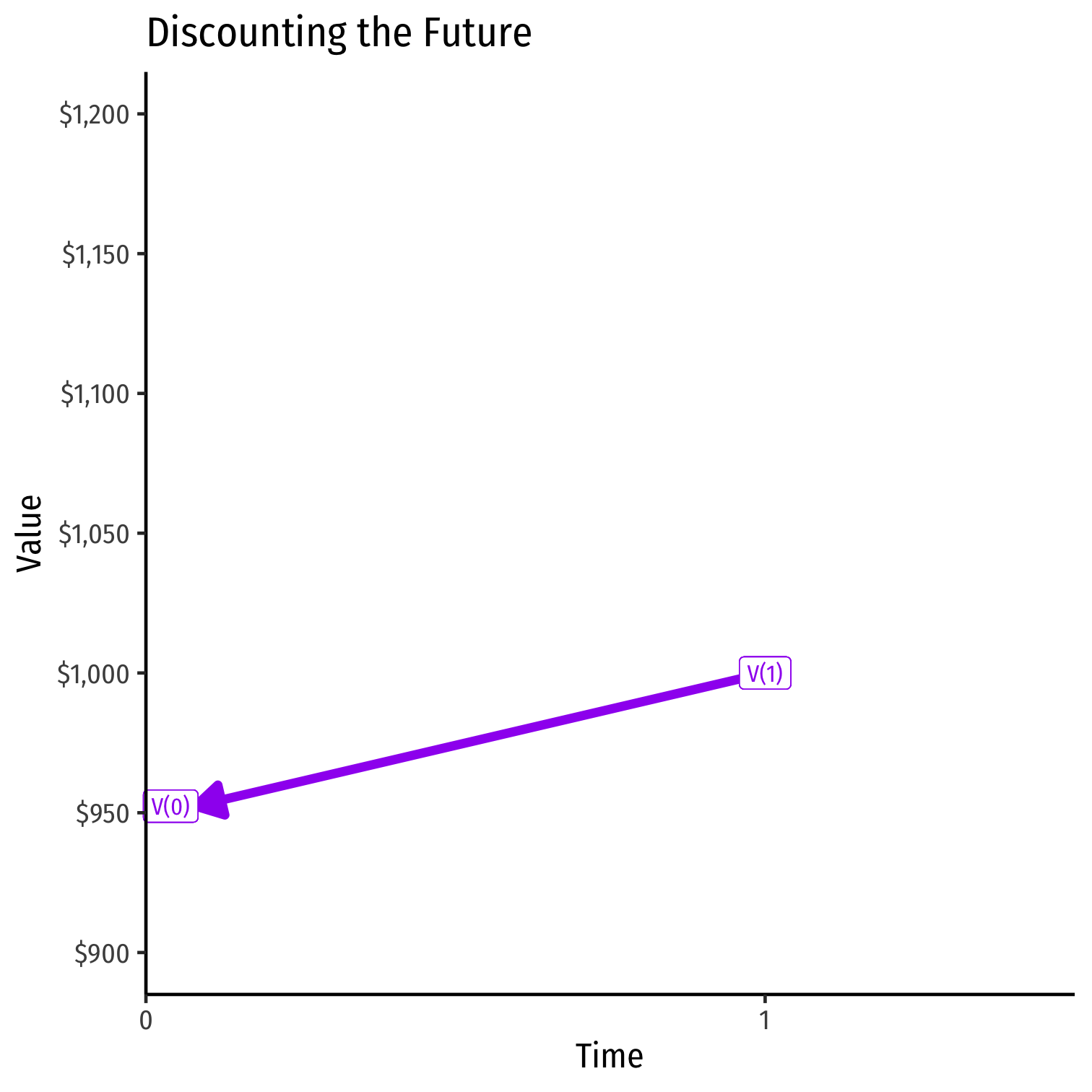
  • Example: what is the present value of getting $1,000 one year from now at 5% interest?

PV=FV(1+r)nPV=1000(1+0.05)1PV=10001.05PV=$952.38

Present vs. Future Goods

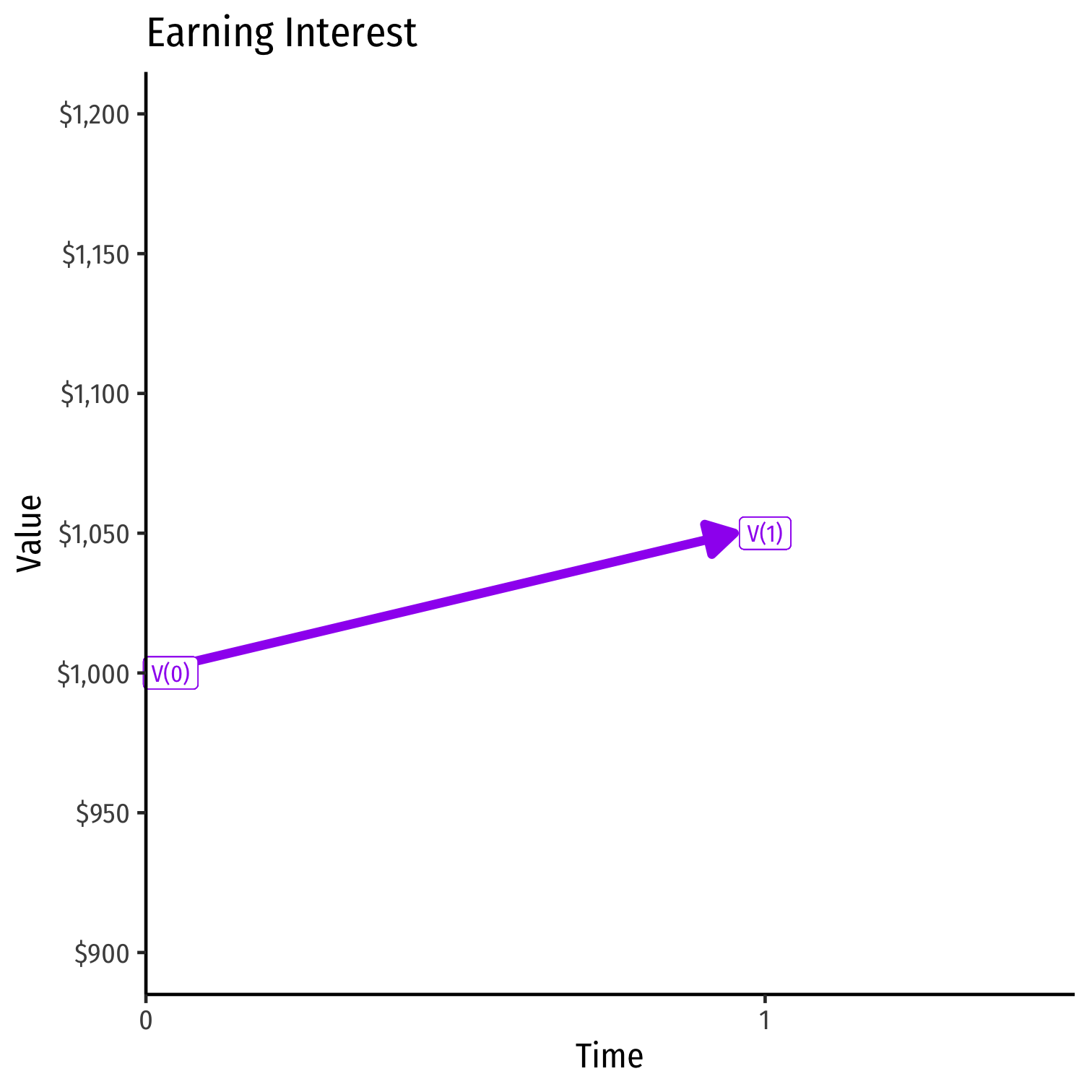
  • Example: what is the future value of $1,000 lent for one year at 5% interest?

FV=PV(1+r)nFV=1000(1+0.05)1FV=1000(1.05)FV=$1050

Discounting the Future

  • Suppose a player values $1 now as being equivalent to some amount with interest 1(1+r) one period later

    • i.e. $1 with an r% interest rate over that period

  • The “discount factor” is δ=11+r, the ratio that future value must be multiplied to equal present value

Discounting the Future

$1 now=δ$1 later

  • If δ is low (r is high)

    • Players regard future money as worth much less than present money, very impatient
    • Example: δ=0.20, future money is worth 20% of present money

  • If δ is high (r is low)

    • Players regard future money almost the same as present money, more patient
    • Example: δ=0.80, future money is worth 80% of present money

Discounting the Future

Example: Suppose you are indifferent between having $1 today and $1.10 next period

Discounting the Future

Example: Suppose you are indifferent between having $1 today and $1.10 next period

$1 today=δ$1.10 next period$1$1.10=δ0.91≈δ

Discounting the Future

Example: Suppose you are indifferent between having $1 today and $1.10 next period

$1 today=δ$1.10 next period$1$1.10=δ0.91≈δ

  • There is an implied interest rate of r=0.10

  • $1 at 10% interest yields $1.10 next period

δ=11+rδ=11.10 ≈0.91

Discounting the Future

  • Now consider an infinitely repeated game

Discounting the Future

  • Now consider an infinitely repeated game
    • If a player receives payoff p in every future round, the present value of this infinite payoff stream is

p(δ+δ2+δ3+⋯)

  • This is due to compounding interest over time

Discounting the Future

  • Now consider an infinitely repeated game
    • If a player receives payoff p in every future round, the present value of this infinite payoff stream is

p(δ+δ2+δ3+⋯)

  • This is due to compounding interest over time
    • This infinite sum converges to:

∞∑t=1=p1−δ

  • Thus, the present discounted value of receiving p in every future round is (p1−δ)

Prisoners' Dilemma, Infinitely Repeated

  • With these payoffs, the value of both cooperating forever is (31−δ)
  • Value of both defecting forever is (21−δ)

Alternatively: Game Continues Probabilistically

  • Alternate interpretation: game continues with some (commonly known among the players) probability θ each round

  • Assume this probability is independent between rounds (i.e. one round continuing has no influence on the probability of the next round continuing, etc)

Alternatively: Game Continues Probabilistically

  • Then the probability the game is played T rounds from now is θT

  • A payoff of p in every future round has a present value of p(θ+θ2+θ3+⋯)=(p1−θ)

  • This is similar to discounting of future payoffs; equivalent if θ=δ

Strategies in Infinitely Repeated Games

  • Recall, a strategy is a complete plan of action that describes how you will react under all possible circumstances (i.e. moves by other players)

    • i.e. "if other player plays x, I'll play a, if they play y, I'll play b, if, ..., etc"
    • think about it as a(n infinitely-branching) game tree, “what will I do at each node where it is my turn?”

  • For an infinitely-repeated game, an infinite number of possible strategies exist!

  • We will examine a specific set of contingent or trigger strategies

Trigger Strategies

  • Consider one (the most important) trigger strategy for an infinitely-repeated prisoners' dilemma, the “Grim Trigger” strategy:

    • On round 1: Cooperate
    • Every future round: so long as the history of play has been (Coop, Coop) in every round, play Cooperate. Otherwise, play Defect forever.

  • “Grim” trigger strategy leaves no room for forgiveness: one deviation triggers infinite punishment, like the sword of Damocles

Payoffs in Grim Trigger Strategy

  • If you are playing the Grim Trigger strategy, consider your opponent's incentives:
    • If you both Cooperate forever, you receive an infinite payoff stream of 3 per round

3+3δ+3δ2+3δ3+⋯+3δ∞=31−δ

Payoffs in Grim Trigger Strategy

  • This strategy is a Nash equilibrium as long there's no incentive to deviate:

Payoff to cooperation>Payoff to one-time defection31−δ>4+2δ1−δδ>0.5

  • If δ>0.5, then player will cooperate and not defect

Payoffs in Grim Trigger Strategy

  • δ>0.5 is sufficient to sustain cooperation under the grim trigger strategy
    • This is the most extreme strategy with the strongest threat

Payoffs in Grim Trigger Strategy

  • Two interpretations of δ>0.5 as a sufficient condition for cooperation:
  1. δ as sufficiently high discount rate
    • Players are patient enough and care about the future (reputation, etc), will not defect
  2. δ as sufficiently high probability of repeat interaction
    • Players expect to encounter each other again and play future games together

Other Trigger Strategies

  • "Grim Trigger" strategy is, well, grim: a single defection causes infinite punishment with no hope of redemption
    • Very useful in game theory for understanding the “worst case scenario” or the bare minimum needed to sustain cooperation!
    • Empirically, most people aren't playing this strategy in life
    • Social cooperation hangs on by a thread: what if the other player makes a mistake? Or you mistakenly think they Defected?
  • There are “nicer” trigger strategies

"Nicer" Strategies

  • Consider a "Forgiving Trigger" strategy:
    • On round 1: Cooperate
    • Every future round: so long as the history of play has been (Coop, Coop) in every round, play Cooperate. Otherwise, play Defect for 3 rounds
      • Punishment, but lasts for 3 rounds, then reverts to Cooperation

"Nicer" Strategies

  • Consider the "Tit for Tat" strategy:
    • On round 1: Cooperate
    • Every future round: Play the strategy that the other player played last round
      • Example: if they Cooperated, play Cooperate; if they Defected, play Defect

"Nicer" Strategies

  • Consider the "Tit for 2 Tats" strategy:
    • On round 1: Cooperate
    • Every future round: Cooperate, unless the other player has played Defect twice, then play Defect

Outline

When Pure Strategies Won't Work

MSNE in Constant Sum Games

Coordination Games: PSNE and MSNE

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
oTile View: Overview of Slides
Esc Back to slideshow