4.1 — Subgame Perfection
ECON 316 • Game Theory • Fall 2021
Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/gameF21
gameF21.classes.ryansafner.com
Subgame Perfection
A Motivating Example
Suppose I announce that if any of you were late, I would give you an F
If you believe my threat, you will arrive on time, and I never have to carry out my threat
Sounds like a Nash equilibrium:
- I get what I want at no cost to me
- You prefer being in class on time to failing
- Nobody wants to change

A Motivating Example
Implausible prediction: I would not actually want to carry out my threat if it came to it!
- Big confrontation, you could complain to Dept. chair, Provost, etc
A problem of “out-of-equilibrium” play
- How can a threat I will never carry out change your behavior?
- I can optimally choose bizarre behavior in situations I know will never happen!

A Motivating Example
- BUT: if you know what would happen in those unlikely scenarios, that does affect your behavior for things that normally happen
- namely, if you know I will not actually fail you for coming late, you will sometimes come late

Motivating Example
This lesson is about the effects of threats and promises
Must learn another major refinement of Nash equilibrium
First, return to seqential games
Continue with assumption of perfect information (soon we will consider imperfect information)

Motivating Example
A new solution concept:
Subgame perfect Nash equilibrium (SPNE): selects only Nash equilibria sustained by credible threats and promises, and rules out non-credible threats/promises
- Formal definition: a set of strategies is SP if it induces a Nash equilibrium in every subgame of a game
First, let’s understand what we mean by “subgame”

Subgames
Subgames
A subgame is any portion of a game that contains one initial note and all of its successor nodes
- e.g. any decision node initiates its own subgame through to the terminal nodes
- The game itself counts as a subgame
Idea: analyze a subgame as a game itself and ignore any history in the overall game and find what is optimal in each subgame

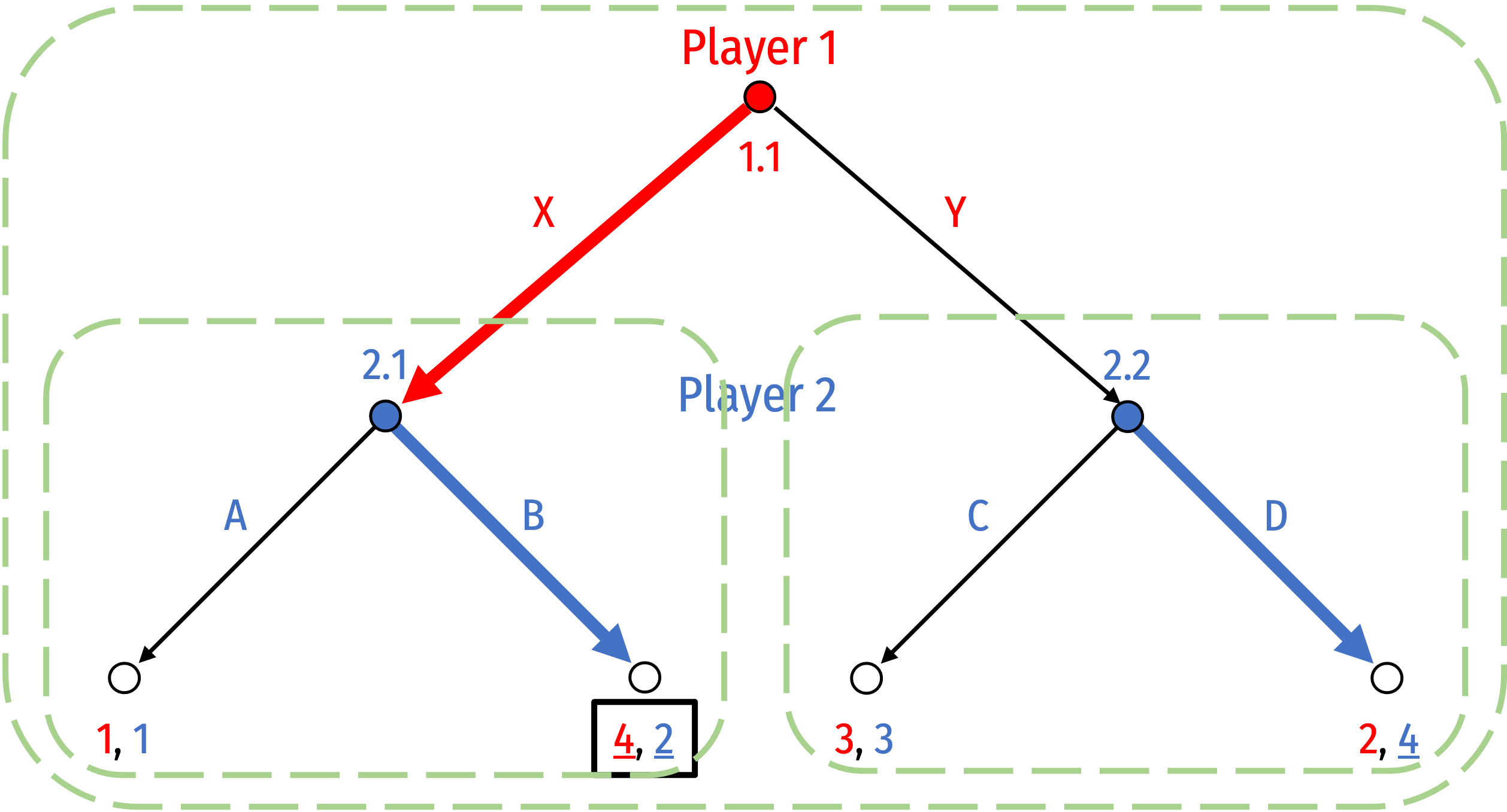
Subgames: Example
- In this example, there are 3 subgames:
- The full game itself (initiated by Player 1's decision node 1.1)
- Subgame initiated by Player 2's decision node 2.1
- Subgame initiated by Player 2's decision node 2.2
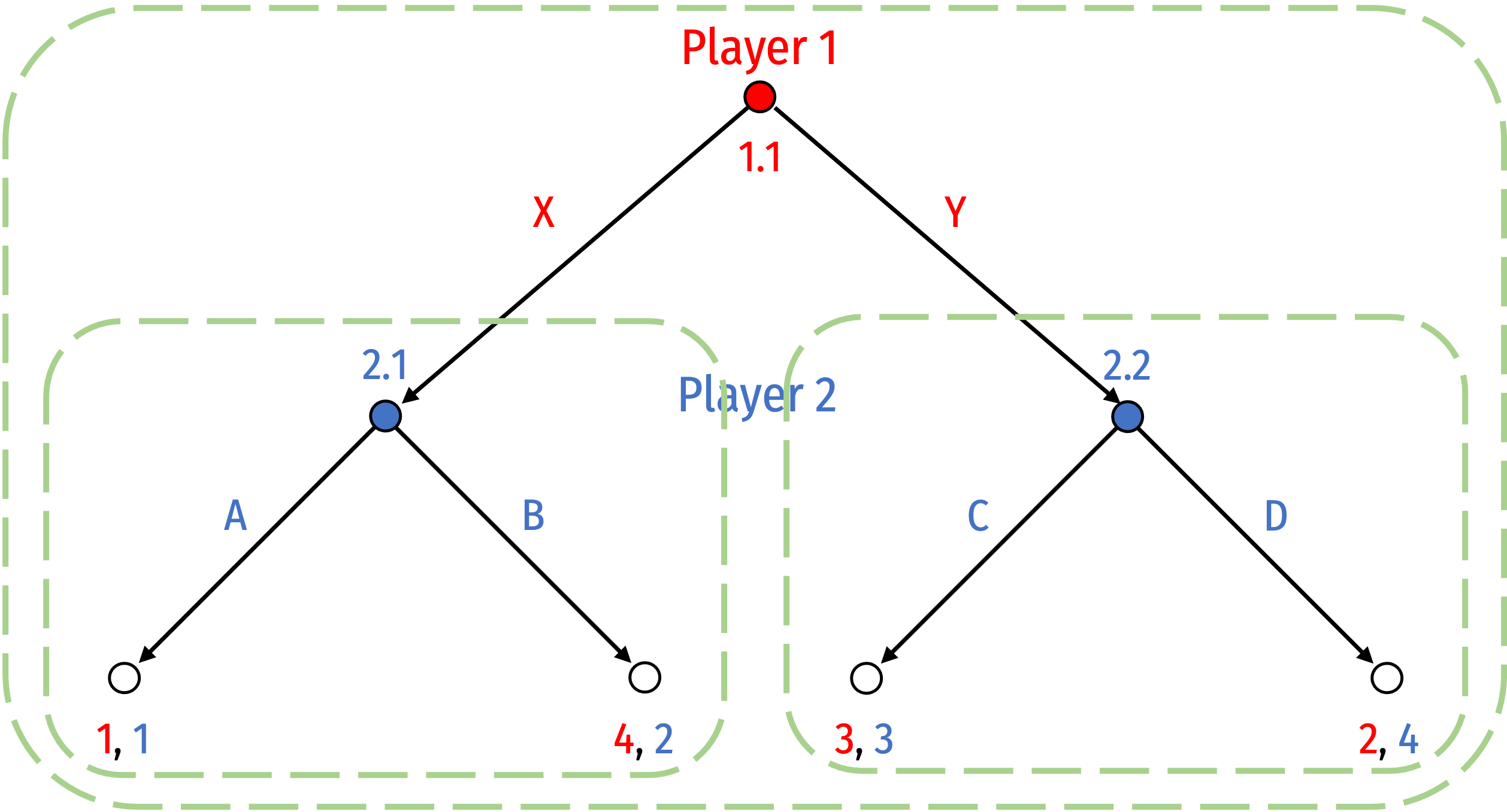
Aside: Subgames Can't Break Information Sets
Subgames cannot “break” information sets
- Indicated by dashed line: Player 2 does not know what Player 1 chose (consider it a simultaneous game)
- More on information later
Players must know which subgame they are in, so a subgame cannot “break” an information set
- Player 2 here would not know what Player 1 did, so Player 1 can’t make a decision; could not “ignore history”
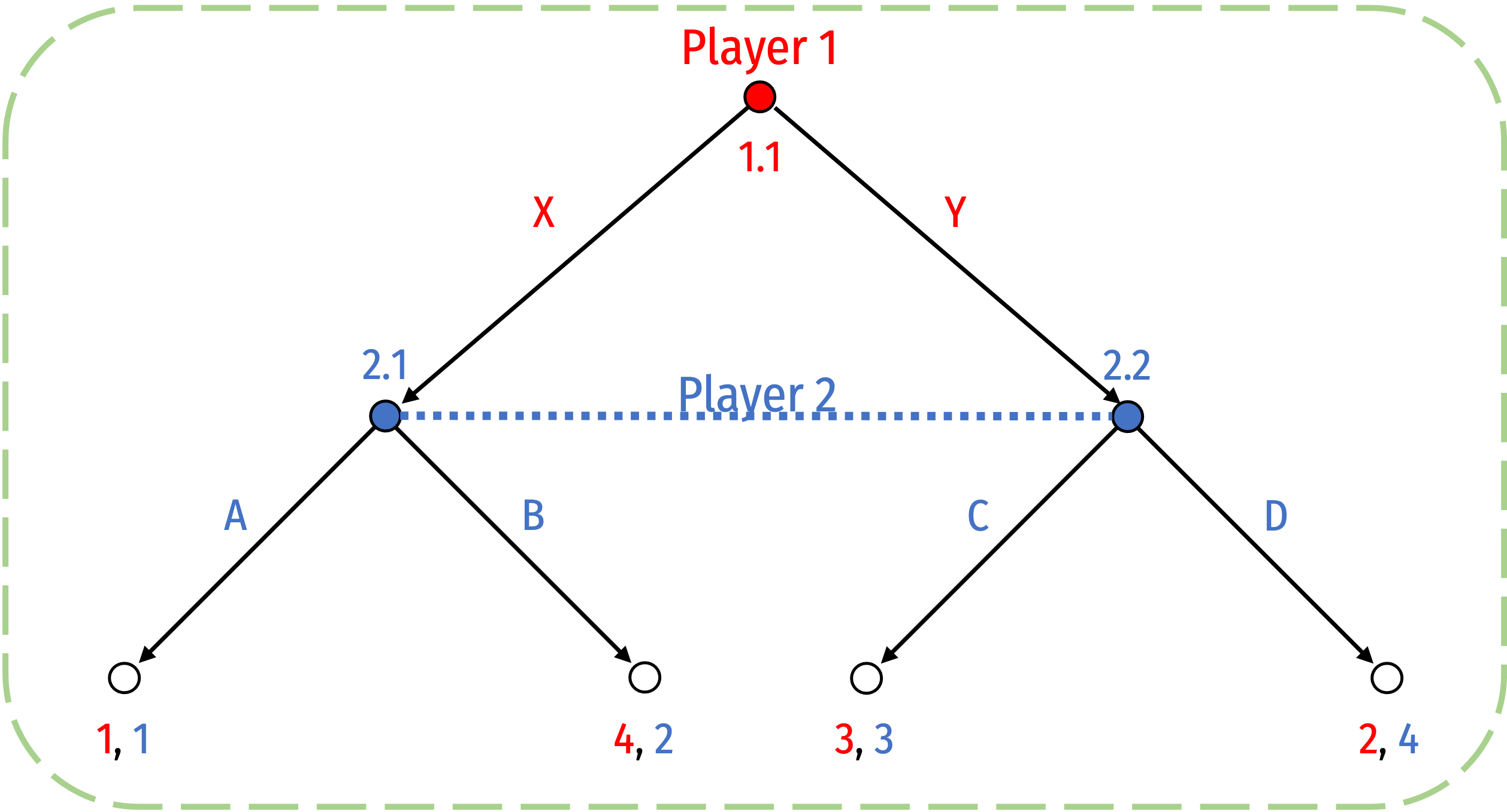
(Review) Strategies in this Example
Recall we defined a strategy as a complete plan of what a player will do at every decision node they (might) face
Player 1 has 1 decision (1.1) with 2 choices, so \(2^1\) possible strategies:
- X at (1.1)
- Y at (1.1)

(Review) Strategies in this Example
Recall we defined a strategy as a complete plan of what a player will do at every decision node they (might) face
Player 1 has 1 decision (1.1) with 2 choices, so \(2^1\) possible strategies:
- X at (1.1)
- Y at (1.1)
Player 2 has 2 decision (2.1, 2.2) with 2 choices at each, so \(2^2\) possible strategies:
- A at (2.1); C at (2.2)
- A at (2.1); D at (2.2)
- B at (2.1); C at (2.2)
- B at (2.1); D at (2.2)

Converting Between Sequential and Normal Form
- We can convert any sequential game in extended form (game tree) into a normal game (payoff matrix)
- Harder to go the other way around!

Converting Between Sequential and Normal Form
We can convert any sequential game in extended form (game tree) into a normal game (payoff matrix)
- Harder to go the other way around!
Payoff matrix of outcomes of all possible combinations of strategies for each player


Converting Between Sequential and Normal Form
- Solve the normal form for Nash equilibria


Converting Between Sequential and Normal Form
- Nash equilibria:
- {Y, (A,D)}
- {X, (B,C)}
- {X, (B,D)}

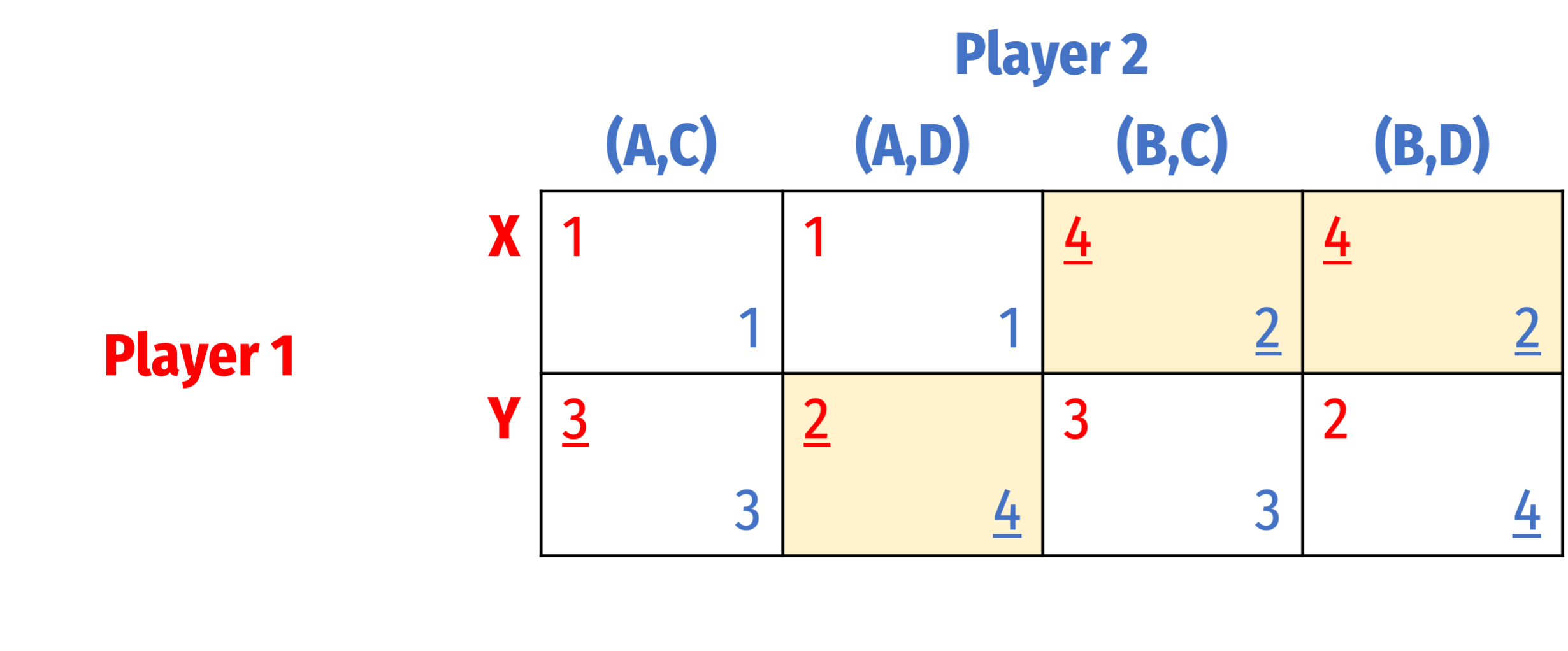
Converting Between Sequential and Normal Form
Nash equilibria:
- {Y, (A,D)}
- {X, (B,C)}
- {X, (B,D)}
But remember, this is a sequential game! Which of these Nash equilibria is sequentially-rational?


Rollback Equilibrium
Solve for rollback equilibrium via backwards induction
A process of considering “sequential rationality”:
“If I play x, my opponent will respond with y; given their response, do I really want to play x? ...”


Converting Between Sequential and Normal Form
Nash equilibria:
- {Y, (A,D)}
- {X, (B,C)}
- {X, (B,D)}
Rollback equilibrium: {X, (B,D)}


Converting Between Sequential and Normal Form
Nash equilibria:
- {Y, (A,D)}
- {X, (B,C)}
- {X, (B,D)}
Even though there are three Nash equilibria, only one is subgame perfect
- Player 1 and Player 2 are playing {X, (B,D)} respectively causes a Nash equilibrium in every subgame


Converting Between Sequential and Normal Form
- Nash equilibria:
- {Y, (A,D)}
- {X, (B,C)}
- {X, (B,D)}
- Consider the first NE: {Y, (A,D)}
- Not on the equilibrium path of play
- Not sequentially rational: if Player 1 had played X (for whatever reason), Player 2 would want to switch from playing A to playing B at 2.1!
- Thus, this strategy is not a NE in subgame initiated at node 2.1 (Player 2 would want to change strategies)
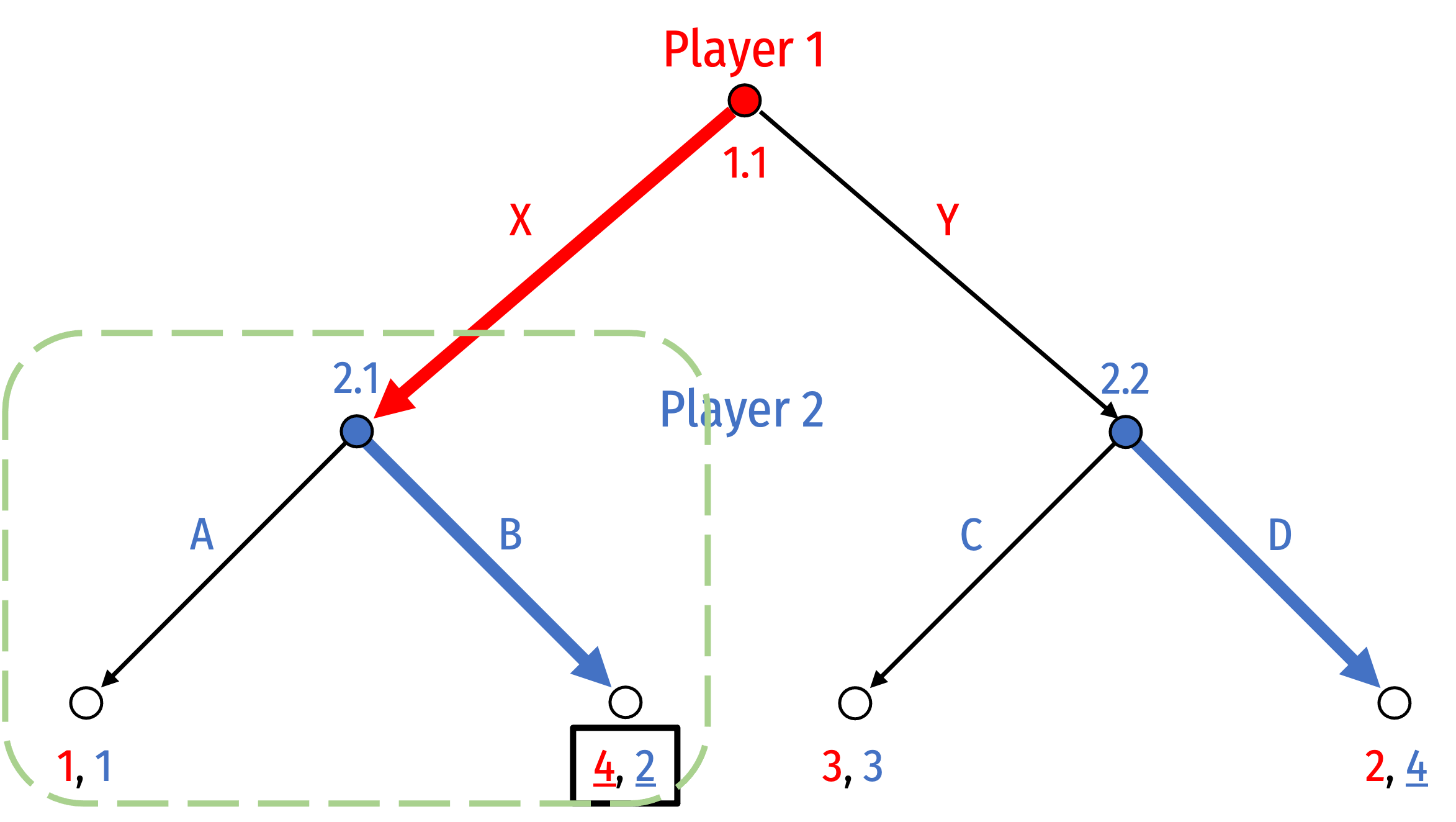

Converting Between Sequential and Normal Form
- Nash equilibria:
- {Y, (A,D)}
- {X, (B,C)}
- {X, (B,D)}
- Consider the second NE: {X, (B,C)}
- Not on the equilibrium path of play
- Not sequentially rational: if Player 1 had played Y (for whatever reason), Player 2 would want to switch from playing C to playing D at 2.2!
- Thus, this strategy is not a NE in subgame initiated at node 2.2 (Player 2 would want to change strategies)


Converting Between Sequential and Normal Form
- Nash equilibria:
- {Y, (A,D)}
- {X, (B,C)}
- {X, (B,D)}
- Consider the third NE: {X, (B,D)}
- On the equilibrium path of play
- Sequentially rational: these strategies lead to a NE in every subgame!
- Conveniently: the “rollback equilibrium” is always subgame perfect

Converting Between Sequential and Normal Form
Subgame perfection rules out non-credible threats or promises
Depending on context, Player 2 might threaten/promise that they will play C if Player 1 plays Y
- But if that subgame were reached, Player 2 would not play C, they would want to play D!
- i.e. not a credible claim


Entry Game Example
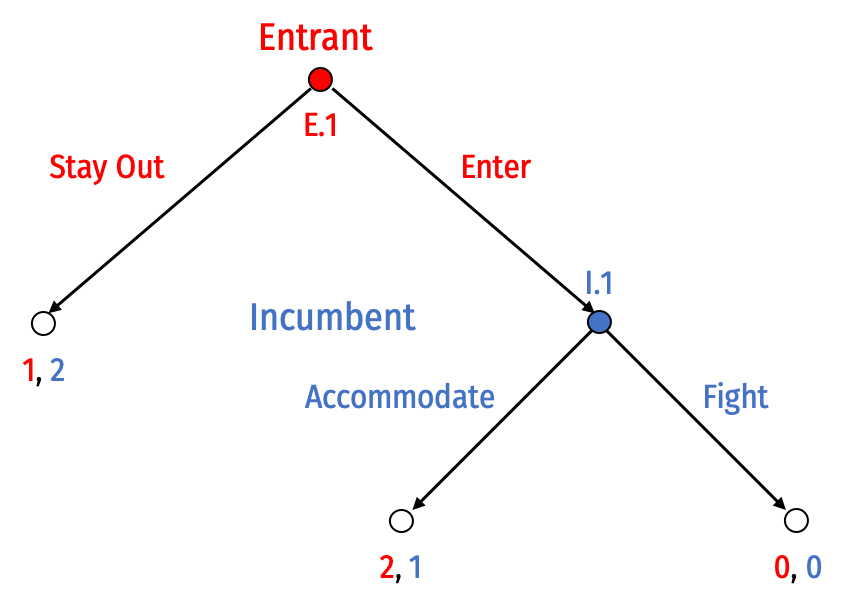
Entry Game: Extensive Form
- Consider an Entry Game, a sequential game played between a potential Entrant and an Incumbent
Entry Game: (Pure) Strategies
Entrant has 2 pure strategies:
- Stay Out at E.1
- Enter at E.1
Incumbent has 2 pure strategies:
- Accommodate at I.1
- Fight at I.1

Entry Game: Backward Induction
- Rollback/Subgame Perfect Nash Equilibrium:
(Enter, Accommodate)

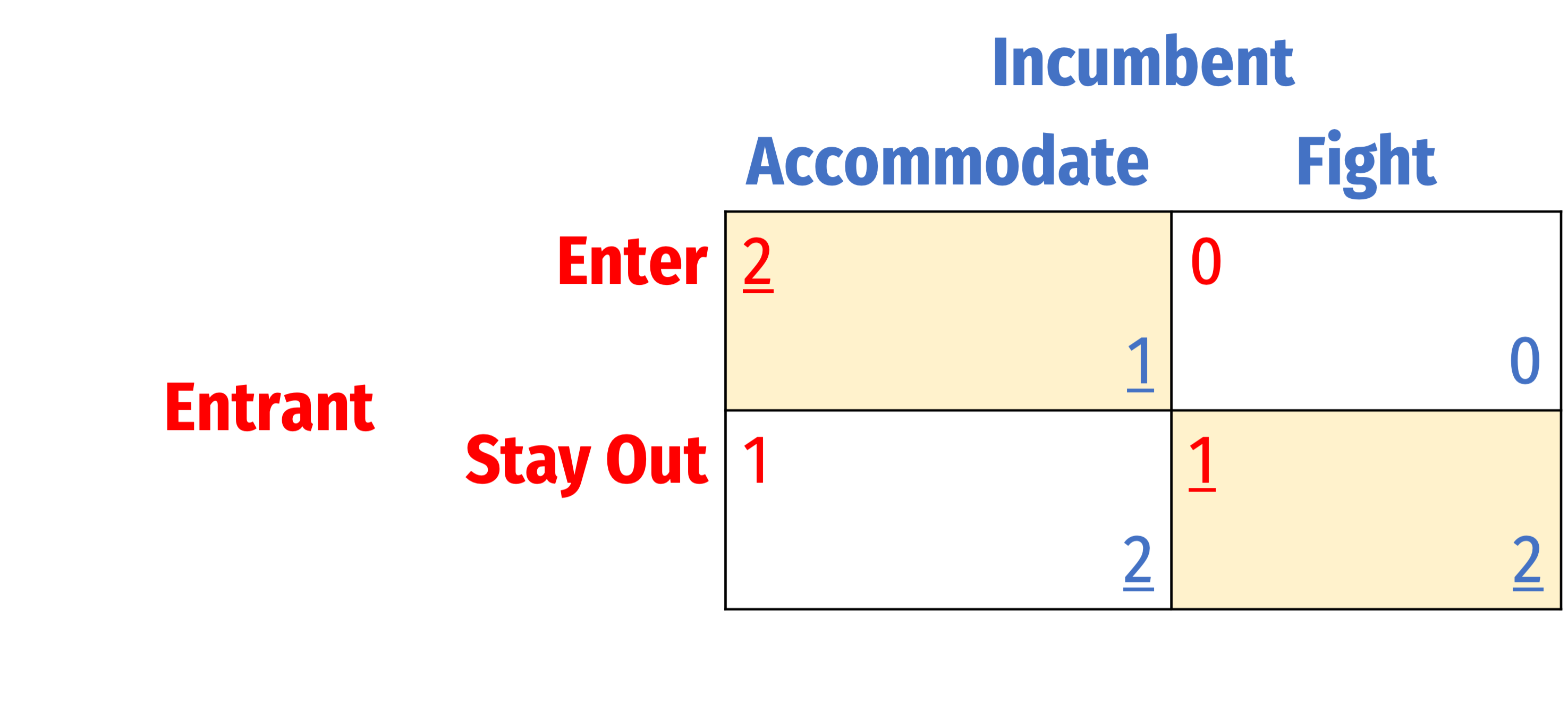
Entry Game: Normal vs. Extensive Form
Convert this game to Normal form
Note, if Entrant plays Stay Out, doesn't matter what Incumbent plays, payoffs are the same
Solve this for Nash Equilibria...

Entry Game: Normal vs. Extensive Form
- Two Nash Equilibria:
- (Enter, Accommodate)
- (Stay Out, Fight)
- But remember, we ignored the sequential nature of this game in normal form
- Which Nash equilibrium is sequentially rational?
Entry Game: Subgames
- Subgame initiated at decision node E.1 (i.e. the full game)
- Subgame initiated at decision node I.1
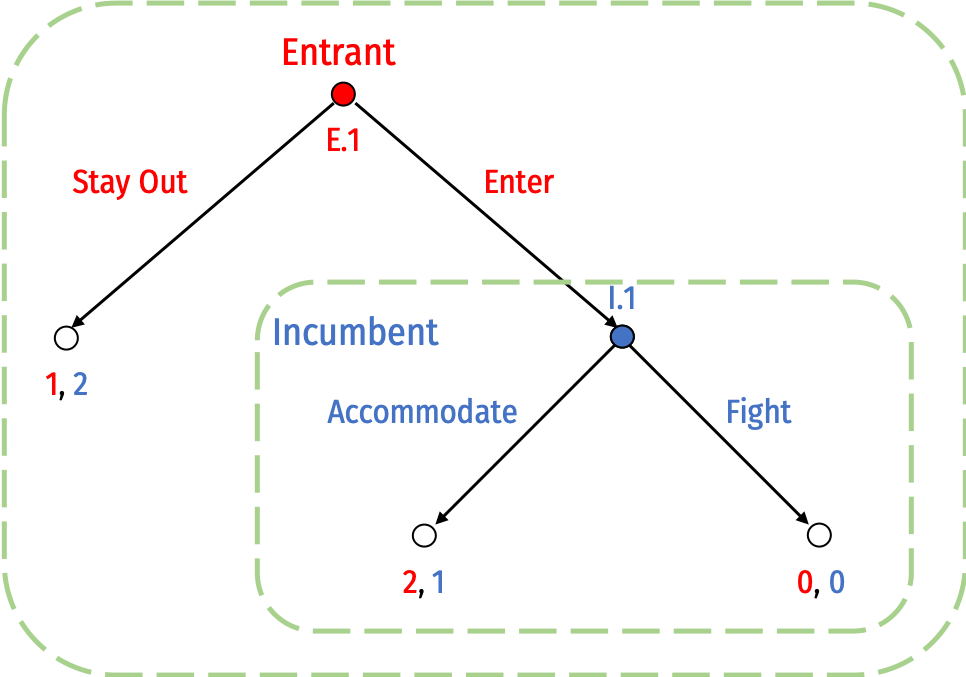
Entry Game: Subgame Perfect Nash Equilibrium
Consider each subgame as a game itself and ignore the “history” of play that got a to that subgame
- What is optimal to play in that subgame?
Consider a set of strategies that is optimal for all players in every subgame it reaches
That is a subgame perfect Nash equilibrium

Entry Game: Subgame Perfect Nash Equilibrium
- Recall our two Nash Equilibria from normal form:
- (Enter, Accommodate)
- (Stay Out, Fight)


Entry Game: Subgame Perfect Nash Equilibrium
- Recall our two Nash Equilibria from normal form:
- (Enter, Accommodate)
- (Stay Out, Fight)
Consider the second set of strategies, where Incumbent chooses to Fight at node I.1
What if for some reason, Incumbent is playing this strategy, and Entrant unexpectedly plays Enter?


Entry Game: Subgame Perfect Nash Equilibrium
It's not rational for Incumbent to play Fight if the game reaches I.1!
- Would want to switch to Accommodate!
Incumbent playing Fight at I.1 is not a Nash Equilibrium in this subgame!
Thus, Nash Equilibrium (Stay Out, Fight) is not sequentially rational
- It is still a Nash equilibrium!


Entry Game: Subgame Perfect Nash Equilibrium
Only (Enter, Accommodate) is a Subgame Perfect Nash Equilibrium (SPNE)
These strategy profiles for each player constitute a Nash equilibrium in every possible subgame!
Simple connection: rollback equilibrium is always SPNE!


Entry Game: SPNE and Credibility
- Suppose before the game started, Incumbent announced to Entrant
“if you Enter, I will Fight!”
This threat is not credible because playing Fight in response to Enter is not rational!
The strategy is not Subgame Perfect!


Strategic Moves
Strategic Moves AKA “Game Changers”
So far, assumed rules of the game are fixed
In many strategic situations, players have incentives to try to affect the rules of the game for their own benefit
- Order, available strategies, payoffs, repetition
A strategic move (“game changer”) is an action taken outside the rules an existing game by transforming it into a two-stage game
- A strategic move is made in stage I (“pre-game” move)
- A modified version of the original game is played in stage II

Types of Strategic Moves
Threats: if other players don’t choose your preferred move, you will play in a manner that will be bad for them (in second stage)
- Conditional response to other players’ actions
Promises: if other players choose your preferred move, you will play in a manner that will be good for them (in second stage)
- Conditional response to other players’ actions
Commitments: irreversibly limit your choice of action, unconditional on other players’ actions

Strategic Moves and Credibility
Key: threats and promises are often costly if you must carry them out against your own interest!
If a threat works and elicits the desired behavior in others, no need to carry it out
If a promise elicits the desired behavior in others, cost of performing the promise

Strategic Moves and Credibility
For a strategic move to work, it must be:
- observable to all players
- irreversible so that it alters other players’ expectations
Other players must believe you will actually do in the second stage what you threaten/promise you will do during the first stage
- Credibility of strategic moves open to question

Strategic Moves and Credibility
Your parents probably (tried to) used strategic moves on you
- “No dessert unless you eat your vegetables”
- “We’ll buy you a new bike if you get a B GPA”
You may have (rightly) questioned their credibility
- Most parents don’t actually want to punish or discipline their kids (it’s painful to the parents)
- (An empty) threat that changes their kid’s behavior is great, but costly if it actually has to be carried out

Non-Credibility AKA “Cheap Talk”
“Talk is cheap”
- Low cost to making promises/threats you don’t intend to carry out
Promises and threats without commitment will not change equilibrium behavior (with perfect information)
If you try to bluff in poker, and your rivals know what cards you have, they will call your bluff


Non-Credibility AKA “Cheap Talk”
Promises or threats must be incentive-compatible to work
- Threat/promise-maker must actually stand to benefit from performing the threat/promise or suffer from not performing it
In game theory terms: strategy must be subgame perfect
Subgame perfection rules out Nash equilibria relying upon non-credible threats and promises; keeps only behavior that is optimal under every circumstance!


Credible Commitment
Threats and promises can be credible with commitment
A commitment changes the game in a way that forces you to carry out your promise or threat
- tying your own hands makes you stronger!


Credible Commitment

Odysseus and the Sirens by John William Waterhouse, Scene from Homer's The Odyssey
Commitments
A commitment is an action taken unconditional on other players' actions that limits your own actions
If credible, tantamount to changing the order of the game at Stage II, so that the player making the commitment moves first
Can change outcomes of following games, since it changes other players' expectations of the consequences of their own actions

Simple Commitment Example in Chicken
Take the game of Chicken
Both players want to act tough from the beginning and project an image that they'll never back down, so the other player must
But what makes a credible commitment?

Simple Commitment Example in Chicken
Only a visible and irreversible action commits Row to going straight is credible
- rip out steering wheel
- tie the steering wheel
Forces Column to Swerve
