4.5 — Bayesian Players
ECON 316 • Game Theory • Fall 2021
Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/gameF21
gameF21.classes.ryansafner.com
Bayesian Statistics
Bayesian Statistics
Most people’s understanding & intuitions of probability are about the objective frequency of events occurring
- “If I flip a fair coin many times, the probability of Heads is 0.50”
- “If this election were repeated many times, the probability of Biden winning is 0.60”
This is known as the “frequentist” interpretation of probability
- And is almost entirely the only thing taught to students (because it’s easier to explain)

Bayesian Statistics
Another valid (competing) interpretation is probability represents our subjective belief about an event
- “I am 50% certain the next coin flip will be Heads”
- “I am 60% certain that Biden will win the election”
- This is particularly useful for unique events (that occur once...and really, isn’t that every event in the real world?)
This is known as the “Bayesian” interpretation of probability

Bayesian Statistics
In Bayesian statistics, probability measures the degree of certainty about an event
- Beliefs range from impossible (p=0) to certain (p=1)
This conditions probability on your beliefs about an event

Rev. Thomas Bayes
1702—1761
Bayesian Statistics
The bread and butter of thinking like a Bayesian is updating your beliefs in response to new evidence
- You have some prior belief about something
- New evidence should update your belief (level of certainty) about it
- Updated belief known as your posterior belief
Your beliefs are not completelydetermined by the latest evidence, new evidence just slightly changes your beliefs, proportionate to how compelling the evidence is
This is fundamental to modern science and having rational beliefs
- And some mathematicians will tell you, the proper use of statistics

Bayesian Statistics Examples
You are a bartender. If the next person that walks in is wearing a kilt, what is the probability s/he wants to order Scotch?
You are playing poker and the player before you raises.
What is the probability that someone has watched the Superbowl? What if you learn that person is a man?
You are a policymaker deciding foreign policy, and get a new intelligence report.
You are trying to buy a home and make an offer, which the seller declines.


Conditional Probability
- All of this revolves around conditional probability: the probability of some event B occurring, given that event A has already occurred
P(B|A)=P(A and B)P(A)
- P(B|A): “Probability of B given A”

Conditional Probability
- All of this revolves around conditional probability: the probability of some event B occurring, given that event A has already occurred
P(B|A)=P(A and B)P(A)
- If we know A has occurred, P(A)>0, and then every outcome that is ¬A (“not A”) cannot occur (P(¬A)=0)
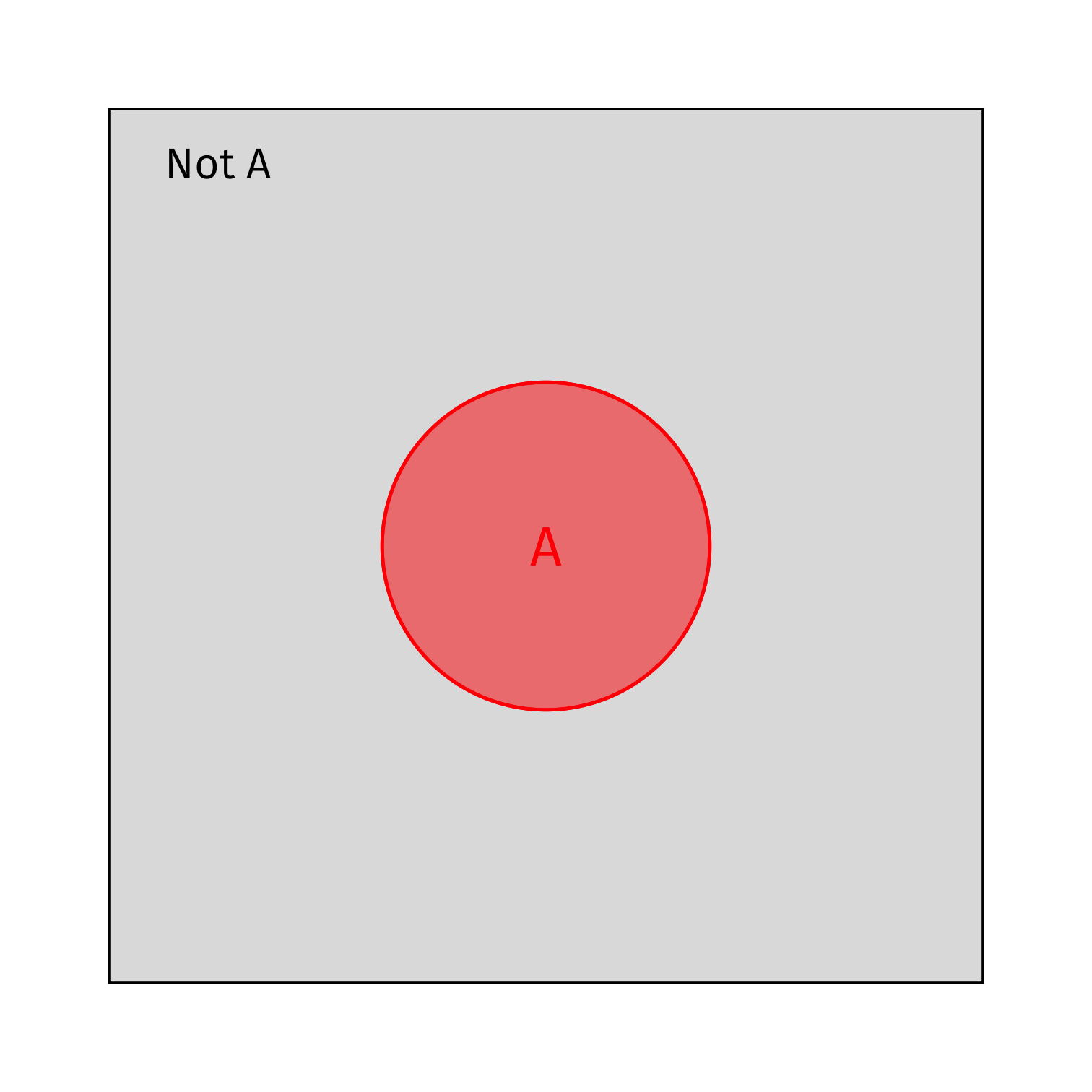
Conditional Probability
- All of this revolves around conditional probability: the probability of some event B occurring, given that event A has already occurred
P(B|A)=P(A and B)P(A)
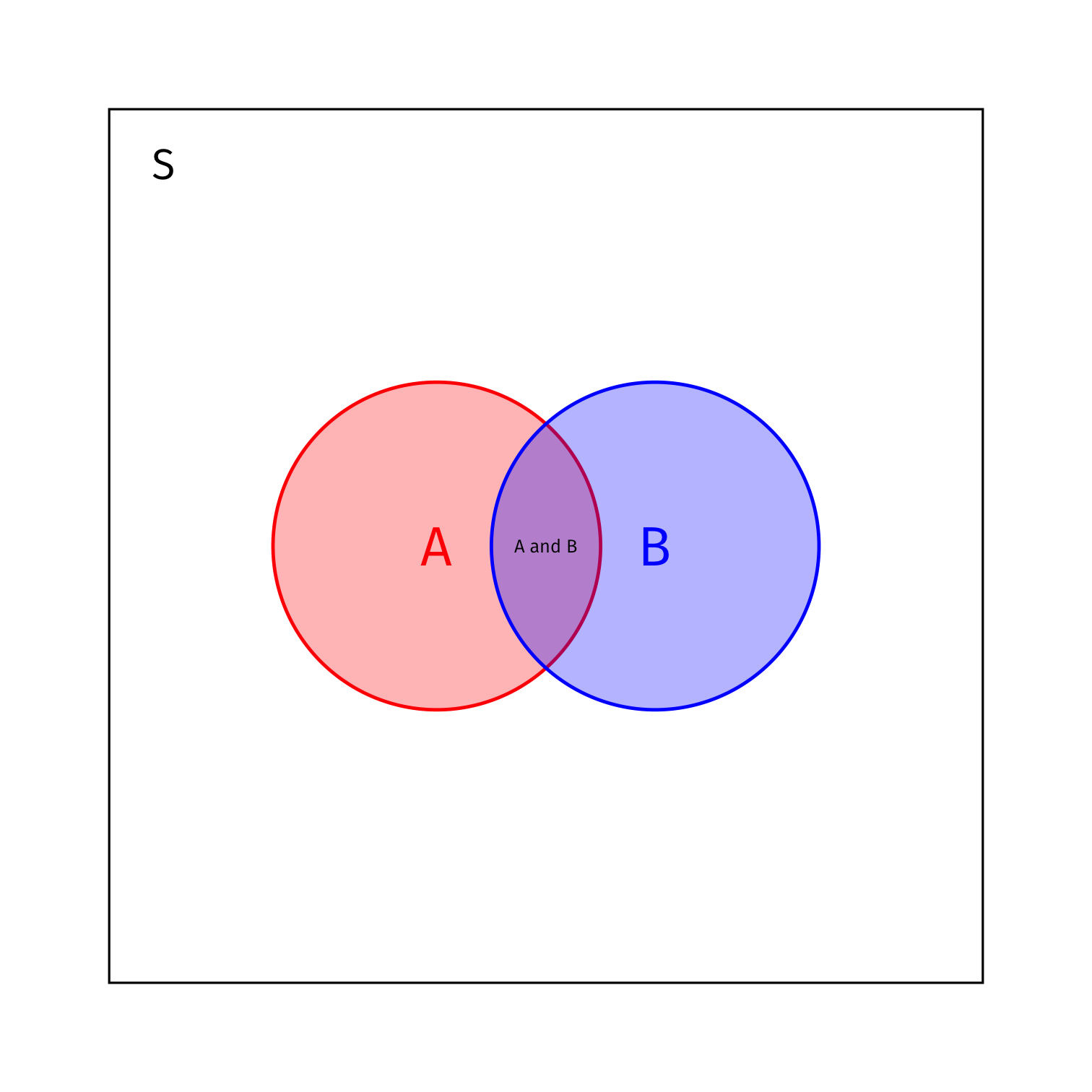
Conditional Probability
- All of this revolves around conditional probability: the probability of some event B occurring, given that event A has already occurred
P(B|A)=P(A and B)P(A)
- If we know A has occurred, P(A)>0, and then every outcome that is ¬A (“not A”) cannot occur (P(¬A)=0)
- The only part of B which can occur if A has occurred is A and B
- Since the sample space S must equal 1, we’ve reduced the sample space to A, so we must rescale by 1P(A)

Conditional Probability
P(B|A)=P(A and B)P(A)
- If events A and B were independent, then the probability P(A and B) happening would be just P(A)×P(B)
- P(A|B)=P(A)
- P(B|A)=P(B)

Conditional Probability
P(B|A)=P(A and B)P(A)
- But if they are not independent, it’s P(A and B)=P(A)×P(B|A)
- (Just multiplying both sides above by the denominator, P(A))
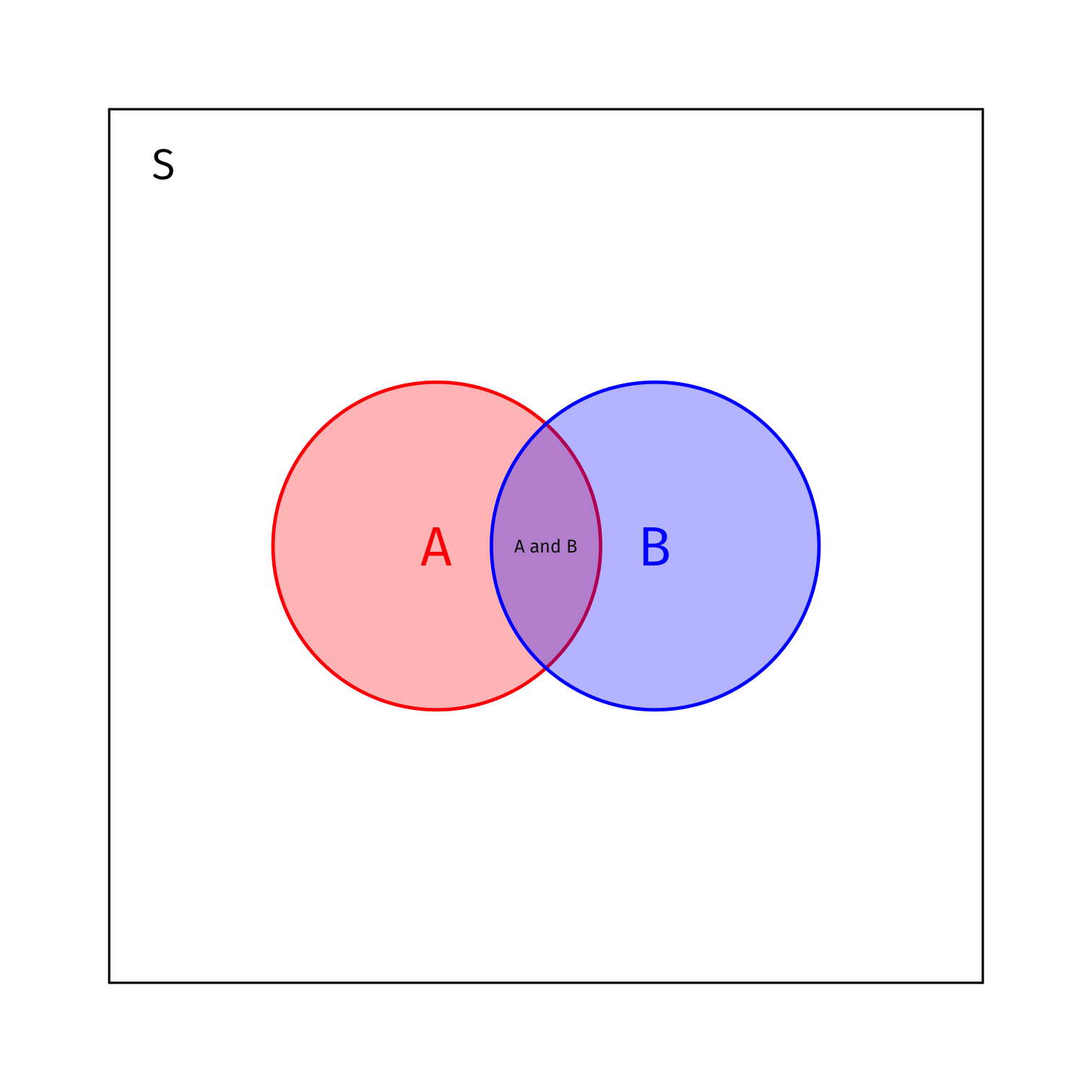
Conditional Probability and Bayes’ Rule
- Bayes realized that the conditional probabilities of two non-independent events are proportionately related
P(B|A)=P(A and B)P(A)
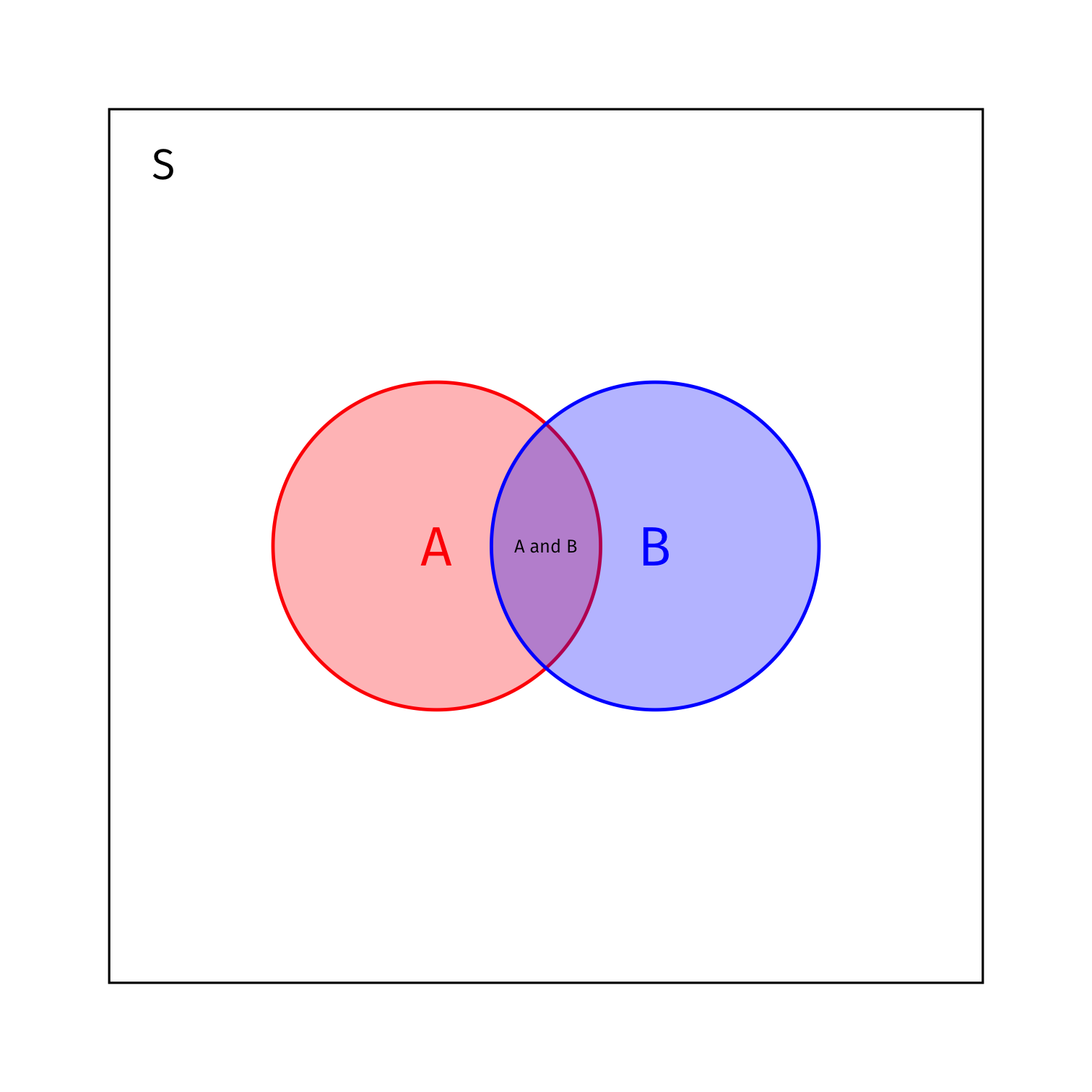
Conditional Probability and Bayes’ Rule
- Bayes realized that the conditional probabilities of two non-independent events are proportionately related
P(B|A)=P(A and B)P(A)
P(A|B)P(B)=P(A and B)=P(B|A)P(A)
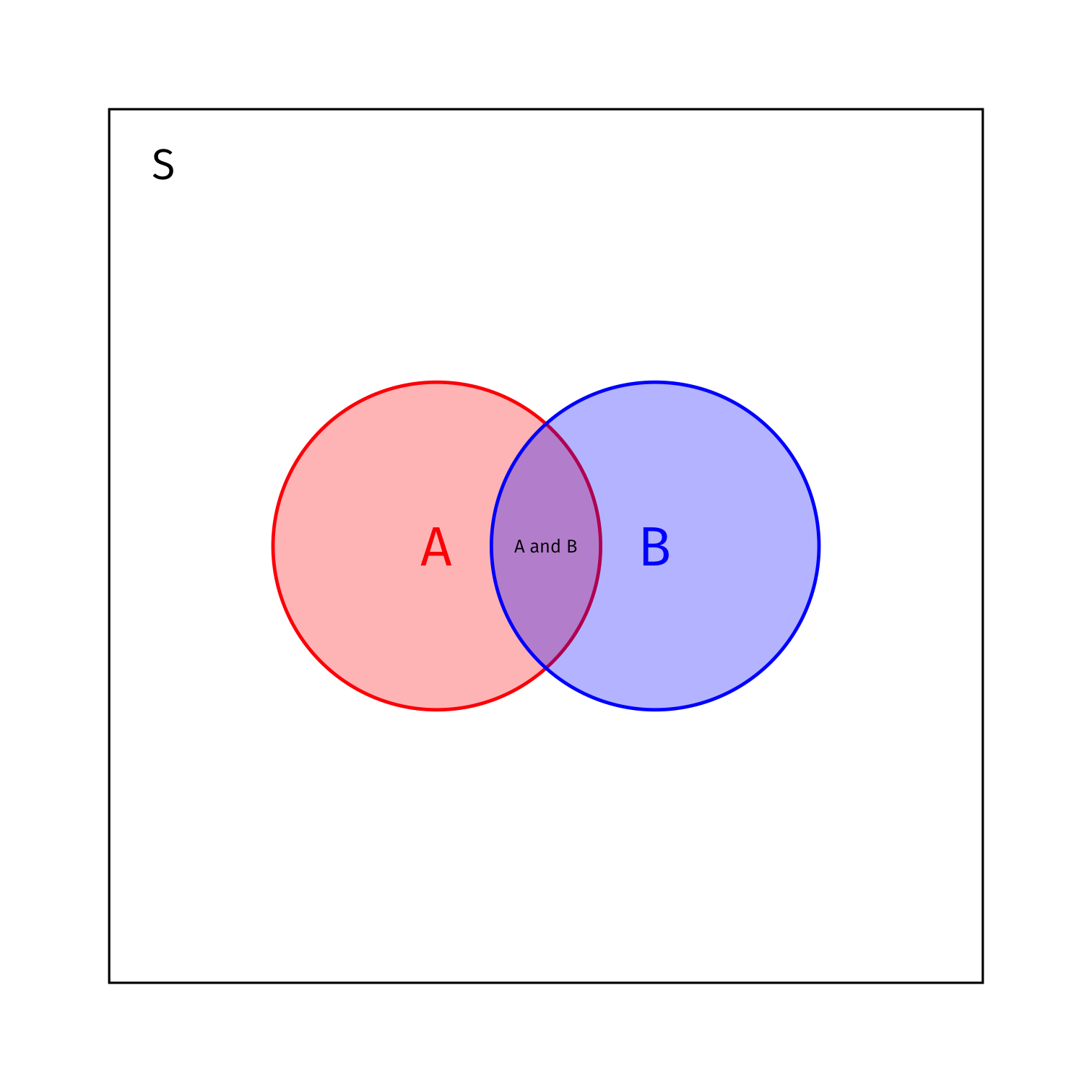
Conditional Probability and Bayes’ Rule
- Bayes realized that the conditional probabilities of two non-independent events are proportionately related
P(B|A)=P(A and B)P(A)
P(A|B)P(B)=P(A and B)=P(B|A)P(A)
- Divide everything by P(B), you get, famously, Bayes’ rule:
P(A|B)=P(B|A)P(A)P(B)

Bayes’ Rule: Hypotheses and Evidence
The A’s and B’s are rather difficult to remember if you don’t use this often
A lot of people prefer to think of Bayes’ rule in terms of a hypothesis you have (H), and new evidence or data e
P(H|e)=P(e|H)p(H)P(e)
- P(H|e): posterior your hypothesis is correct given the new evidence
- P(e|H): likelihood of seeing the evidence under your hypothesis
- P(H): prior belief in of your hypothesis
- P(e): average likelihood of seeing the evidence under any/all hypothesis

Bayes’ Rule Example
Bayes’ Rule Example
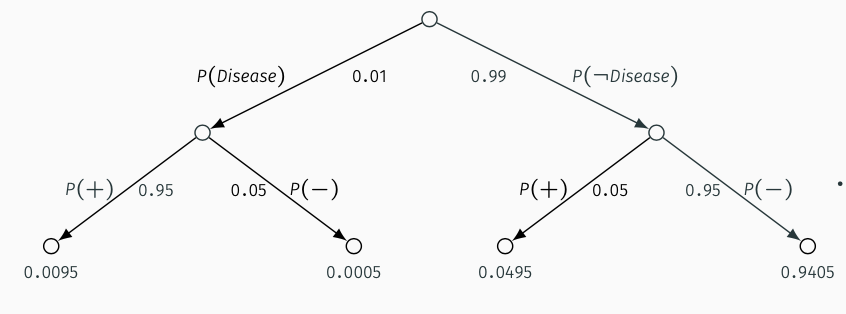
Example: Suppose 1% of the population has a rare disease. A test that can diagnose the disease is 95% accurate. What is the probability that a person who takes the test and comes back positive has the disease?
- What would you guess the probability is?
Bayes’ Rule Example
Example: Suppose 1% of the population has a rare disease. A test that can diagnose the disease is 95% accurate. What is the probability that a person who takes the test and comes back positive has the disease?
P(Disease)=0.01
P(+|Disease)=0.95=P(−|¬Disease)
We know P(+|Disease) but want to know P(Disease|+)
- These are not the same thing!
- Related by Bayes’ Rule:
P(Disease|+)=P(+|Disease)P(Disease)P(+)

Bayes’ Rule Example
- P(Disease)=0.01
- P(+|Disease)=0.95=P(−|¬Disease)
P(Disease|+)=P(+|Disease)P(Disease)P(+)
- What is P(+)??

Bayes’ Rule Example
- What is the total probability of B in the diagram?
P(B)=P(B and A)+P(B and ¬A)=P(B|A)P(A)+P(B|¬A)P(¬A)
- This is known as the law of total probability
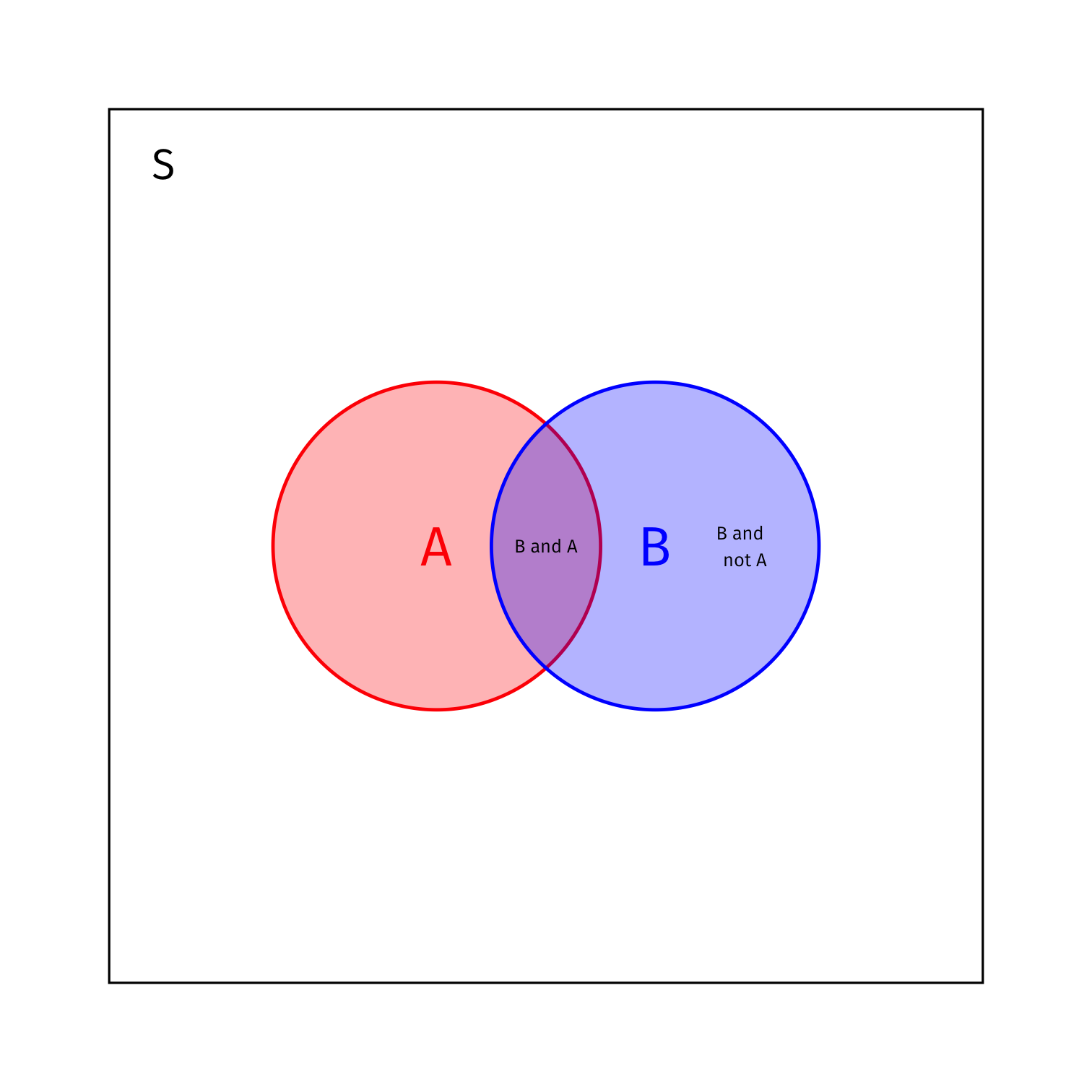
Bayes’ Rule Example: Aside
- Because we usually have to figure out P(B) (the denominator), Bayes’ rule is often expanded to
P(B|A)=P(A|B)P(A)P(B|A)P(A)+P(B|¬A)P(¬A)
- Assuming there are two possibilities (A and ¬A), e.g. True or False
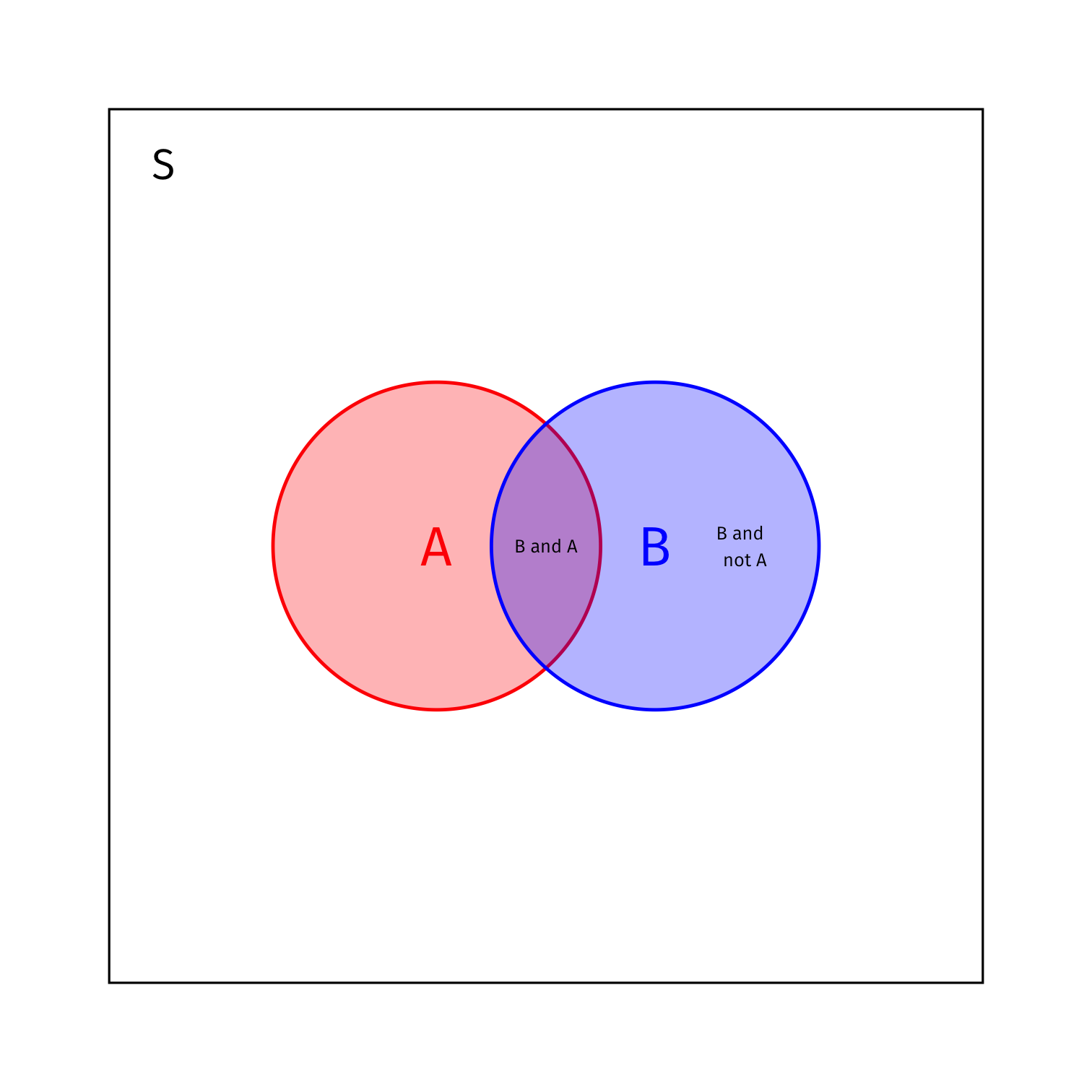
Bayes’ Rule Example: Aside
- If there are more than two possibilities, you can further expand it to n∑i=1P(B|Ai)P(Ai) for n number of possible alternatives to A
Bayes’ Rule Example
- What is the total probability of +?
P(+)=P(+ and Disease)+P(+ and ¬ Disease)=P(+|Disease)P(Disease)+P(+|¬Disease)P(¬Disease)
- P(Disease)=0.01
- P(+|Disease)=0.95
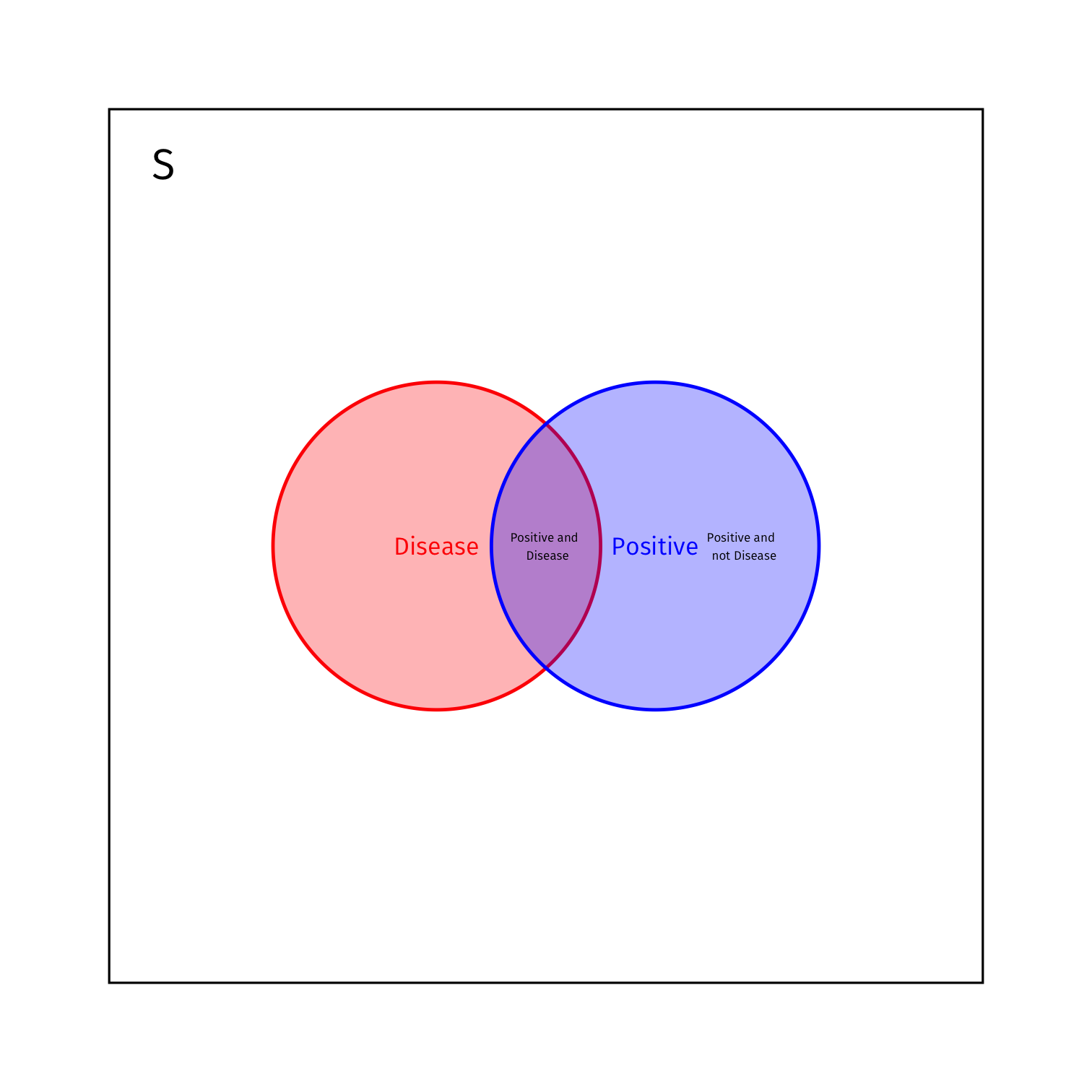
Bayes’ Rule Example
- What is the total probability of +?
P(+)=P(+ and Disease)+P(+ and ¬ Disease)=P(+|Disease)P(Disease)+P(+|¬Disease)P(¬Disease)
- P(Disease)=0.01
- P(+|Disease)=0.95
P(+)=0.95(0.01)+0.05(0.99)=0.0590
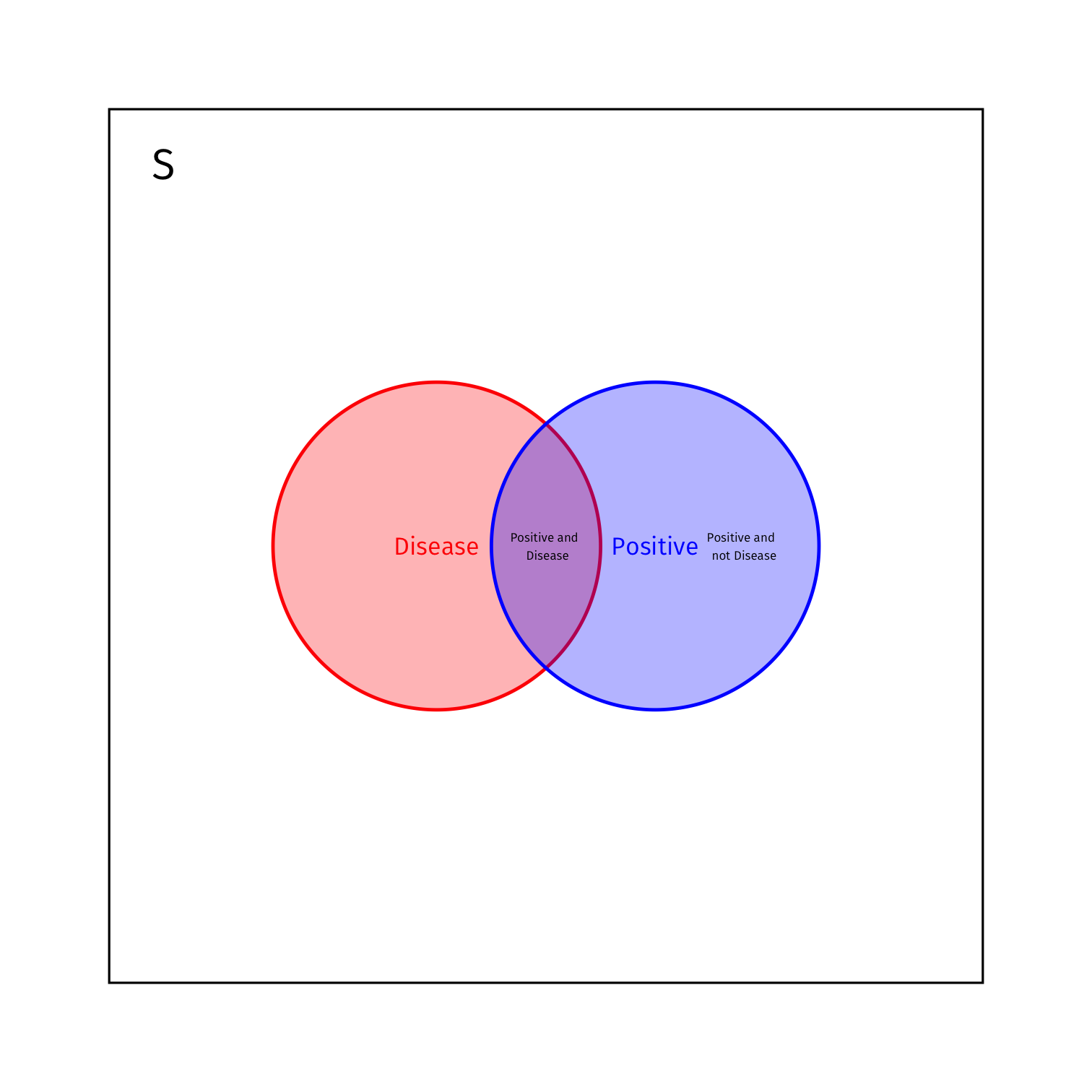
Bayes’ Rule Example
| Disease | ¬ Disease | Total | |
|---|---|---|---|
| + | 0.0095 | 0.0495 | 0.0590 |
| - | 0.0005 | 0.9405 | 0.9410 |
| Total | 0.0100 | 0.9900 | 1.0000 |
Bayes’ Rule Example
- P(Disease)=0.01
- P(+|Disease)=0.95=P(−|¬Disease)=0.95
- P(+)=0.0590

Bayes’ Rule Example
- P(Disease)=0.01
- P(+|Disease)=0.95=P(−|¬Disease)=0.95
- P(+)=0.0590
P(Disease|+)=P(+|Disease)P(Disease)P(+)

Bayes’ Rule Example
- P(Disease)=0.01
- P(+|Disease)=0.95=P(−|¬Disease)=0.95
- P(+)=0.0590
P(Disease|+)=P(+|Disease)P(Disease)P(+)P(Disease|+)=0.95×0.010.0590=0.16
- The probability you have the disease is only 16%!
- Most people vastly overestimate because they forget the base rate of the disease, P(Disease) is so low (1%)!

Bayes’ Rule and Bayesian Updating
- Bayes Rule tells us how we should update our beliefs given new evidence

