Please read the instructions for completing homeworks.
Concepts
Question 1
Explain, in your own words, what a strategy means in (sequential) games.
Question 2
Draw a simple game tree between two players (come up with any simple scenario, even an abstract one). Define, and indicate on the tree:
- The root node
- Decision nodes
- Terminal nodes
- Decisions available to each player
- Payoffs for each player
- Strategies available to each player
Problems
Question 3
In an alternate version of the Century Mark game we played in class, two players take turns choosing a number between 1—10 (inclusive) to add to the count (starting at 0). The first player to bring the count to 100 loses this game.
Describe Player 2’s optimal strategy, and fully describe your reasoning. Does this game have a first-mover advantage or a second-mover advantage?
Question 4
Suppose two players, Hansel and Gretel, play a sequential-move game. Hansel moves first, Gretel moves second, and each player moves only once.
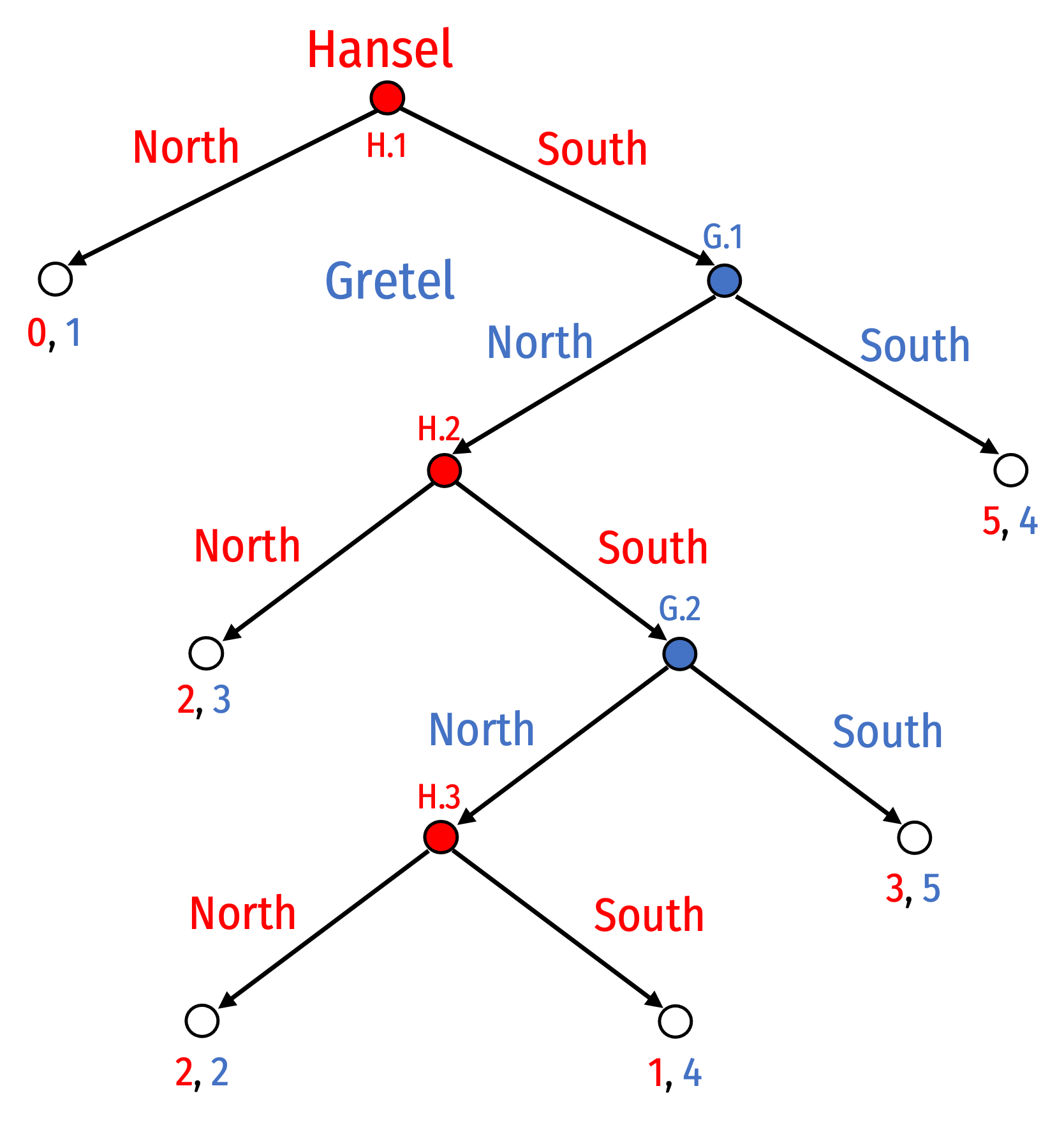
Part A
List all of Hansel’s possible strategies.
Part B
List all of Gretel’s possible strategies.
Part C
Using backward induction, find is the Rollback equilibrium. Prune the branches on the game tree as you are doing so. What strategy is each player playing in equilibrium?
Question 5
Suppose Airbus and Boeing are rival companies seeking to develop a new commercial jetliner. Suppose Boeing is ahead in the development process and Airbus is considering whether to enter the market. If Airbus stays out, it earns 0 profit, whereas Boeing enjoys a monopoly and earns a profit of $1 billion. If Airbus enters, Boeing must decide whether to accommodate Airbus peaceably or to wage a price war. In the event of peaceful competition, each firm would earn a profit of $300 million. If there is a price war, each will lose $100 million since they will push the price lower than the development costs.
Part A
Draw this game in extensive form.
Part B
List all of Airbus’ possible strategies.
Part C
List all of Boeing’s pure strategies.
Part D
Using backward induction, find is the Rollback equilibrium. Prune the branches on the game tree as you are doing so. What strategy is each firm playing in equilibrium?
Question 6
The game tree below shows a game between an Inventor and a potential Copycat under existing patent law.
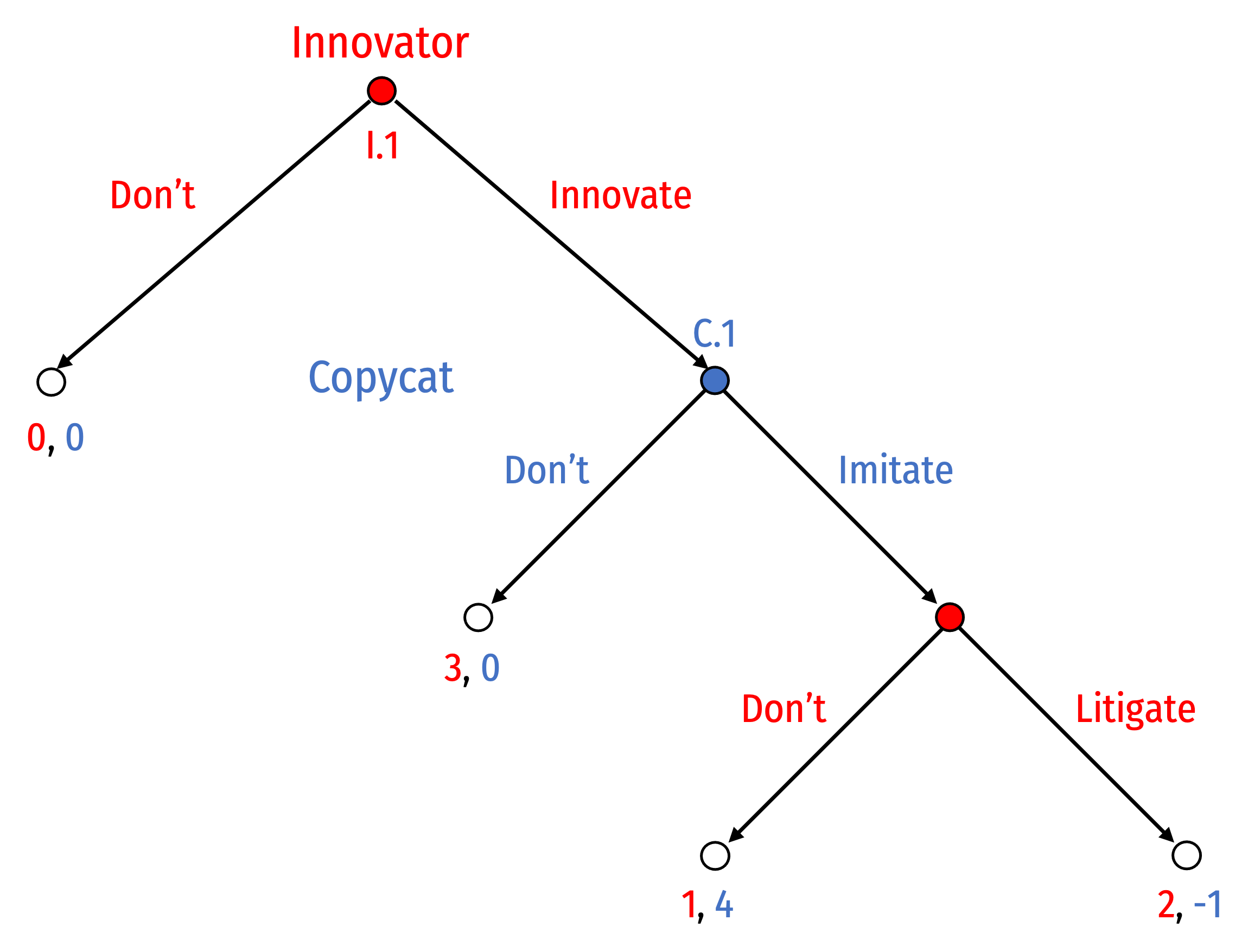
Part A
List all of Inventor’s possible strategies.
Part B
List all of Copycat’s possible strategies.
Part C
Using backward induction, find is the Rollback equilibrium. Prune the branches on the game tree as you are doing so. What strategy is each player playing in equilibrium?
Part D
Suppose patent litigation has become prohibitively expensive, lowering Inventor’s litigation payoff to \(0.5\). Solve for the new Rollback equilibrium (state it below), and draw a new tree, pruning the branches.
Question 7
Two distinct bills, \(A\) and \(B\), are being debated in Washington. Congress prefers proposal A, and the president prefers proposal \(B\), but both would prefer something gets passed, and both would suffer the most if nothing gets passed. The proposals are not mutually exclusive; either, both, neither proposal may become law. Thus, there are four possible outcomes, and the payoffs to the two parties are as follows (a larger number represents a higher payoff):
| Outcome | Congress | President |
|---|---|---|
| A becomes law | 4 | 1 |
| B becomes law | 1 | 4 |
| Both become law | 3 | 3 |
| Neither become law | 2 | 2 |
Part A
Draw a game tree as follows: first Congress can pass a bill that can contain A, B, or both A & B, or pass nothing at all. If no bill is passed, the game ends. If any bill is passed, the president decides to sign or veto the bill. Congress does not have enough votes to override a veto, so the game ends with the bill becoming a law if the president signs.
Part B
Solve for the rollback equilibrium (state it below), and prune the branches on the tree above. What strategy is Congress playing, and is the president playing in equilibrium?
Part C
Now suppose the rules of the game are changed in only one respect: the president is given the extra power of a Line-Item Veto. Thus, if Congress passes a bill containing both A and B, the president may choose not only to sign or veto the bill as a whole, but also to veto just one of the two proposals. Redraw the new tree and find the rollback equilibrium.
Part D
Compare the results of the equilibrium without the Line Item Veto and with the Line Item Veto. Explain intuitively the logic behind the difference.