Problem Set 5

Due on Monday November 22.

Please read the instructions for completing homeworks.

Concepts

Question 1

What is the difference between a finitely repeated game and an infinitely repeated game? What is the pure strategy Nash equilibrium in a finitely-repeated game (with a unique Nash equilibrium in a one-shot version)? Describe two interpretations of infinitely repeated games.

Question 2

Describe, in your own words, the simple version (or implications) of the folk theorem for sustaining cooperation.

Question 3

Describe what a subgame means, and circle all subgames in the following game tree.

Question 4

Define subgame perfect Nash equilibrium.

Question 5

Explain what strategic moves are, and explain the three major types of strategic moves.

Question 6

What makes a promise credible? What makes a threat credible? Give some examples of each, and in your answers, use the concept of subgame perfection.

Question 7

What makes a strategy evolutionarily stable (ESS)? Describe the difference between monomorphic and polymorphic equilibria.

Problems

Question 8

Consider an evolutionary version of the Stag Hunt game, where members of a species can decide to cooperate and hunt a Stag together, or defect and go after a Hare on their own.

Part A

Is Stag an evolutionarily stable strategy (ESS)?

Part B

Is Hare an evolutionarily stable strategy (ESS)?

Part C

What are the pure strategy Nash equilibria (PSNE) of this game? Reconcile this with your answers in parts a and b.

Part D

Suppose the environment changes such that hunting a large Hare alone is equally rewarding to the cooperative hunt of a Stag (but if they both hunt Hare, it is less rewarding).

Under the new environment, is Hare evolutionarily stable (ESS)?

Part E

Under the new environment, is Stag evolutionarily stable (ESS)?

Part F

Given what we learned in class about the relationship between (pure strategy) Nash equilibria and evolutionarily stable strategies, we now need a new refinement. Define a strict Nash equilibrium in pure strategies to mean that each player is playing a strict (or unique) best response to other players, i.e. there is no other strategy that is also a best response to another player. In the one-shot game in part d, which PSNE are strict, and which are not (i.e. “weak” PSNE? What do you then think is the relationship between ESS and strict/non-strict PSNE?

Question 9

Consider the evolutionary Hawk-Dove game, where members of a species are competing over a resource valued at 12, with a cost of losing a fight being $- 15$ .

Part A

Draw the payoff matrix for the game.

Part B

Find the pure strategy Nash equilibria.

Part C

Is Hawk evolutionarily stable?

Part D

Is Dove evolutionarily stable?

Part E

Reconcile your answers in parts c and d to your answer in part b.

Part F

Find the evolutionarily stable (polymorphic) equilibrium distribution of Hawks and Doves. [Hint: let $p$ be the probability the other player is a Hawk.]

Question 10

Consider the following game between two roommates. Roommate A has a very difficult exam the next morning, while Roommate B does not. The two of them can each decide to Study or Go Out that evening. Both would rather do something together, while A would certainly prefer they both Study and B would prefer they both Go Out.

Part A

Suppose they both agree that A gets to decide first and B must respond, as in the following game:

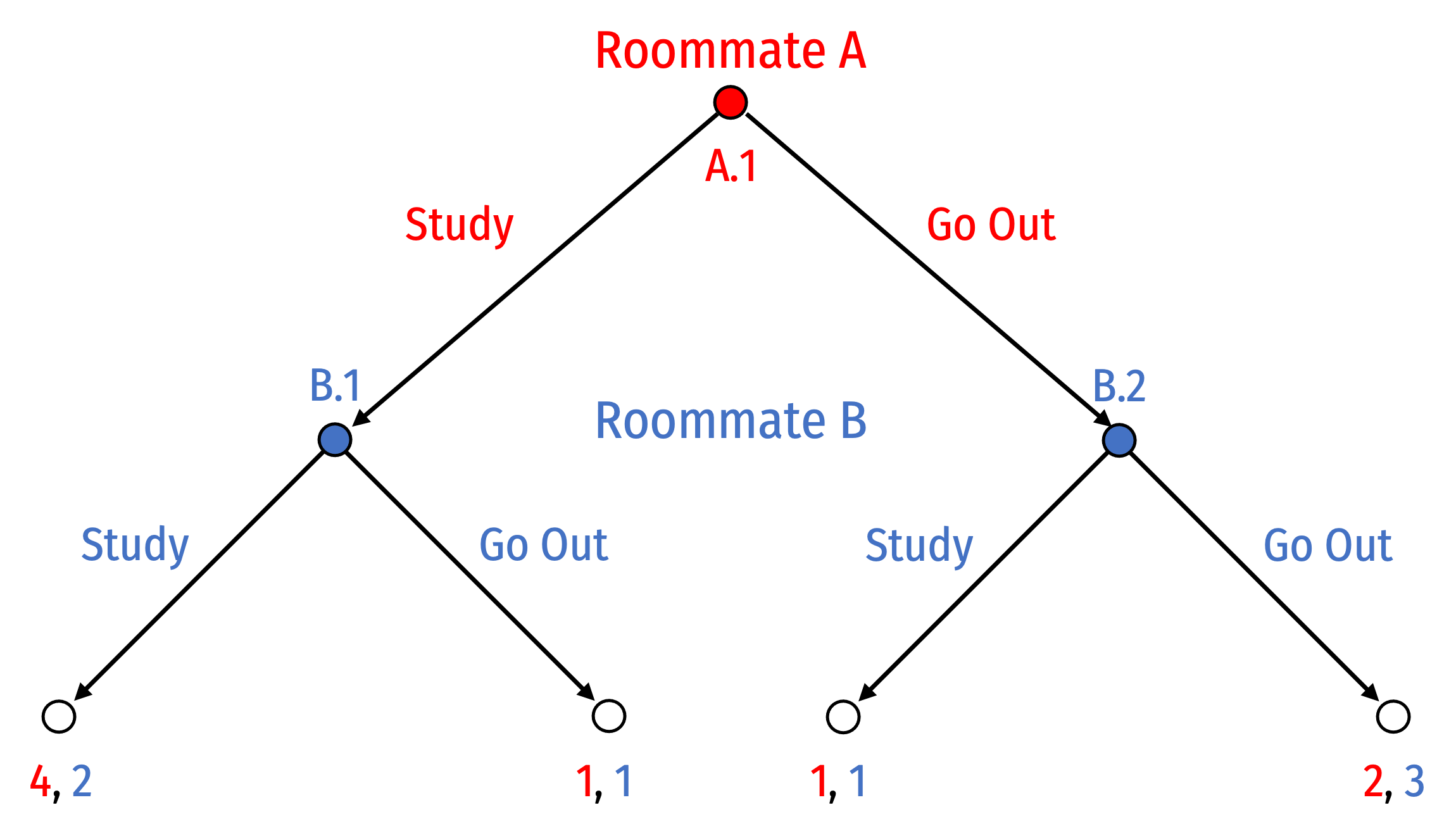
Solve this game for the rollback equilibrium using backwards induction.

Part B

Circle all subgames on the game tree.

Part C

Carefully convert this game from extensive form to strategic form. (Be mindful of how many potential strategies each player has!) Then, find any Nash equilibria in strategic form.

Part D

Which Nash equilibrium is subgame perfect? Why?

Part E

Suppose in an attempt to get A to Go Out, B says they will Go Out regardless of what A does. If A still gets to decide first (i.e. it is the same game as in part a), what should A make of this?

Last updated on Nov 24, 2021