Problem Set 4

Due on Wednesday October 6.

Please read the instructions for completing homeworks.

Concepts

Question 1

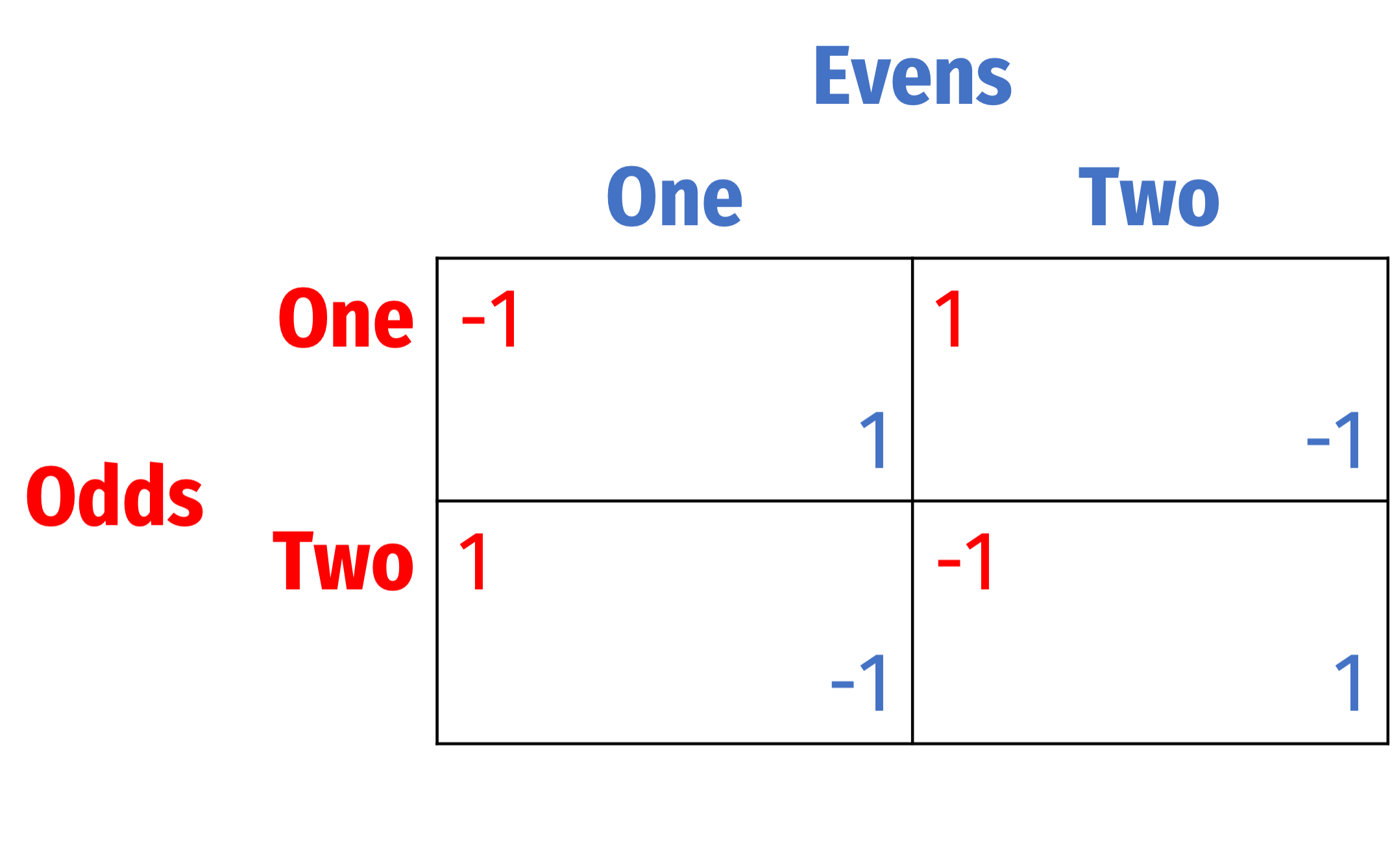
Consider the simple hand game of “odds and evens,” where two players simultaneously hold out one or two of their fingers, and add up the sum. Suppose Player 1 has chosen Odds, and Player 2 has chosen Evens, such that the sum is odd, Player 1 wins; if the sum is even, Player 2 wins. Let a win be a payoff of 1, and a loss be a payoff of \(-1\). The payoff table is below:

Part A

Find any pure strategy Nash equilibria (PSNE).

Part B

Let p be the probability Odds plays One. Write out Evens’ expected payoffs of playing One and playing Two given this.

Part C

Solve for the optimal value of p that makes Evens indifferent between playing One and playing Two.

Part D

Let q be the probability Evens plays One. Write out Odds’ expected payoffs of playing One and playing Two given this.

Part E

Solve for the optimal value of q that makes Odds indifferent between playing One and playing Two.

Part F

What is the mixed strategy Nash equilibrium (MSNE) of this game?

Part G

What is each player’s expected payoff in MSNE?

Question 2

You and your friend are deciding on a place to go for dinner, but are too busy to call or text one another. Each of you can go to the Chinese Restaurant or the Italian Restaurant – suppose you prefer Chinese and your friend prefers Italian.

Part A

Find any pure strategy Nash equilibria (PSNE).

Part B

Let p be the probability You go to the Chinese restaurant. Write out your Friend’ expected payoffs of going to the Chinese and to the Italian restaurant given this.

Part C

Solve for the optimal value of p that makes your Friend indifferent between going to the Chinese and to the Italian restaurant.

Part D

Let q be the probability your Friend goes to the Chinese restaurant. Write out Your’ expected payoffs of going to the Chinse and to the Italian restaurant given this.

Part E

Solve for the optimal value of q that makes You indifferent between going to the Chinese and to the Italian restaurant.

Part F

What is the mixed strategy Nash equilibrium (MSNE) of this game?

Part G

What is each player’s expected payoff in MSNE?

Part H

Write out and draw each player’s best response function. Put \(p\) on the horizontal axis and \(q\) on the vertical axis. Label all equilibria appropriately. Label all equilibria on your graph. Hint: which expected payoff of your Friend’s strategies increases as \(p\) increases (decreases)? Which expected payoff of Your strategies increases as \(q\) increases (decreases)?

Part I

Given your answers to the above questions, calculate the probability that both of you go to the Chinese restaurant and the probability that both of you go to the Italian restaurant. Hint: assume each person’s choice is independent.

Question 3

The chief of police is attempting to crack down on drunk driving, and is deciding whether to set up a sobriety checkpoint. Setting up a checkpoint always catches drunk driving, but costs the city resources. A partygoer can choose to drink Beer or Soda before driving home. Suppose the payoffs are as follows:

Part A

Find the mixed strategy Nash equilibrium.

Part B

What is each party’s expected value under the MSNE?

Last updated on Oct 15, 2021